bandit-based and multi-fidelity methods
MFES-HB
bohb或者hyperband在不同的bracket的内部sh过程中会产生非常多各种精度下验证的结果(即不同的 $r_i$),我们可以将这些不同的精度、验证的配置及对应的结果保存下来,并根据精度的不同分为 $K$ 组:$D_1, \dots, D_K$,并且从hyperband一文我们可以知道这里 $K$ 和单轮最大资源 $R$ 的关系是:
$$
K = \lfloor log_{\eta}(R) \rfloor + 1
$$
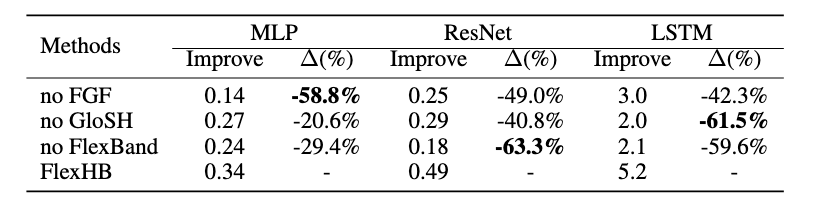
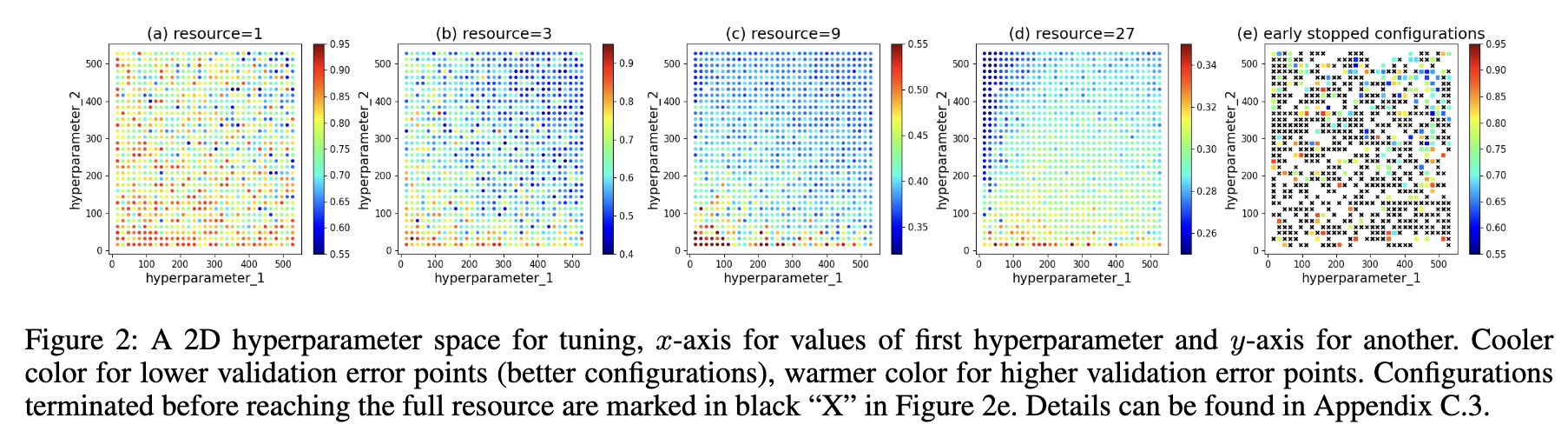
然后我们还可以知道的是高精度下对目标函数 $f$ 的验证结果是unbiased的,与之相反低精度的验证结果 $D_i(i = 1 \to K-1)$ 是biased的。所以之前的方法比如bohb和hyperband的做法是直接抛弃了所有低精度的验证结果,用高精度即 $r_{K}= R$ 下的测量结果来训练代理模型 $M_K$,并直接将 $M_K$ 作为最终的模型。但mfes-hb认为虽然使用每个低精度结果拟合出来的 $f^{1: K-1}$ 和高精度没有偏置的拟合 $f^K$ 有些差距和不同,但他们之间其实存在着一些关系,所以我们可以将这部分低精度的结果利用起来。这里的关系具体是说,随着精度增加,越接近全精度,产生的验证结果拟合的目标函数就越接近真正的 $f$,如下面四张图,图中黄色的部分是指在验证集上的错误率低的那些较好的配置,我们可以看到从左到右随着精度的不短增加,这部分黄色的区域是在逐步向没有偏置的结果接近的。
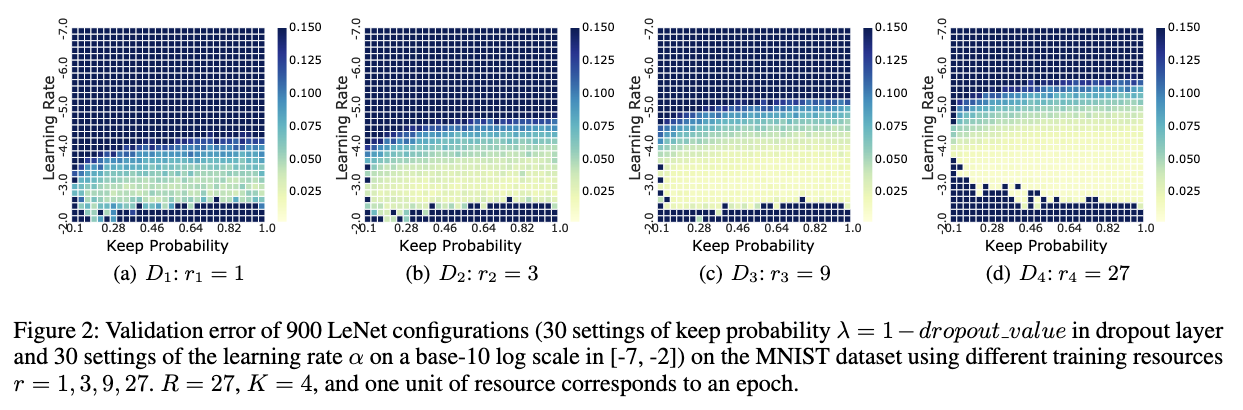
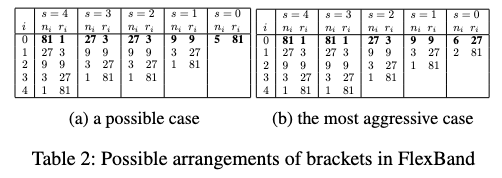
此外,由于sh策略的特性,随着精度的增加,验证配置的数量减少。即对于 $D_i$,若其验证的配置数量为 $N_i = \vert D_i \vert$,我们可以得到 $N_1 > N_2 > \dots > N_K$。对于下面这张表,有精度 $r_i = { 1, 3, 9, 27, 81 }$,$N_i = { 81, 54, 27, 15, 10 }$。
因此,高精度验证结果的数量比较少,是不足以拟合模型的。所以作者认为说可以综合高精度和低精度的结果来拟合最终的模型。
首先要做的是就是对各组精度的结果进行normalize。然后对每个精度组都单独拟合一个模型 $M_i$,最后的集成代理模型 $M_{ens}$ 是这些模型的加权,基础模型 $M_i$ 的权重为 $w_i \in [0, 1]$ 并且 $\sum^{K}_{i = 1}w_i = 1$,这里的权重反应了当前精度 $r_i$ 对集成代理模型的贡献。
还有一个问题,上面阐述过每个基础模型之间并不是独立的,那么我们就不能粗暴地用每个基础模型的均值和方差进行加和或者平方和来计算集成代理模型的均值和方差。所以这里引入了如下公式(gPoE)来计算:
$$
\mu_{ens}(\mathcal{x}) = (\sum\limits_{i}\mu_i(\mathcal{x})w_i \sigma_{i}^{-2}(\mathcal{x})) \sigma^2_{ens}(\mathcal{x})\
\sigma^2_{ens}(\mathcal{x}) = (\sum\limits_{i}w_i \sigma_{i}^{-2}(\mathcal{x}))^{-1}
$$
下一个问题是,我们到底应该如何去计算每个基础模型的权重,直觉上这个权重的值应该和这个基础模型最最终 $f$ 的近似程度成正比。所以呢一个可行的方法是使用 pairwise ranking loss,也就是说我们并不关心配置验证得到的均方误差,我们只关心每个配置之间的排名关系。其定义如下:
$$
\mathcal{L}(M_i) = \sum \limits ^{N_K} _{j = 1} \sum \limits ^{N_K} _{k = 1} \mathbb{1}((\mu _i(\mathcal{x _j}) < \mu _i(\mathcal{x _k})) \oplus (y _j < y _k))
$$
这个公式是什么意思,它表示基于模型预测和真实值排序关系不一致的成对数量,其实就是计算:对于精度 $r_i$,其验证结果集合 $D_i$ 里,两两配置预测和真实值大小关系不一致的数量,统计出来,对每个低精度的都这样的统计。这里的真实值就是配置在高精度下跑出来的值,预测值则是这个配置曾经在低精度下跑出来的结果。
然后呢利用这个不一致数量来计算一致比例 $p_i$,就是1减去不一致的比例:
$$
p_i = 1 - \frac{\mathcal{L}(M_i; D_K)}{N_{pairs}} \
N_{pairs} = C^{2}{\vert D_K \vert}
$$
然后计算权重,这里的意思就是每个模型的 $p_i$ 的 $\theta$ 次方占所有模型对应值的 $\theta$ 次方和,也是在算占比,只是进行了缩放。
$$
w_i = \frac{p^{\theta}i}{\sum^{K}{k=1}p^{\theta}{k}}, \theta \in \mathbb{N}
$$
当然以上这个计算公式(3)只是适用于低精度模型的权重计算中的loss计算,对于高精度模型的权重计算是这样的。首先是进行留一法交叉验证,也就是对于全精度的配置验证结果对集合 $D_K$ ,每次拿掉其中的一个 $(\mathcal{x}i, y_i)$ 训练一个去除该点的代理模型 $M{K}^{-j}$,而总共会有 $N_K$ 个这样的代理模型。计算公式:
$$
\mathcal{L^{‘}}(M_K) = \sum^{N_K}_{j=1}\sum _{k=1}^{N_K} \mathbb{1} ((\mu_K^{-j}(\mathcal{x_j}) < \mu_K^{-j}(\mathcal{x_k})) \oplus (y_j < y_k))
$$
这里 $-j$ 代表拿掉 $(x_j, y_j)$,在每个代理模型 $M_K^{-j}$ 上统计配置的验证结果和真实结果(高精度结果)不一致数量,当 $\vert D_K \vert$ 大于5之后统一都只有五折交叉验证。举个例子:
假设 $D_K = {(x_1, y_1), (x_2, y_2), (x_3, y_3), (x_4, y_4), (x_5, y_5) }$,那么我们先拿掉 $(x_1, y_1)$ 用剩下的数据训练得到 $M_K^{-1}$,验证的时候比较 $y_1$ 和其它配置的性能 $y_i$ 的大小关系并统计和真实值(高精度结果)不一致的数量。对每个模型都重复这样的过程。
还有值得注意的时候,如果一开始高精度验证结果的数量小于3,则对于低精度权重统一设置为 $w_i = \frac{1}{K - 1}$,高精度的权重为0,这是因为此时低精度的拟合比高精度的拟合更可信。
算法的伪代码如下:


FlexHB
对MFES-HB做了改进。
FGF
首先是作者认为说不同精度的数据分布不够平坦,低精度的数据很多而高精度的验证数据比之相比特别少;并且在早期能够用来拟合模型的数据很少并且数据的增加也很慢;还有就是使用的精度不够多,并且精度之间的过渡过于陡峭,基础模型的个数比较少。
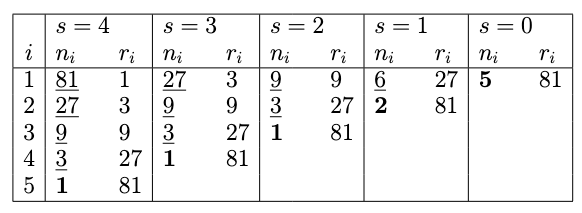
所以作者做的第一个改进是增加了每个bracket内部sh过程中评估配置的精度组,从原来的按照 $\eta$ 进行指数增加变成了每间隔 $\eta$ 一组,与普通sh相比增加出来多评估的精度组中配置的数量与本bracket内最高精度组也就是 $r_i = R$ 时配置的数量相同。如下所示。
有了这样的改进后每个低精度基础模型的权重计算方法和MFES-HB保持一致,但作者改进了MFES-HB高精度模型使用交叉验证计算权重的方法,后面有实验表明这种做法计算出来的权重 $w_K$ 比其它基础模型的权重 $w_i$ 小很多。由于经FGF改进之后的fidelity的数值大小是线性增长的,并且现在前一个精度验证的配置个数和最后一个是一样的,即 $\vert D_k \vert = \vert D_{K-1} \vert$,所以我们可以用前一个的精度的loss的结果进行缩放。现在的做法是对 $D_{K-1}$ 和 $D_K$ 都计算交叉验证的 ranking loss,如公式(6),分别得到 $L_{K-1}^{‘}$ 和 $L_{K}^{‘}$ ,然后根据如下公式计算 $p_{K}$:
$$
p_K = p_{K-1} · \frac{L_K^{‘}}{L_{K-1}^{‘}}
$$
GloSH
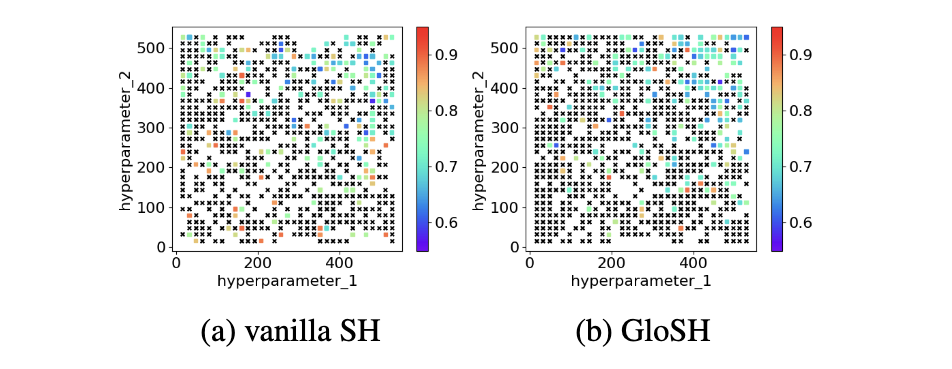
其次是作者认为呢一个配置在低精度场景下性能一般不能代表说它在高精度场景表现就一定不好(?那是否可以说sh这个算法其实是不完备的)下面这个图是在所有精度下都验证了所有的配置,越蓝是越好的配置,最后一张子图里面打叉的是在低精度场景表现不好而被提前终止的配置,可以看到在精度为27的情况下很多表现比较好呈现蓝色的点对应到最后一张子图都被打叉即提前终止了。
所以作者的第二个想法是能不能设置一个复活机制,让前面bracket被抛弃的配置能在后面复活且被再次进行验证,也就是说对于相同精度验证下的资源应该进行全局排序而不是在bracket内部进行排序,这样这个原来被抛弃的配置很有可能在其它bracket被进行进一步在更多精度下进行验证。
这部分的实现通过维护一个集合 $S = { S_0, \dots, S_m }$ 来实现,这个集合包含了原先其它bracket中所有在精度 $r_i$ 下早停的配置,是否重启一个配置 $S_i$ 使用参数 $\lambda_i$ 来控制,当 $\lambda_i = 0$ 的时候GloSH其实就退化成了普通的 sh。

FlexBand
最后是作者认为对每个bracket使用固定的 $n_i$ 和 $r_i$ 是不合理的,他认为应该一个优秀的算法应该是能进行自适应调整的,他的改进策略是衡量相同的配置在两个bracket初始精度下的 metric ranking of configuration的相似度,也就是说如果一组相同的配置在两个bracket初始情况下的排名是一致的,其实没必要再浪费资源跑两个bracket(If rankings at two fidelity levels are similar, we can expect the capability for fulfilling the potential of a candidate of these two levels are almost same)
具体来说呢,给定一组在精度 $r_i$ 下已经验证过的结果 $D_i = { (X_{i,1}, y_{i,1}), \dots, (X_{i,n}, y_{i,n})}$ ,在上一个更低精度下 $r_{i-1}$ 验证的结果 $D_{i-1}$ 中找到它们对应的结果,即 $D_{i; i-1} = { (X_{i}, y_{i-1}) \in D_{i-1} \vert X_i \in D_i}$。然后计算这两个集合的相似关系,这里用到了Kendall-tau系数,其范围在-1到1之间,通常用于评价预测排序和真实排序的相关性。如果为1则代表完全正相关,为-1为完全负相关,为0则代表无关联。这里的concordant和disconcordant分别是在两个相邻精度下预测结果排序的一致和不一致,通常这个 $\tau$ 设置为0.55。
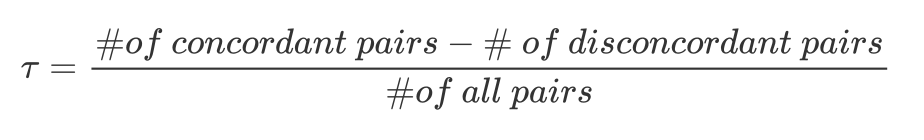
FlexBand的算法伪代码如下所示。

这里的 $D$ 应该是预先根据bohb每个bracket的初始化方法都只跑了每个bracket的第一轮的结果,根据这个结果去从最exploitation的bracket开始计算两两间隔精度结果的相似性从而分配每个bracket初始化对应的 $n$ 和 $r$。所有分配完成后就正常开始在每个bracket执行sh或者前面说的glosh。下面这张图是一个示例。
experiment
settings
- baselines
- random search
- smac
- batch-bo (a parallelized BO method that concurrently evaluating candidates)
- hyperband
- bohb
- mfes
- tse (a multi-fidelity BO method samples smaller subsets of training data and utilizes their low fidelity measurements)
- boms (BO with Median Stop, a candidate is stopped if its best metric at some step is worse than a median value calculated based on history configurations)
- bocf (BO using Curve Fitting method to predict fullfidelity metric for early stopping determination)
- tuning task
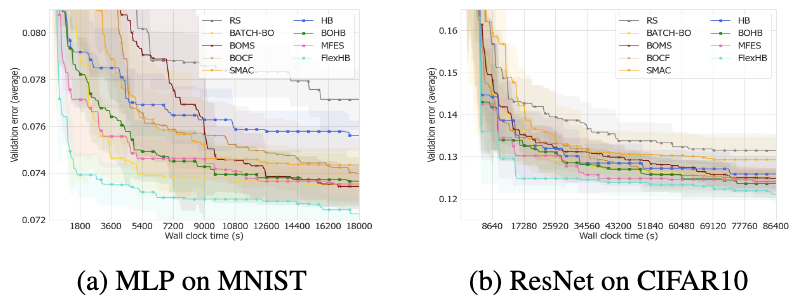
- MLP: Tuning a 2-layer MLP on MNIST.
- ResNet: Tuning ResNet on CIFAR-10.
- LSTM: Tuning a 2-layer LSTM on Penn Treebank
- Traditional ML model: Tuning XGBoost on several classification datasets: Covertype, Adult, Pokerhand and Bank Marketing
- LCBench: a public HPO benchmark, containing learning curve data for 35 OpenML datasets.
results
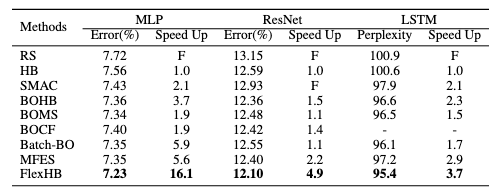
- hpo performance
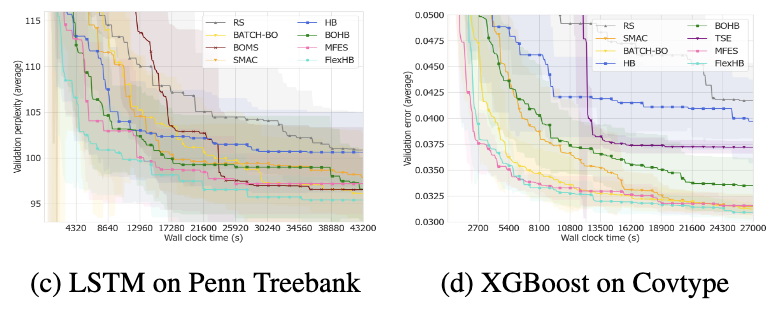
analysis of fgf weights
在MFES中,最低和最高精度的权重远小于中间精度模型的权重。当r = 27时,权重值没有显著增加,直觉来看这是非常不合理的(因为这部分的策略应该可以更好地估计f)。在FlexHB中,最低精度的权重随着调优的进行而减小,同时,高精度模型的权重在不断增加。而且随着更多高精度测量值的收集,高精度和中等精度模型的权重的差异逐渐增大。这样的结果显然是更合理的。
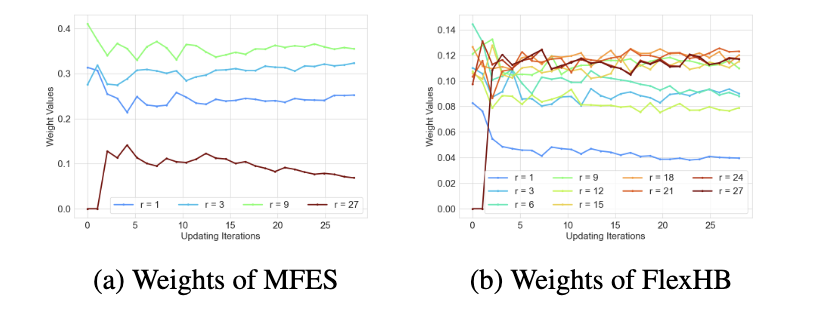
analysis of glosh
复活后的一些配置最终有取得较好结果的(蓝色点)
analysis of sh arrangements
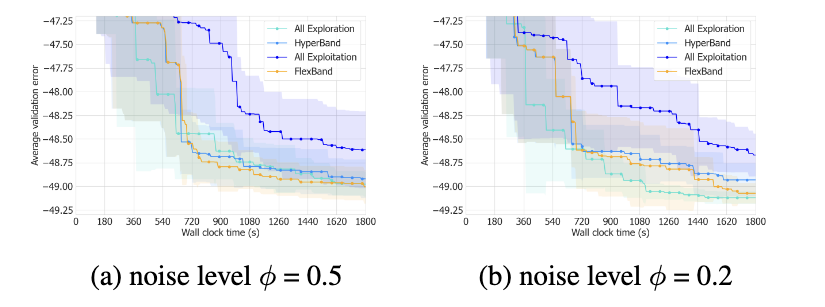
造了一个数据集并且用参数 $\phi$ 来控制生成的配置的方差,$\phi$ 值越大的话生成的配置的方就差越大,这种不稳定性对于小精度来说是很难区分的。
从下图中我们可以看到在左图中hyperband和all exploration(也就在所有bracket里面初始化精度都为 $r_0 = 1$ )方法的效率是相似的,但在总体方差更小的配置上all exploration效率是更高的且收敛结果更好。
所以虽然说相比于all exploitation(也就是所有bracket里面初始化精度都为 $r_0 = R$)hyperband可以通过低精度尝试和探索更多更优秀的配置并且取得更好的效果,但在配置反差较大的时候他取得的性能确实一般,在反差较小的时候还不如直接从最低精度开始搜索的效率高。
从实验结果看FlexHB这种self-adaptive的方法确实可以更好balance各种情况。
ablation study
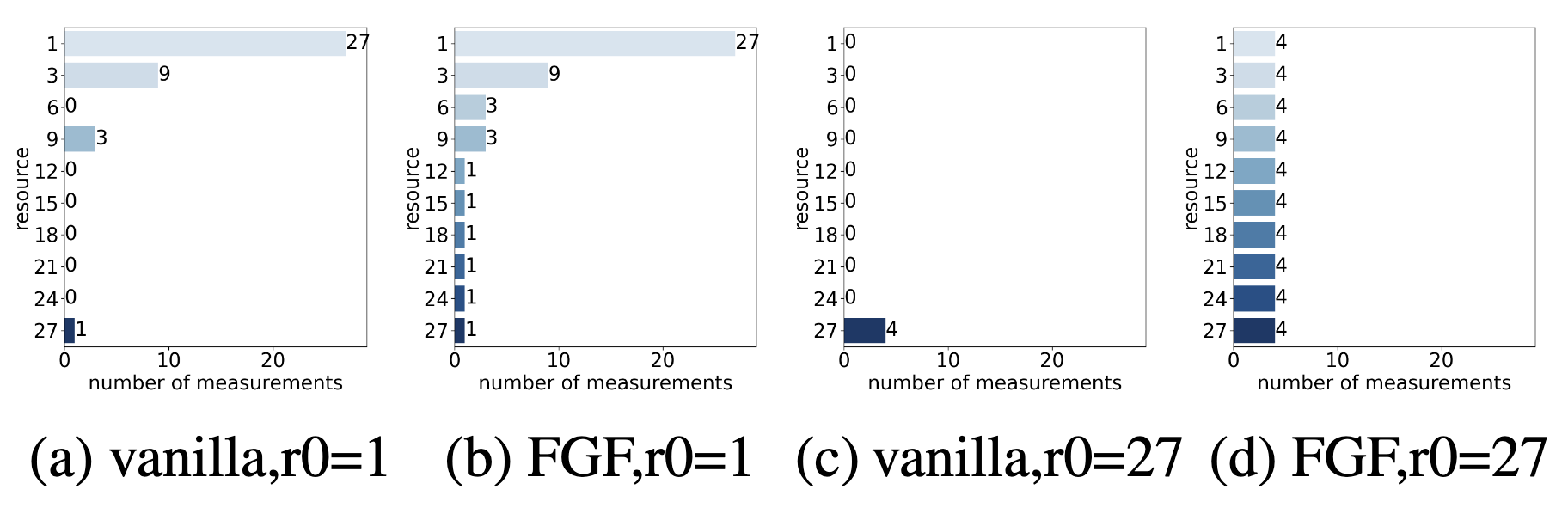
这里的improve是相对于hyperband的,$\Delta$ 是相对于FlexHB。