TUNIVERSE

TUNIVERSE

knobs调优实验

knobs调优实验

database

字数统计: 5.8k阅读时长: 22 min

 2024/09/21  4  Share

• 
  
• 
• 
• 
• 

evaluation

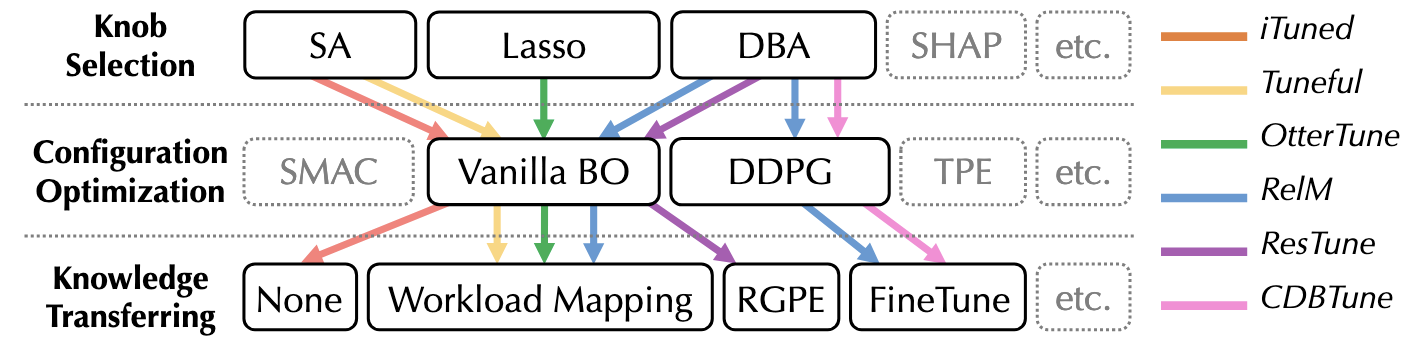
methodology

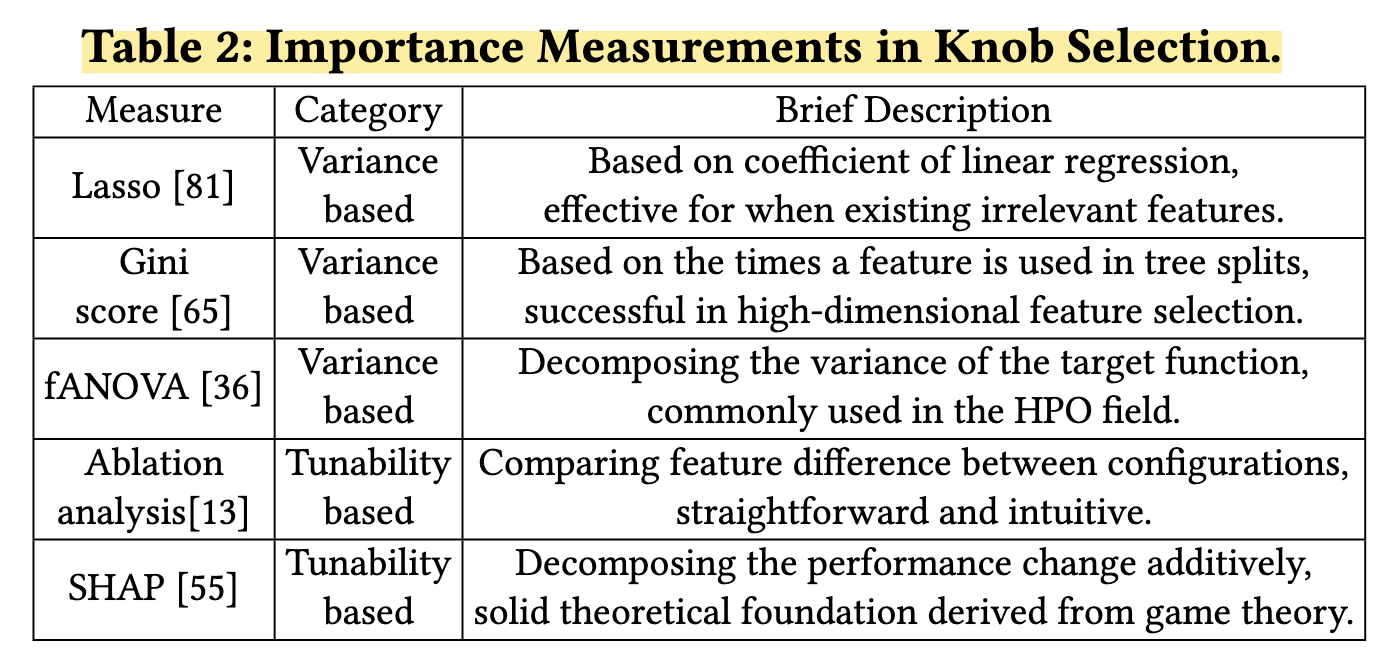
knob selection

第一种variance-based的方法选择对数据库性能影响最大的旋钮（衡量knob的重要性）；

第二种tunability-based的方法通过量化旋钮的可调谐性，衡量从其默认值到另一个值变化所能获得的性能增益。

variance-based

• Lasso：使用线性回归系数来评估旋钮的重要性。它对系数的L1范数进行惩罚，并使冗余knob的系数为零，可以有效过滤无用的knob。但它粗暴地做了线性关系的假设，无法捕捉knob与performance之间的非线性关系。
• Gini系数：定义每个knob的Gini系数为给定的knob在所有决策树的分裂中作为candidate属性的次数（因为作者认为重要的knob区分了更多的样本，并且在树的分割中会使用的更频繁）
• faNOVA：Functional analysis of variance。通过分析每个knob在整个配置空间中对目标函数方差的贡献程度来衡量knob的重要性。基于回归模型，faNOVA将目标函数分解成仅依赖于其输入子集的加性成分，每个knob的重要性通过其方差分数来量化。

tunability-based

• ablation analysis：选择变化贡献最大的knob来提高配置的性能。
• SHAP：计算每个knob的贡献（即SHAP值）。在一个最大化问题中，给定一组observation，其通过平均每个knob的SHAP正值来计算每个knob的tunability。

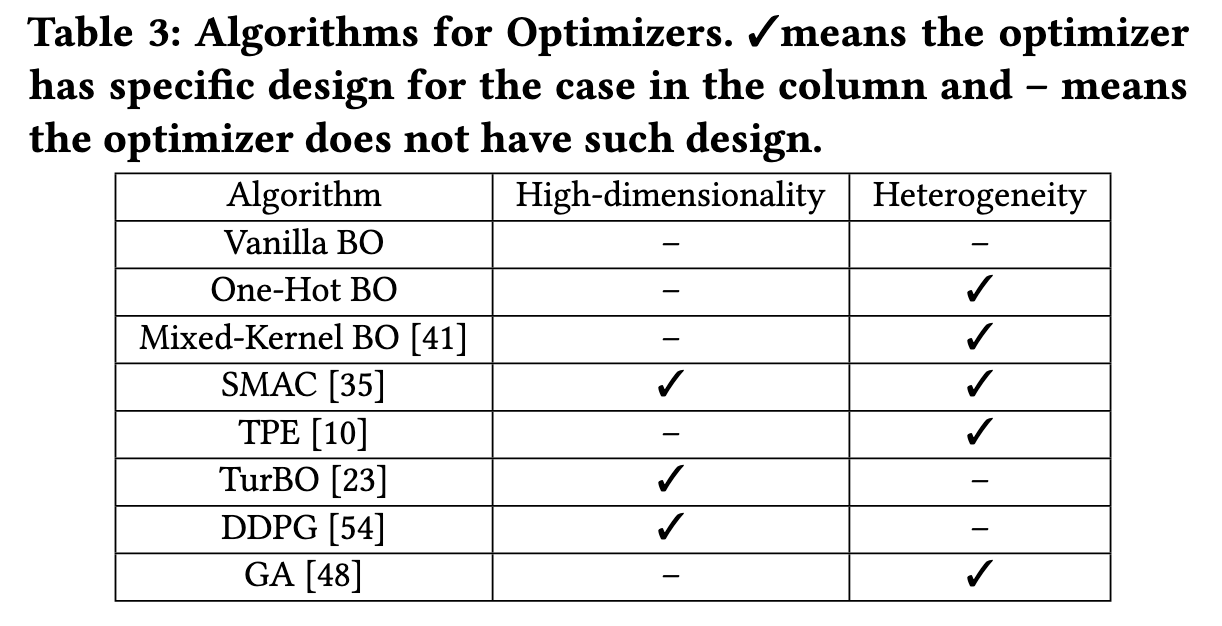
configuration optimization

• Vanilla bo：以gp为代理模型的贝叶斯优化模型，使用核函数来对目标函数的总体平滑程度进行建模，而vanilla bo的核函数则是基于两个配置configuration之间的欧式距离
• one-hot bo：gp代理模型局限于连续型变量的搜索优化，而这种方法选择了对离散的变量采用one-hot编码从而将具有k个可能值的变量转化为二进制向量
• mixed-kernel bo：对连续型变量使用matern kernel，对离散型变量使用hamming kernel
• smac
• tpe
• Tu RBO：trust-region bo. 它提出了一种使用independent surrogate model的方法，这些surrogate model能够对目标函数进行建模并且不回造成over-exploration
• DDPG：Deep Deterministic Policy Gradient (DDPG) algorithm. 由两个神经网络组成
• GA

knowledge transfer

pass

intra-algorithms

ablation analysis

消融分析（Ablation Analysis）是一种用于确定不同特征（参数）对系统性能影响的重要性的方法。以下是对给定段落的解释和一个具体例子：

解释

1. 初始配置和目标配置：

   • **默认配置 ${\theta }_{\text{default}}$**：系统的默认设置。
   • **目标配置 ${\theta }_{\text{target}}$**：通常是性能更好的配置。

2. **计算特征差异 $\mathrm{\Delta }({\theta }_{\text{default}},{\theta }_{\text{target}})$**：

   • 计算默认配置和目标配置之间的参数差异。

3. 构建消融路径：

   • 从默认配置 ${\theta }_{\text{default}}$ 开始，逐步改变参数，直到达到目标配置 ${\theta }_{\text{target}}$。
   • 在每次迭代 $i$ 中，从前一次的配置 ${\theta }_{i-1}$ 开始，考虑所有剩余的特征变化 $\delta \in \mathrm{\Delta }({\theta }_{\text{default}},{\theta }_{\text{target}})$。
   • 将每个特征变化 $\delta$ 应用于前一次的配置 ${\theta }_{i-1}$，得到候选配置 ${\theta }_{i-1}[\delta ]$。
   • 选择性能最好的候选配置作为下一次迭代的配置 ${\theta }_i$。
   • 性能评估通过代理模型（surrogate）进行，以提高效率。

4. 特征重要性排序：

   • 特征改变的顺序即为消融分析中的重要性排序。
   • 对于一个观察集中的多个目标配置，进行多次消融分析。
   • 每个特征的最终重要性排序是其在每条消融路径中的平均排名。

例子

假设我们有一个系统，默认配置 ${\theta }_{\text{default}}$ 和目标配置 ${\theta }_{\text{target}}$ 如下：

• **默认配置 ${\theta }_{\text{default}}$**：$A=1,B=2,C=3$
• **目标配置 ${\theta }_{\text{target}}$**：$A=2,B=3,C=5$

特征差异 $\mathrm{\Delta }({\theta }_{\text{default}},{\theta }_{\text{target}})$ 是：

• $A$ 从 1 变为 2
• $B$ 从 2 变为 3
• $C$ 从 3 变为 5

消融路径构建：

1. 初始配置：${\theta }_0={\theta }_{\text{default}}=A=1,B=2,C=3$

2. 第一次迭代：

   • 候选配置：
     • ${\theta }_0[A]=A=2,B=2,C=3$
     • ${\theta }_0[B]=A=1,B=3,C=3$
     • ${\theta }_0[C]=A=1,B=2,C=5$
   • 选择性能最好的候选配置（假设是 ${\theta }_0[C]$），所以 ${\theta }_1=A=1,B=2,C=5$

3. 第二次迭代：

   • 候选配置：
     • ${\theta }_1[A]=A=2,B=2,C=5$
     • ${\theta }_1[B]=A=1,B=3,C=5$
   • 选择性能最好的候选配置（假设是 ${\theta }_1[A]$），所以 ${\theta }_2=A=2,B=2,C=5$

4. 第三次迭代：

   • 剩下的唯一候选配置：
     • ${\theta }_2[B]=A=2,B=3,C=5$
   • 所以 ${\theta }_3=A=2,B=3,C=5$ 即 ${\theta }_{\text{target}}$

特征重要性排序：

• 第一次改变的是 $C$，所以 $C$ 的重要性最高。
• 第二次改变的是 $A$，所以 $A$ 的重要性次之。
• 最后改变的是 $B$，所以 $B$ 的重要性最低。

SHAP

SHapley Additive exPlanations 是一种基于博弈论的解释方法，用于解释机器学习模型的预测。它通过计算每个特征对预测结果的贡献来解释模型的输出。SHAP值是基于Shapley值的，这是一种源自合作博弈论的分配方法，用于公平地分配合作收益。

解释

1. SHAP值的定义：

   • SHAP值使用原始模型的条件期望函数的Shapley值来解释每个特征对模型预测的贡献
   • 每个特征的SHAP值表示在考虑该特征时，期望模型预测的变化

2. 基值和当前输出：

   • 基值（base value）是指在不了解任何特征时模型的预测值。
   • 当前输出是指在给定所有特征时模型的预测值

3. 特征添加顺序的重要性：

   • 当模型是非线性的或输入特征不是独立的，特征添加到期望值中的顺序会影响SHAP值。
   • SHAP值通过对所有可能的特征添加顺序进行平均来计算

4. SHAP值的计算：

   • 通过Shapley采样值方法或Kernel SHAP方法来估计SHAP值
   • 精确计算会比较困难

例子

使用机器学习模型来预测不同配置下的数据库性能，并希望解释每个配置参数对性能的影响。

示例配置参数

• **innodb_buffer_pool_size**：InnoDB缓冲池大小
• **max_connections**：最大连接数
• **query_cache_size**：查询缓存大小

假设有以下两个配置：

• **默认配置 ${\theta }_{\text{default}}$**：

  • innodb_buffer_pool_size = 1GB
  • max_connections = 100
  • query_cache_size = 64MB

• **目标配置 ${\theta }_{\text{target}}$**：

  • innodb_buffer_pool_size = 4GB
  • max_connections = 200
  • query_cache_size = 128MB

使用SHAP值解释配置对性能的影响

1. 基值和当前输出：

   • 基值：如果我们不知道任何配置参数，模型预测的性能基值（例如每秒查询数QPS）是 1000 QPS
   • 当前输出：给定目标配置，模型预测的性能是 1400 QPS

2. 计算SHAP值：

   • **innodb_buffer_pool_size**：
     • 如果只考虑 innodb_buffer_pool_size，从1GB增加到4GB，模型预测的性能是 1150 QPS
     • 因此，innodb_buffer_pool_size 的 SHAP 值是 $1150-1000=150$ QPS
   • **max_connections**：
     • 如果只考虑 max_connections，从100增加到200，模型预测的性能是 1250 QPS
     • 因此，max_connections 的 SHAP 值是 $1250-1000=250$ QPS
   • **query_cache_size**：
     • 如果只考虑 query_cache_size，从64MB增加到128MB，模型预测的性能是 1100 QPS
     • 因此，query_cache_size 的 SHAP 值是 $1100-1000=100$ QPS

3. 特征的顺序：

   • 由于数据库性能模型可能是非线性的，配置参数的顺序会影响SHAP值的计算
   • SHAP值通过对所有可能的配置参数顺序进行平均来计算

4. 总贡献：

   • innodb_buffer_pool_size 的 SHAP 值：$150$ QPS
   • max_connections 的 SHAP 值：$250$ QPS
   • query_cache_size 的 SHAP 值：$100$ QPS
   • 总贡献：$150+250+100=500$ QPS
   • 加上基值 $1000$ QPS，总预测值是 $1500$ QPS（与模型预测的 $1400$ QPS 接近，可能有一些近似误差）

SMAC

解释

1. 构建随机森林模型：

   • 收集一些初始数据点（例如，不同配置下的性能数据）
   • 使用这些数据点构建随机森林，每棵树是在从整个数据集中随机抽样得到的n个数据点上构建的
   • 随着更多配置被评估，模型会不断更新，以包含新的数据点

2. 预测均值和方差：

   • 对于每个候选配置 $\theta$，模型会生成一个预测分布，同时计算其预测均值 $\hat{\mu }(\theta )$ 和方差 ${\hat{\sigma }}^2(\theta )$。

3. 计算期望正改进（EI）：

   • 使用前面生成的预测分布计算每个候选配置 $\theta$ 的EI值，$\text{EI}(\theta )$，它能够考虑预测性能和预测不确定性；

   • EI值的计算公式如下：

     $$\text{EI}(\theta )=\mathbb{E}[max(0,f(\theta )-f({\theta }_{\text{best}}))]$$

     其中，$f(\theta )$ 是配置 $\theta$ 的预测性能，$f({\theta }_{\text{best}})$ 是目前最佳配置的性能；

   • 例如，假设目前最佳配置的性能是 2000 QPS。如果新配置 $\theta$ 的预测均值是 2100 QPS，预测方差是 100 QPS，那么 $\theta$ 的EI值会较高，因为它既有较高的预测性能，又有一定的不确定性。

4. 多起点局部搜索：

   • 从多个初始配置开始，每个初始配置都进行局部优化以找到局部最大EI的配置。
   • 例如，从默认配置 ${\theta }_{\text{default}}$ 开始，逐步调整 innodb_buffer_pool_size，max_connections，和 query_cache_size，寻找使EI值最大的配置。

5. 选择最优配置：

   • 选择具有最高EI值的配置作为下一个评估的配置，实际评估该配置的性能，并将结果添加到数据集中，更新随机森林模型
   • 例如，假设找到的最优配置是 innodb_buffer_pool_size = 2GB，max_connections = 150，query_cache_size = 128MB，并且在实际评估中，它的性能提升到 2200 QPS。

例子

示例配置参数

• **innodb_buffer_pool_size**：InnoDB缓冲池大小
• **max_connections**：最大连接数
• **query_cache_size**：查询缓存大小

假设有以下默认配置：

• **默认配置 ${\theta }_{\text{default}}$**：
  • innodb_buffer_pool_size = 1GB
  • max_connections = 100
  • query_cache_size = 64MB

目标是找到一个比默认配置更好的配置，以提高数据库的性能（例如每秒查询数QPS）

使用SMAC进行调优

初始性能测量结果：${\theta }_{\text{default}}$ 的性能是 1000 QPS

随机生成一些初始配置并测量它们的性能：

• 配置A：innodb_buffer_pool_size = 2GB, max_connections = 100, query_cache_size = 64MB，性能是 1100 QPS；

• 配置B：innodb_buffer_pool_size = 1GB, max_connections = 200, query_cache_size = 64MB，性能是 1050 QPS；

  ……

• 配置E：innodb_buffer_pool_size = 1GB, max_connections = 100, query_cache_size = 128MB，性能是 1020 QPS；

使用这些初始数据，SMAC构建了一个随机森林模型，并计算了每个候选配置的预测均值和方差

下一步，SMAC计算每个候选配置的EI值，选择EI值最高的配置进行评估。例如：

• 配置D：innodb_buffer_pool_size = 2GB, max_connections = 150, query_cache_size = 128MB，预测均值是 1200 QPS，预测方差是 50 QPS，EI值最高

实际评估配置D的性能，结果是 1150 QPS，将这个结果添加到数据集中，并更新随机森林模型

通过多次迭代，SMAC逐步探索和优化配置参数，最终找到一个最佳配置

RGPE

RGPE（Ranked Gaussian Process Ensemble）是一种可扩展的元学习框架，用于加速基于贝叶斯优化的优化器

解释

1. 基本过程：

   • 对于每个先前的调优任务 $T_i$，RGPE都在相应的观察数据 $H_i$ 上训练一个基本高斯过程（GP）模型 $M_i$
   • 然后，它构建一个代理模型 $M_{\text{meta}}$，结合这些基本GP模型，而不是仅仅使用拟合在目标任务 $H_T$ 上的原始代理模型 $M_T$。

2. 预测：

   • 在点 $\theta$ 处，$M_{\text{meta}}$ 的预测由以下公式给出：
     $$y\sim N(\sum _i{w}_i{\mu }_i(\theta ),\sum _i{w}_i{\sigma }_i^2(\theta ))$$
   • 其中，$w_i$ 是基本代理 $M_i$ 的权重，${\mu }_i$ 和 ${\sigma }_i^2$ 分别是基本代理 $M_i$ 的预测均值和方差。
   • $w_i$ 反映了先前任务与当前任务之间的相似性。

3. 相似性度量：

   • $M_{\text{meta}}$ 利用先前调优任务的知识，可以大大加速目标任务的收敛。
   • 使用以下排名损失函数 $L$ 来度量先前任务与目标任务之间的相似性：
     $$L(M_j,H_T)=\sum _{j=1}^{n_t}\sum _{k=1}^{n_t}\mathbb{1}((M_i({\theta }_j)\le M_i({\theta }_k))\oplus (y_j\le y_k))$$
   • 其中，$n_t$ 表示调优任务的数量，$M_i({\theta }_j)$ 表示 $M_i$ 在配置 ${\theta }_j$ 上的预测值。

4. 权重计算：

   • 基于排名损失函数，权重 $w_i$ 设置为 $M_i$ 在 $H_T$ 上具有最小排名损失的概率：
     $$w_i=\mathbb{P}(i=\arg \underset{j}{min}L(M_j,H_T))$$
   • 这个概率可以通过MCMC采样估计

例子

示例配置参数（Knobs）

• **innodb_buffer_pool_size**：InnoDB缓冲池大小
• **max_connections**：最大连接数
• **query_cache_size**：查询缓存大小

假设我们有以下默认配置：

• **默认配置 ${\theta }_{\text{default}}$**：
  • innodb_buffer_pool_size = 1GB
  • max_connections = 100
  • query_cache_size = 64MB

使用RGPE进行调优

1. 训练基本GP模型：

   • 对于每个先前的调优任务，我们在相应的观察数据上训练一个基本GP模型 $M_i$。

2. **构建代理模型 $M_{\text{meta}}$**：

   • 结合这些基本GP模型，构建 $M_{\text{meta}}$，而不是仅仅使用拟合在目标任务上的原始代理模型。

3. 预测均值和方差：

   • 对于新配置 $\theta$，计算其预测均值 $\sum _i{w}_i{\mu }_i(\theta )$ 和方差 $\sum _i{w}_i{\sigma }_i^2(\theta )$。

4. 计算相似性和权重：

   • 使用排名损失函数 $L$ 来度量先前任务与目标任务之间的相似性。
   • 基于排名损失函数，计算每个基本GP模型的权重 $w_i$。

5. 选择最优配置：

   • 选择具有最高预测性能的配置作为下一个评估的配置。
   • 实际评估该配置的性能，并将结果添加到数据集中，更新代理模型。

具体例子

假设我们正在优化一个MySQL数据库的配置参数，目标是最大化每秒查询数（QPS）。我们有以下配置参数：

• **innodb_buffer_pool_size**：InnoDB缓冲池大小
• **max_connections**：最大连接数
• **query_cache_size**：查询缓存大小

初始配置 ${\theta }_{\text{default}}$：

• innodb_buffer_pool_size = 1GB
• max_connections = 100
• query_cache_size = 64MB

初始性能测量结果：

• ${\theta }_{\text{default}}$ 的性能是 1000 QPS。

我们在先前的调优任务上训练了一些基本GP模型，并结合这些模型构建了 $M_{\text{meta}}$。

下一步，RGPE计算每个候选配置的预测均值和方差，并选择具有最高预测性能的配置进行评估。例如：

• 配置A：innodb_buffer_pool_size = 2GB, max_connections = 150, query_cache_size = 128MB，预测均值是 1200 QPS，预测方差是 50 QPS。

实际评估配置A的性能，结果是 1150 QPS。将这个结果添加到数据集中，并更新代理模型。

通过多次迭代，RGPE逐步探索和优化配置参数，最终找到一个最佳配置，显著提高了数据库的性能。

experiments

general setup

Q1: How to determine the tuning knobs? (i.e., Which importance measurements to use and how many knobs to tune?)

Q2: Which optimizer is the winner given different scenarios?

Q3: Can we transfer knowledge to speed up the target tuning task? We describe the general setup of the evaluation in this section and leave the specific setting (e.g., procedure, metrics) when answering the corresponding questions.

hardware

所有的默认配置都适用mysql的默认配置，除了一个knob那就是buffer pool size因为mysql默认的这个值太小了。实验中这个值最终使用的大小是内存的60%，16GB*60%。

workloads

Q1和Q2 => 分析型负载JOB和事务性负载SYSBENCH

Q3 => 使用OLTP负载，SYSBENCH/ TPC-C/ Twitter

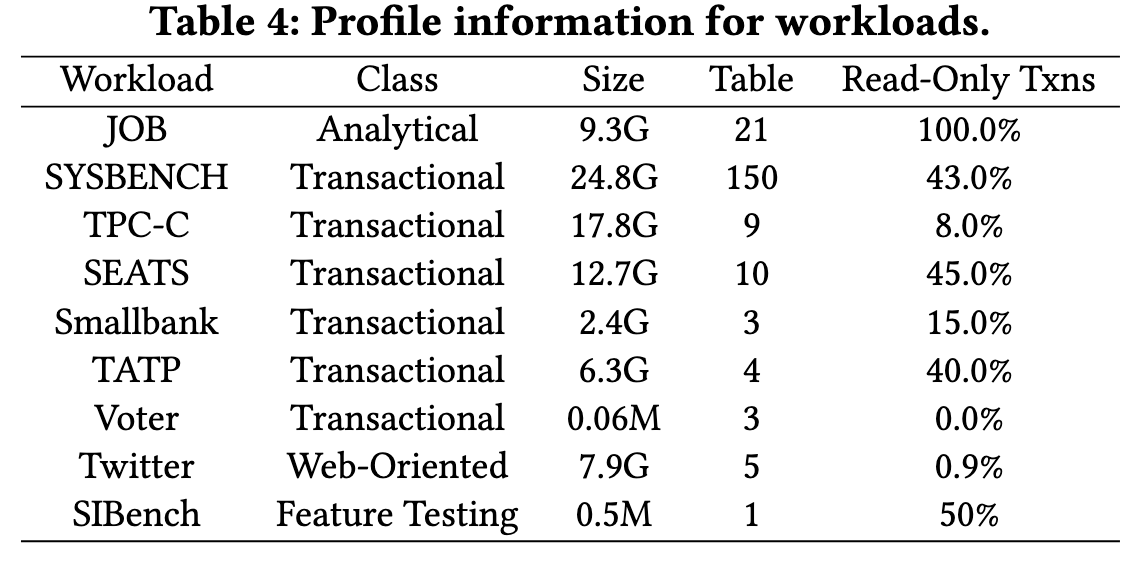
tuning setting

• mysql里一共197个knob，把实验的配置空间分为小、中、大三个大小，按照knob的重要性排序后调整的knob的数量分别是5、20、197。

• OLTP负载使用吞吐量作为最大化目标，OLAP负载使用95%分位的延迟作为最小化目标。

• 每个optimizer运行三个tuning sessions，每个session由200轮迭代组成，并且最后报告最好性能的中位数和四分位数

  • 由于很多knob的改变都需要重新启动数据库，所以实验中会进行三分钟的压力测试，回放给定的工作负载
  • 对于造成DBMS崩溃或者无法启动的负载，都将其迭代的结果设置为迭代过程中最差的performance
  • iTuned和OtterTune方法后都执行LHS采样然后生成10个配置用于BO的初始化

• 每个报告里都记录调优后相对于knob默认配置下性能的提升

knob selection

which importance measurement to use

性能排名分析

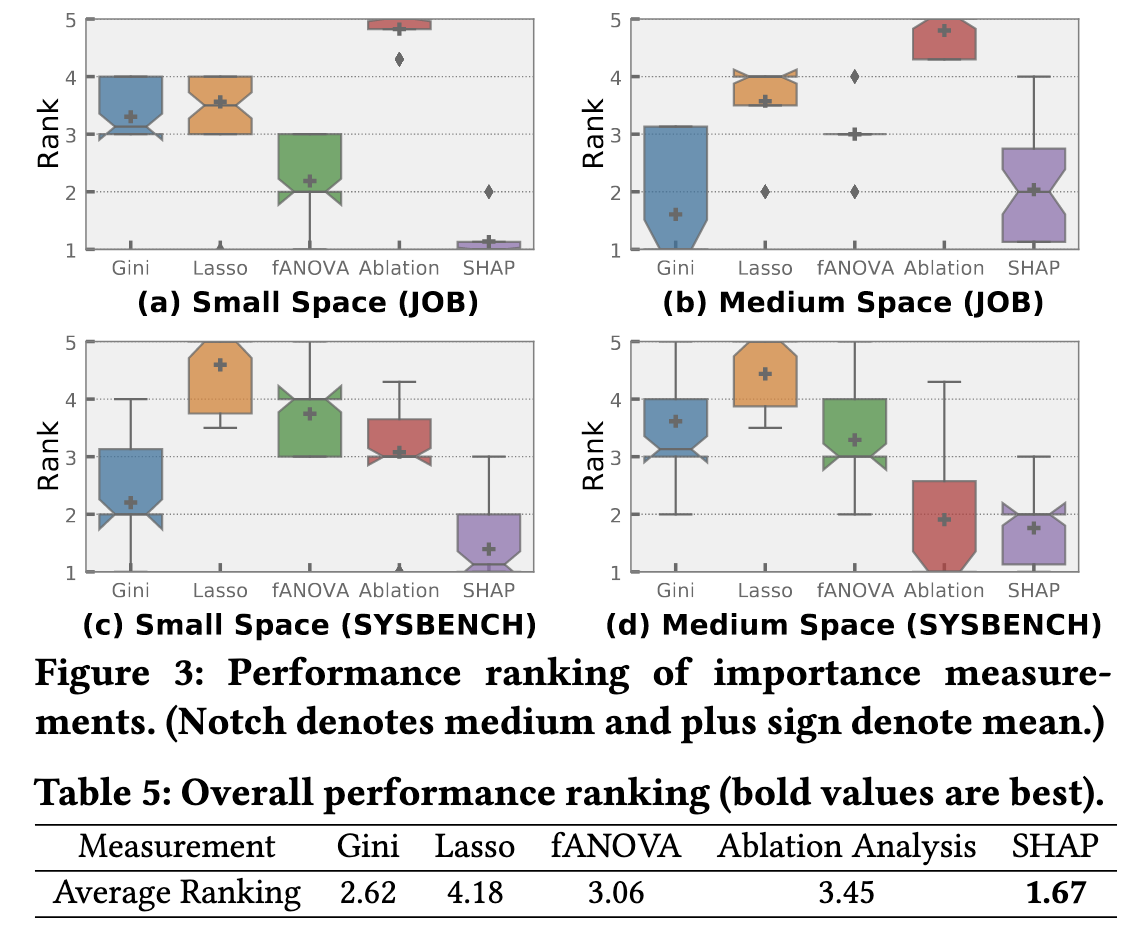
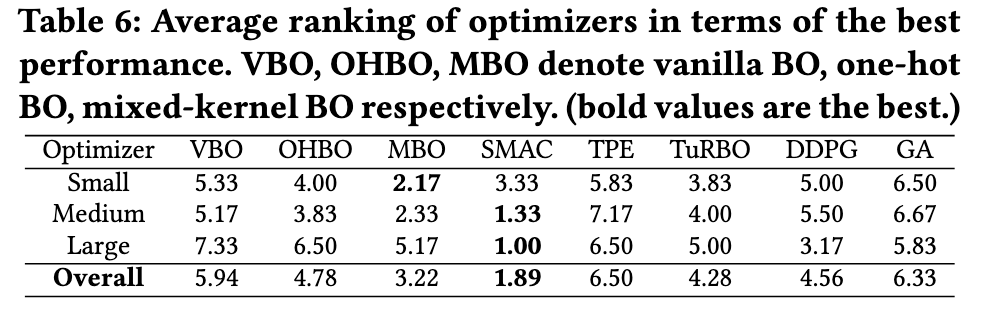
图3展示了不同重要性测量方法生成的调优集的性能排名，表5总结了这些方法的总体性能排名。

• SHAP方法在性能上表现最佳，因为它推荐值得调优的参数。当更改参数值导致数据库性能下降时，SHAP会建议不调优该参数，而基于方差的测量方法会认为该参数对性能有较大影响，需要调优。
• 数据库参数的默认值设计得较为稳健，是一个好的起点，因此基于方差的测量方法效果较差。
• 消融分析由于很大程度上依赖于高质量的训练样本，其性能不稳定，整体排名倒数第二。
• 在基于方差的测量方法中，Gini得分表现最好，而Lasso的改进效果最差，因为Lasso假设配置空间是线性或二次的，而实际存在复杂的依赖关系。

灵敏度分析

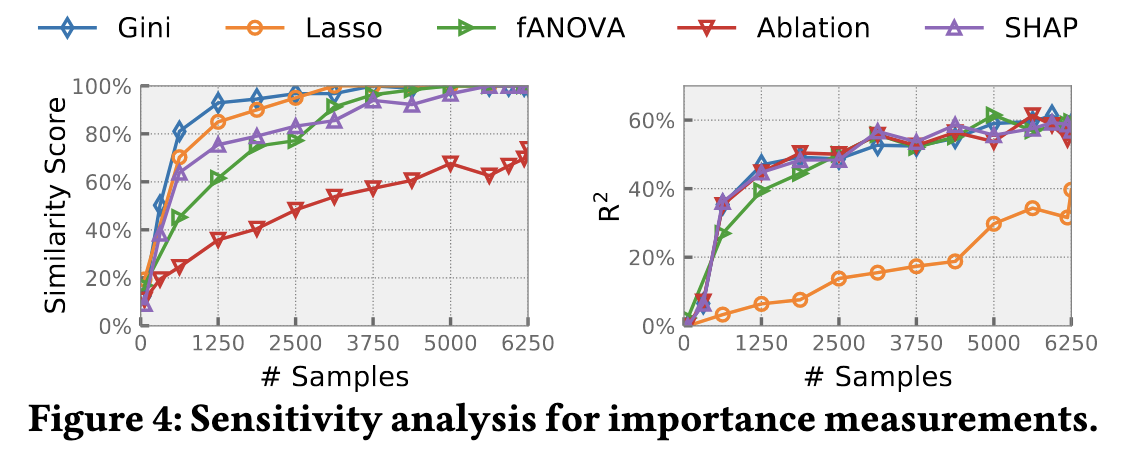
为了进一步了解不同重要性测量方法的性能差异，对SYSBENCH工作负载进行了训练样本数量的灵敏度分析，如图4所示。样本从6250个样本中随机选择，每种重要性测量方法执行10次取平均值。

左图的y轴是前5个重要参数的相似度得分（交集-并集指数），较大的相似度得分表明该测量方法更稳定，因为它能通过较少的观察找到最终的重要参数。右图绘制了验证集上的决定系数（R²），较大的R²表明代理模型能更好地建模配置与数据库性能之间的关系。

• Lasso在性能与配置之间的关系建模上效果很差，但它非常稳定。
• 消融分析的稳定性最低，因为其计算高度依赖于高质量样本。
• Gini得分的相似度最高，表明其样本效率高。
• SHAP的相似度得分与基于方差的测量方法相当，考虑到SHAP的总体性能最佳且稳定性可比，在后续研究中默认使用SHAP。

结论

• SHAP方法在性能和稳定性方面表现最佳，成为推荐的默认重要性测量方法。
• 基于方差的测量方法（如Gini）在样本效率上表现良好，但在整体性能上不如SHAP。
• 消融分析依赖于高质量样本，稳定性较差。
• Lasso假设配置空间是线性或二次的，在实际应用中效果不佳。

how many knobs to choose

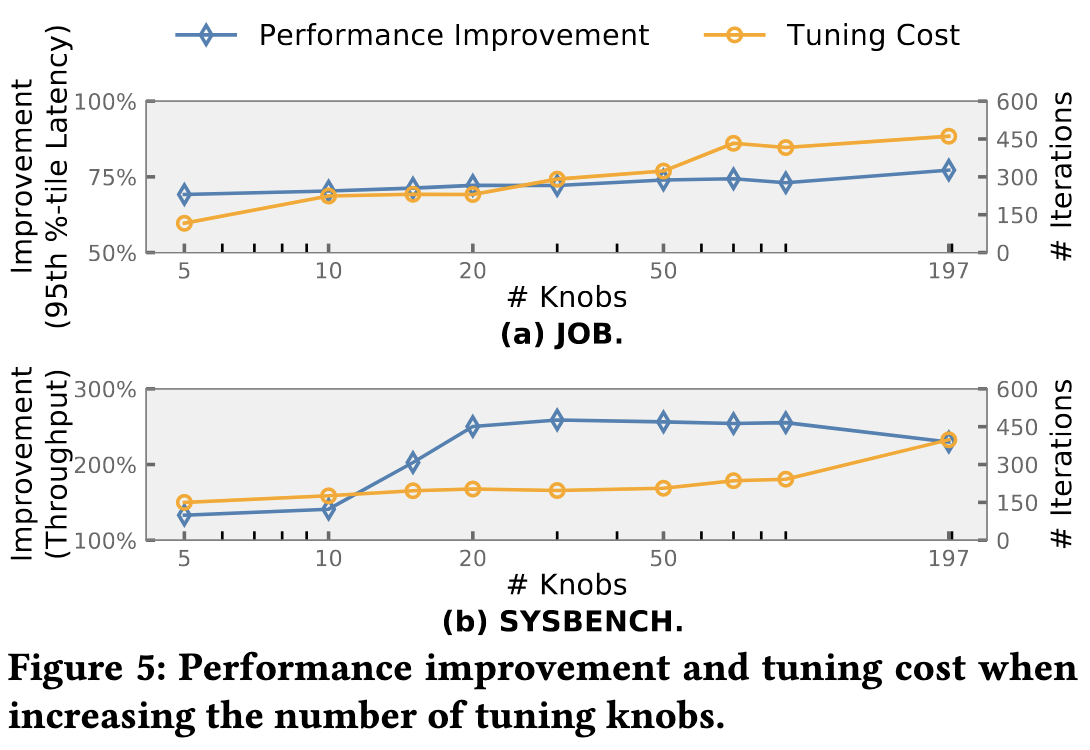
探索不同数量的knob对性能的影响:

• 首先使用SHAP对knob的重要性进行排名，然后选择不同大小的knob配置，分别观察vanilla BO在SYSBENCH和JOB上的调优性能；
• 对每个knob集合都进行600次迭代调优，记录最大性能提升和相应的调优成本（找到最大提升配置所需的迭代次数）。

实验结果

• JOB
  • 性能提升相对稳定，但调优成本随参数数量增加而增加。
• SYSBENCH
  • 初期性能提升微不足道，因为少量参数对性能影响小。
  • 随参数数量从5增加到20，性能提升从133.10%增加到250.33%。
  • 之后，性能提升因调优复杂性增加而下降。
• 结论
  • 对JOB，调优前5个参数效果最好。
  • 对SYSBENCH，调优前20个参数效果最好。
  • 在有限的调优预算下，调优参数数量应设定为适当值，小参数集影响小，大参数集调优成本高。

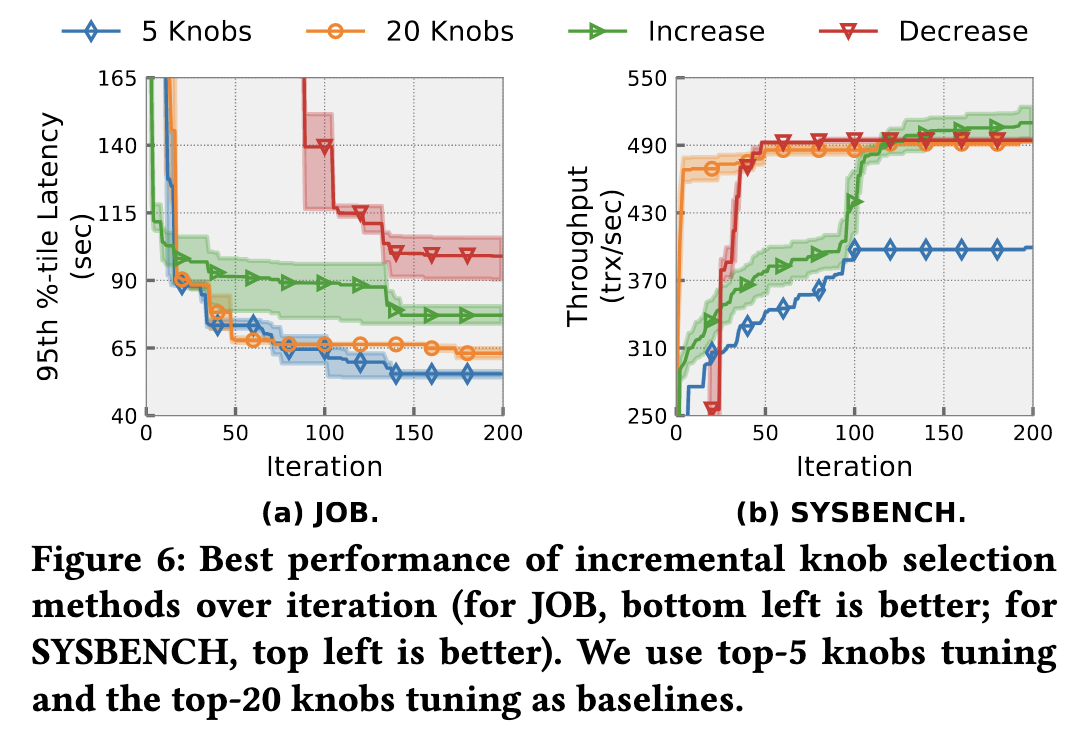
增量参数选择

• 传统方法高成本，不适用于生产环境。
• 两种增量调优启发式方法：
  1. 增加参数数量（OtterTune）：从调优前4个参数开始，每4次迭代增加2个参数。
  2. 减少参数数量（Tuneful）：从调优所有参数开始，每20次迭代移除40%的参数。
• 实验结果
  • JOB：增加或减少参数数量均不如固定调优前5个参数。
  • SYSBENCH：增加参数数量效果更好，减少参数数量限制性能提升。
• 结论
  • 对JOB，重要参数数量少，增量参数选择无额外收益。
  • 对SYSBENCH，增加参数数量方法允许优化器先探索影响最大的参数，再扩展到更大的空间。

optimizer selection

• 评估对象：八种优化器在JOB和SYSBENCH工作负载下的性能。
• 混合型配置空间验证：在JOB上构建对比实验，控制组为前20个整数参数（连续空间），测试组为前5个离散参数和前15个整数参数（混合空间）。
• 算法开销：测量推荐配置的执行时间。

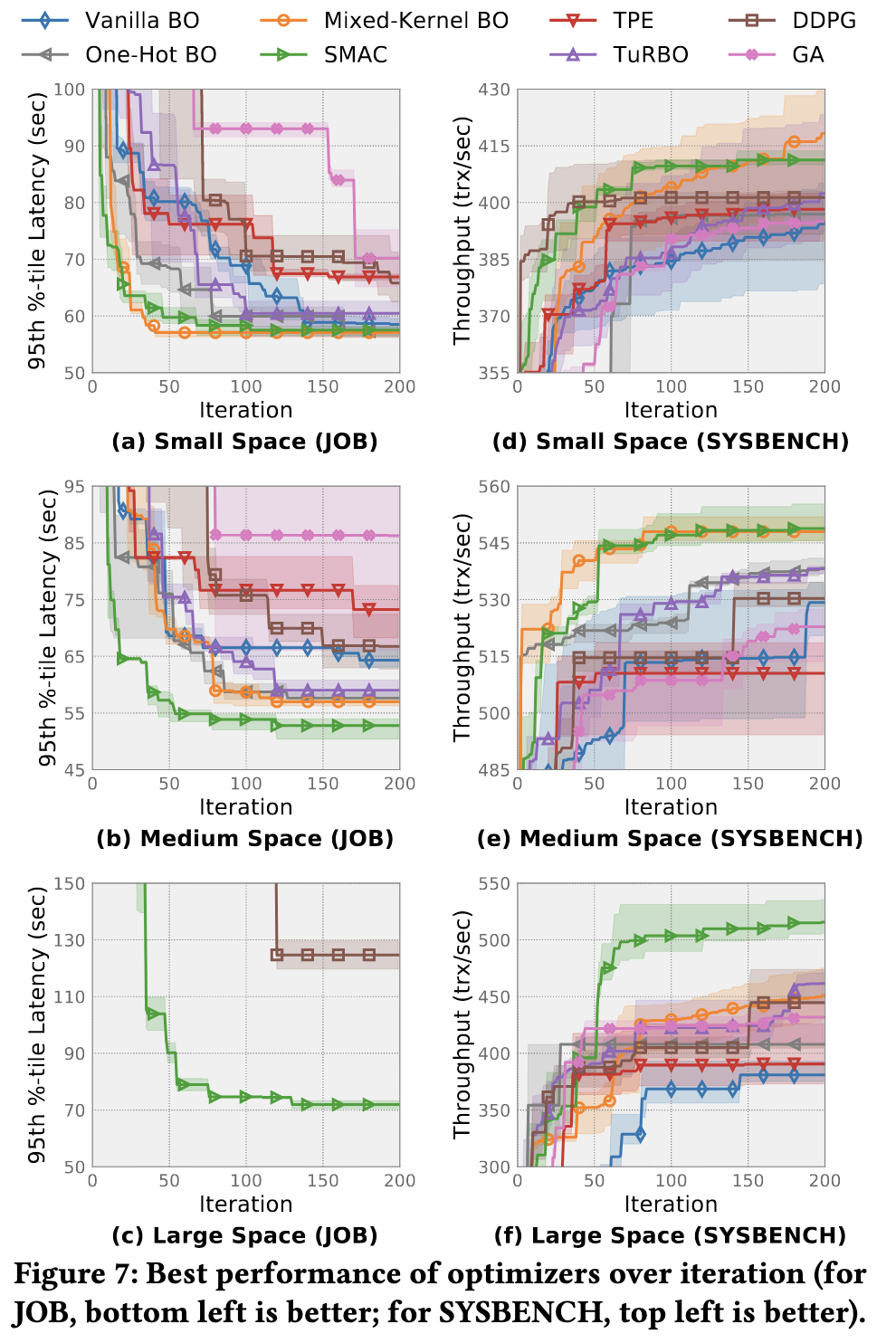
不同大小配置空间的性能

• 结果：SMAC整体性能最佳，TPE表现最差。
• 原因：SMAC采用随机森林代理，适应高维和分类输入；TPE不能建模参数间的相互作用。
• 其他优化器表现
  • GA在小和中等配置空间表现不佳。
  • SMAC和混合核BO在小和中等配置空间表现出色。
  • DDPG在小和中等空间表现差，调优成本高。
  • 大空间下，只有SMAC和DDPG找到比默认延迟更好的配置。
  • SYSBENCH大空间下，所有方法均找到改进配置，其中SMAC最佳，TuRBO次之。

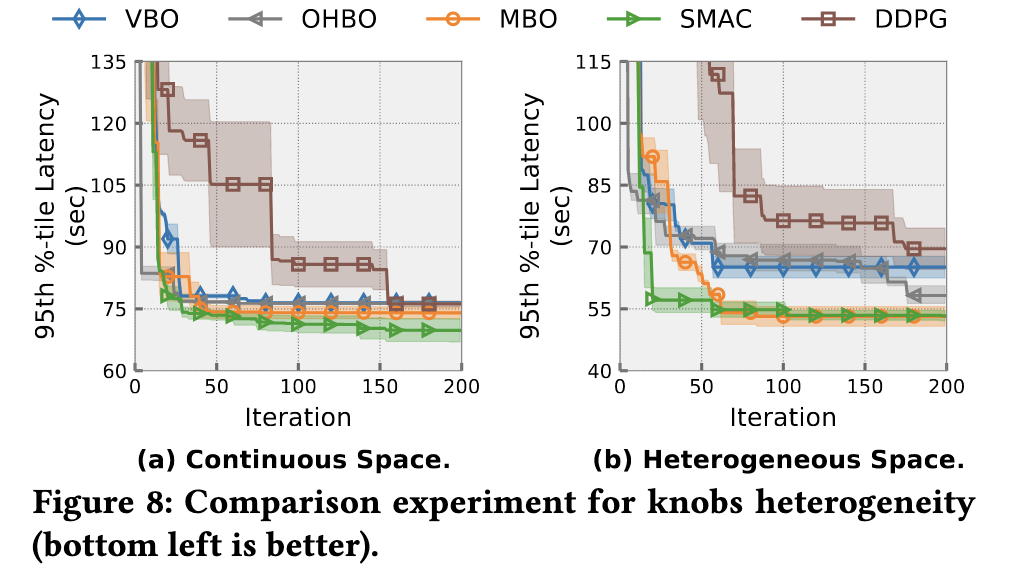
参数异构性的比较实验

• 结果：BO-based优化器在连续空间表现相似，但在异构空间表现差异较大。
• 原因
  • 混合核BO采用不同核函数处理整数和分类参数，表现最好。
  • SMAC在两种空间表现均良好。
  • DDPG调优成本高。

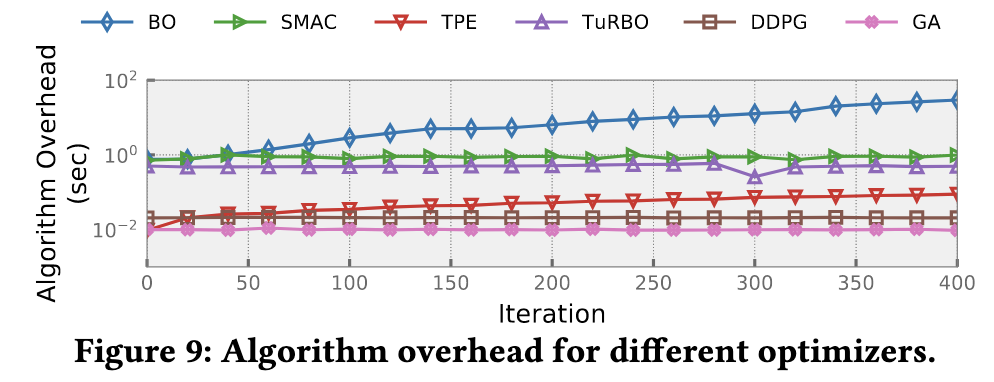
算法生成配置的开销

• 结果：BO-based优化器在连续空间表现相似，但在异构空间表现差异较大。
• 原因
  • 混合核BO采用不同核函数处理整数和分类参数，表现最好。
  • SMAC在两种空间表现均良好。
  • DDPG调优成本高。

总结

• SMAC整体性能最佳，能同时处理高维和异构配置空间，相比传统优化器（如vanilla BO, DDPG）平均性能提升21.17%。
• TPE在大多数情况下表现最差，难以建模参数间相互作用。
• DDPG在小和中等配置空间调优成本高，但在大配置空间表现较好。
• 小和中等配置空间下，SMAC和混合核BO排名前二；大配置空间下，SMAC、DDPG和TuRBO表现良好。
• 混合核BO在异构空间表现优于其他BO-based优化器。
• 全局GP-based优化器（如vanilla BO, one-hot BO和混合核BO）算法开销呈立方增长。

• Next Post
  automl-mfes-hb
• Previous Post
  knob-tuning

Powered by HexoElubrazione

PV: 6569 :)

CATALOG

1. 1. methodology
   1. 1.1. knob selection
      1. 1.1.1. variance-based
      2. 1.1.2. tunability-based
   2. 1.2. configuration optimization
   3. 1.3. knowledge transfer
2. 2. intra-algorithms
   1. 2.1. ablation analysis
      1. 2.1.1. 解释
      2. 2.1.2. 例子
   2. 2.2. SHAP
      1. 2.2.1. 解释
      2. 2.2.2. 例子
         1. 2.2.2.1. 示例配置参数
         2. 2.2.2.2. 使用SHAP值解释配置对性能的影响
   3. 2.3. SMAC
      1. 2.3.1. 解释
      2. 2.3.2. 例子
         1. 2.3.2.1. 示例配置参数
         2. 2.3.2.2. 使用SMAC进行调优
   4. 2.4. RGPE
      1. 2.4.1. 解释
      2. 2.4.2. 例子
         1. 2.4.2.1. 示例配置参数（Knobs）
         2. 2.4.2.2. 使用RGPE进行调优
         3. 2.4.2.3. 具体例子
3. 3. experiments
   1. 3.1. general setup
      1. 3.1.1. hardware
      2. 3.1.2. workloads
      3. 3.1.3. tuning setting
   2. 3.2. knob selection
      1. 3.2.1. which importance measurement to use
         1. 3.2.1.1. 性能排名分析
         2. 3.2.1.2. 灵敏度分析
         3. 3.2.1.3. 结论
      2. 3.2.2. how many knobs to choose
         1. 3.2.2.1. 实验结果
         2. 3.2.2.2. 增量参数选择
   3. 3.3. optimizer selection
      1. 3.3.1. 不同大小配置空间的性能
      2. 3.3.2. 参数异构性的比较实验
      3. 3.3.3. 算法生成配置的开销
      4. 3.3.4. 总结

• Archive
• Tag
• Cate

Total : 67

2025

• 03/06 量化笔记

2024

• 10/29 automl-mfes-hb
• 09/21 knobs调优实验
• 09/05 knob-tuning
• 06/20 automl-paper-survey
• 03/18 回溯
• 03/14 最小生成树
• 03/09 动态规划股票买卖问题
• 03/06 栈与队列
• 02/29 双指针
• 02/07 动态规划背包问题
• 01/16 动态规划子序列问题

2023

• 12/17 HUST系统能力培养之虚拟机
• 11/27 heterogeneous graphs
• 11/18 Greenplum环境问题合集
• 11/12 HUST图神经网络Devign模型
• 11/11 graph neural network
• 11/10 message passing and node classification
• 11/09 node embeddings
• 11/07 traditional feature-based methods
• 09/13 Tsunami：a learned multi-dimensional index for correlated data and skewed workloads
• 09/11 PAT甲级2023夏真题
• 09/10 PAT甲级2018春真题
• 09/09 PAT甲级2017冬真题
• 09/07 PAT甲级2017秋真题
• 09/05 PAT链表笔记
• 09/03 PAT甲级2017夏真题
• 09/02 PAT算法杂烩笔记
• 09/01 PAT甲级2020秋真题
• 08/31 PAT甲级2020春真题
• 08/31 PAT甲级2017春真题
• 08/30 Learning Multi-dimensional Indexes
• 08/29 PAT甲级2016冬真题
• 08/26 PAT甲级2016秋真题
• 08/26 PAT并查集笔记
• 08/25 PAT甲级2016夏真题
• 08/21 PAT甲级2016春真题
• 08/20 PAT图笔记
• 08/19 Z-Order
• 08/13 PAT树笔记
• 07/26 Greenplum操作遇到的问题记录
• 06/29 Greenplum & PostgreSQL安装记录
• 04/30 HUST基于深度学习的三维重建
• 04/26 HUST大数据管理lab4教程
• 04/13 HUST大数据管理lab3教程
• 04/04 Slalom：Costing Through Raw Data via Adaptive Partitioning and Indexing
• 03/24 HUST大数据管理lab2教程
• 03/12 HUST大数据管理lab1教程
• 01/22 AutoMAP：Diagnose Your Microservice-based Web Applications Automatically
• 01/19 Lifelong Disk Failure Prediction via GAN-based Anomaly Detection
• 01/15 Minority Disk Failure Prediction Based on Transfer Learning in Large Data Centers of Heterogeneous Disk Systems

2022

• 11/20 Git其它用法补充
• 10/22 React笔记
• 10/17 Refs and the DOM
• 10/16 Webpack
• 07/29 18.四数之和
• 07/27 142.环形链表Ⅱ
• 07/24 15.三数之和
• 06/26 预训练语言模型
• 05/12 机器学习-集成学习
• 04/27 机器学习-支持向量机
• 04/23 机器学习-决策树
• 04/16 机器学习-线性模型

2021

• 04/15 数据结构-查找
• 03/30 虚拟机/服务器基础环境配置
• 01/05 托福学科单词

2020

• 12/22 欢迎来到我的博客

 计算机视觉  三维重建  深度学习  动态规划  查找  教程  MongoDB  数据库  Neo4j  MySQL  机器学习  GNN  database  托福  故障诊断  Greenplum操作  Linux磁盘扩容  debug记录  环境问题  多维索引  磁盘故障  迁移学习  列存分区  链表  LeetCode  双指针  剪枝  素数  逻辑题  并查集  树的遍历  哈希  字符串  排序  二叉搜索树  数学模拟  完全二叉树  最短路径  贪心  图论  Set  DFS  AVL树  图模拟  快乐模拟  栈  图的遍历  拓扑排序  递推  前端  React  Webpack  Eslint  top



 database  华科课程  算法  学习笔记  英语  腾讯AI训练营

