动态规划背包问题

算法动态规划

字数统计: 2.3k阅读时长: 9 min

 2024/02/07 

动态规划

借一下代码随想录的图

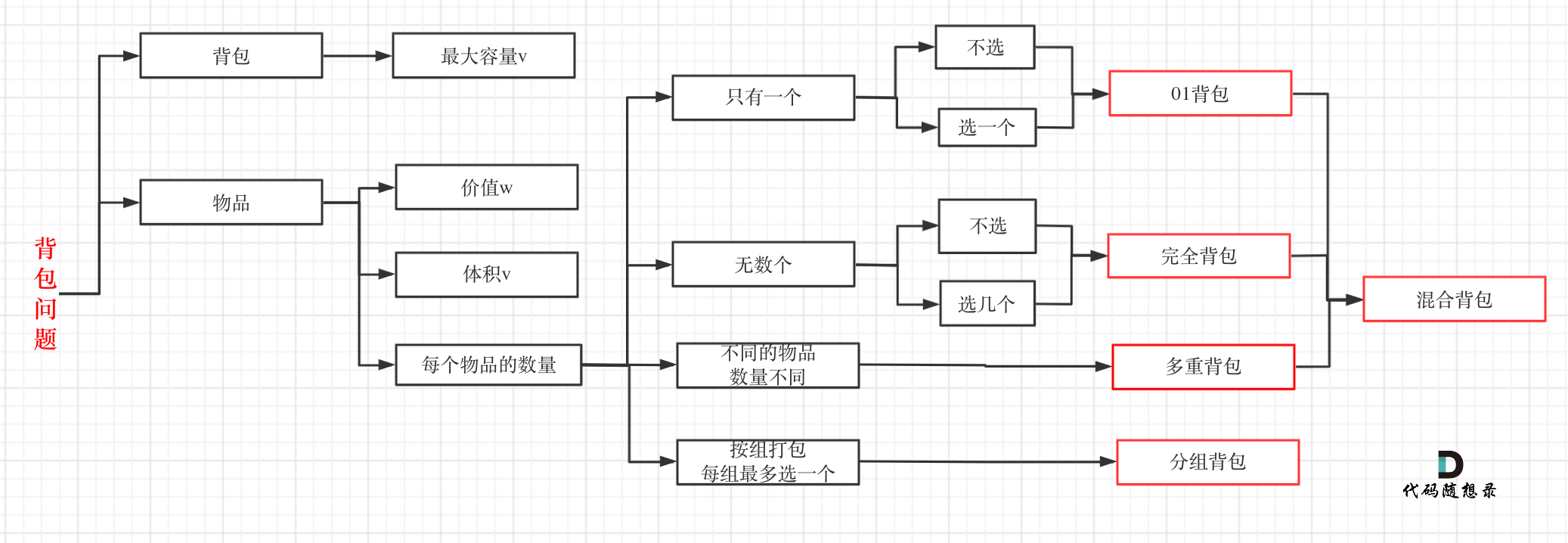
背包问题分类

01背包

[416] 分割等和子集

给你一个 只包含正整数 的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

解法

转换成01背包，背包的容量是sum / 2，要放入的物品的重量为nums数组元素的数值，价值也是其数值。如果背包正好装满则说明找到了总和为sum / 2的子集。

dp数组的含义 => dp[i]表示容量为j的背包可装入的最大价值为dp[j]

如果背包容量为target， dp[target]就是装满背包之后的重量，所以当 dp[target] == target 的时候，背包就装满了。

状态转移方程 => dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
初始化 => dp[0] = 0;
遍历顺序 => 外层物品内层背包容量，外层顺序内层倒序

// 模板
for(int i = 0; i < nums.size(); i++) {
  // 如果背包容量小于nums[i]，当前物品就装不下了
  for(int j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入，所以从大到小遍历
    dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
  }
}

代码

class Solution {
public:
  bool canPartition(vector<int>& nums) {
    int sum = 0;
    for (int i = 0; i < nums.size(); i++) sum += nums[i];
    if (sum % 2)  return false;
    sum /= 2;
    vector<int> dp(sum + 1, 0);
    for (int i = 0; i < nums.size(); i++) {
      for (int j = sum; j >= nums[i]; j--) {
        dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
      }
    }
    return dp[sum] == sum? true: false;
  }
};

[1049] 最后一块石头的重量Ⅱ

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎；
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

解法

一堆正的一堆负的，即一堆大的一堆小的。尽量两堆的重量相等所剩的质量才最小。

$\sum \limits ^{n-1} _{i=0}k_i ·stones[i] = (sum - neg) - neg = sum - 2 · neg$

要使最后一块石头的重量尽可能地小，$\textit{neg}$ 需要在不超过 $\textit{sum}/2 $ 的前提下尽可能地大。因此本问题可以看作是背包容量为 $\textit{sum}/2 $，物品重量和价值均为 $\textit{stones}[i]$的 0-1 背包问题。

代码

int sum = accumulate(stones.begin(), stones.end(), 0);
int target = sum / 2;
int n = stones.size();
vector<int> dp(target + 1, 0);
for (int i = 0; i < n; i++) {
  for (int j = target; j >= stones[i]; j--) {
    dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
  }
}
return sum - dp[target] - dp[target];

[494] 目标和

给你一个非负整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

解法

target = pos - neg = sum - 2 * neg

neg = (sum - target) / 2 => 背包容量

由于0 <= sum(nums[i]) <= 1000，-1000 <= target <= 1000，所以neg是非负整数，所以上式成立的前提是 sum - target 是非负偶数。

若上式成立，问题转化成在数组nums中选取若干元素，使得这些元素之和等于 neg（装满背包），计算选取元素的方案数，可以使用动态规划的方法求解。

dp[j] 代表填满容量为j的背包的方案数，只要搞到nums[i]，凑成dp[j]就有dp[j - nums[i]] 种方法。

代码

class Solution {
public:
  int findTargetSumWays(vector<int>& nums, int target) {
    int sum = accumulate(nums.begin(), nums.end(), 0);
    int diff = sum - target, n = nums.size();
    if (diff < 0 || diff % 2)  return 0;
    diff /= 2;
    vector<int> dp(diff + 1, 0);
    dp[0] = 1;
    for (int i = 0; i < n; i++) {
      for (int j = diff; j >= nums[i]; j--) {
        dp[j] += dp[j - nums[i]];
      }
    }
    return dp[diff];
  }
};

[474] 一和零

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的长度，该子集中最多有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的子集。

解法

求最大子集的长度，这里的物品是指每个strs里面的字符串（strs的类型为vector<string>），背包的容量是m和n，每个字符串的重量是其字符串中字符0和字符1的数量，每个字符串的价值为1。

注意这题不是完全背包，而是01背包，因为每个字符串只能用一次。

代码

class Solution {
public:
  int findMaxForm(vector<string>& strs, int m, int n) {
    // dp[i][j]代表有i个0和j个1的子集个数，这里m和n是背包的容量，只不过是二维的
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
    for (auto str: strs) {  // 遍历物品
      int n1 = 0, n0 = 0;
      for (auto ch: str) {  // 统计当前物品两个维度的重量
        if (ch == '0')  n0++;
        else  n1++;
      }
      for (int i = m; i >= n0; i--) { // 遍历第一维度的背包容量，倒序
        for (int j = n; j >= n1; j--) { // 遍历第二位维度的背包容量，倒序
          dp[i][j] = max(dp[i][j], dp[i - n0][j - n1] + 1);
        }
      }
    }
    return dp[m][n];
  }
};

完全背包

完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。

01背包内嵌的循环是从大到小遍历，为了保证每个物品仅被添加一次。而完全背包的物品是可以添加多次的，所以要从小到大去遍历，即：
1
2
3
4
5
6
// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
  for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
    dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
  }
}
组合数：先物品后容量；

排列数：先容量后物品。

[518] 零钱兑换Ⅱ

题目

代码

class Solution {
public:
  int change(int amount, vector<int>& coins) {
    vector<int> dp(amount + 1, 0);
    dp[0] = 1;
    for (int i = 0; i < coins.size(); i++) { // 遍历物品
      for (int j = coins[i]; j <= amount; j++) { // 遍历背包
        dp[j] += dp[j - coins[i]];
      }
    }
    return dp[amount];
  }
};

[377] 组合总和Ⅳ

题目

代码

正整数且不存在重复数字，找出和为目标整数的排列个数，可以用回溯暴力搜

这里的数字又可以重复使用，而且只要排列的个数不需要将每个答案都列出来，因此可以用动态规划进行优化。是一个完全背包问题。

物品是数组里的元素，背包的重量和价值是元素之和，背包容量是target。

dp[j] 表示目前重量为j的背包里装的方法排列个数，因此 dp[0] 要初始化为1，虽然 dp[0] = 1 是没有任何意义的，只是为了进行递推。

排列数外层是背包重量，且内层从小到大；内层是物品。

C++测试用例有两个数相加超过int的数据，所以需要在if里加上dp[j] < INT_MAX - dp[j - nums[i]]。

int n = nums.size();
vector<int> dp(target + 1, 0);
dp[0] = 1;
for (int j = 0; j <= target; j++) {
  for (int i = 0; i < n; i++) {
    if (j - nums[i] >= 0 && dp[j] < INT_MAX - dp[j - nums[i]]) {
      dp[j] += dp[j - nums[i]];
    }
  }
}

[70] 完全爬楼梯

题目

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

输入描述：输入共一行，包含两个正整数，分别表示n, m

输出描述：输出一个整数，表示爬到楼顶的方法数。

代码

物品是 1 ~ m 共m个整数，背包容量是n，且是排列数

#include <bits/stdc++.h>
using namespace std;

int main() {
  int n, m;
  cin >> n >> m;
  vector<int> dp(n + 1, 0);
  dp[0] = 1;
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
      if (i - j >= 0)	dp[i] += dp[i - j];
    }
  }
  cout << dp[j] << endl;
  return 0;
}

[322] 零钱兑换

题目

代码

Next Post

双指针
Previous Post

动态规划子序列问题