cs224w课程学习笔记
$G=(V,E,R,T)$
node type $T(v_i)$, relation type $r \in R$
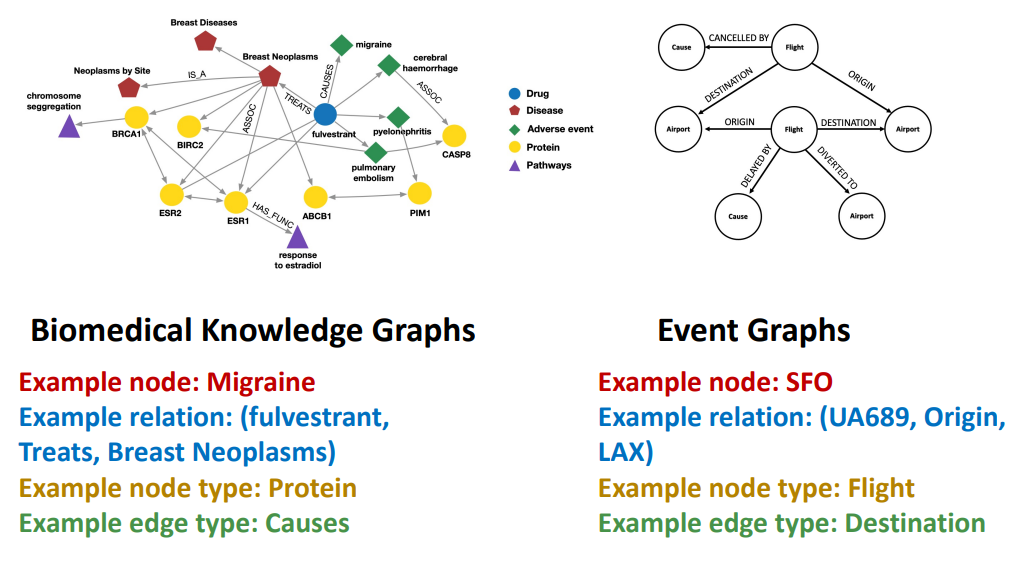
RGCN
extend GCN to handle heterogeneous graph with miltiple edge/ relation types
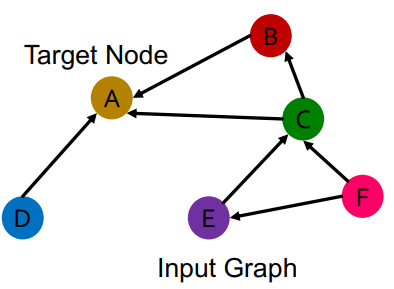
we should use different neural network weights for different relation types
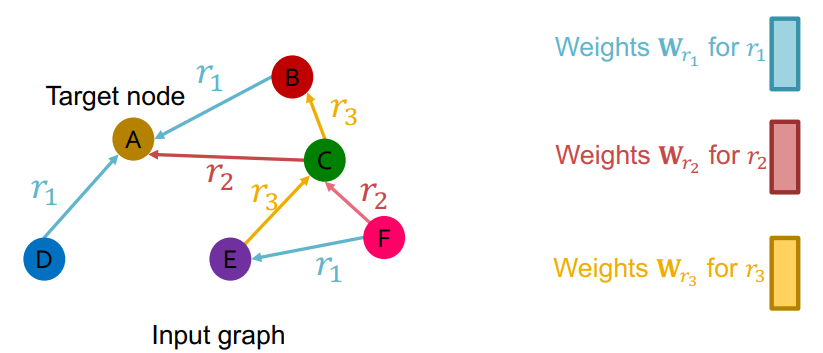
$$h^{(l+1)} _v = \sigma(\sum \limits _{r \in R} \sum \limits _{u \in N^r _v} \frac{1}{c _{v,r}} W^{(l)} _r h^{(l)} _u + W^{(l)} _0 h^{(l)} _v)$$
message
each neighbor of a given relation:
$$m^{(l)} _ {u,r} = \frac{1}{c_{v,r}} W^{(l)} _r h^{(l)} _u$$
self-loop:
$$m^{(l)} _v = W^{(l)} _0 h^{(l)} _v$$
aggregation
sum over messages from neighbors and self-loop, then apply activation
$$h^{(l+1)} _v = \sigma(Sum({ m^{(l)} _{u,r}, u \in {N(v)} \cup { v } }))$$
scalability
如果有L层,那么对于每个关系就会有L个权重矩阵: $W^{(1)} _r, W^{(2)} _r…W^{(L)} _r$
而每个权重矩阵的大小 $W^{(l)} _r$ 是 $d^{(l+1)} \times d^{(l)}$
每个矩阵都有不同的尺寸,且随着类型以及隐藏层的数目增加,参数会呈现指数级的增长,模型就会变得太大,会出现过拟合以及无法训练的问题
how to reduce or regularize?
- use block diagonal matrices
- basis/dictionary learning
block diagonal matrices
key:减少非0元素数量 => 训练地更快,模型更robust,不容易过拟合
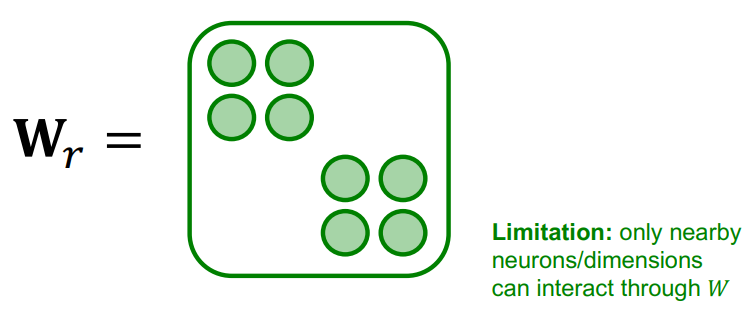
用B个低维矩阵,参数从$d^{(l+1)} \times d^{(l)}$减少到$\frac{d^{(l+1)}}{B} \times \frac{d^{(l)}}{B}$
只有相邻神经元/嵌入维度可以通过权重矩阵交互,要解决这一限制,需要多加几层神经网络,或者用不同的block结构,才能让不在一个block内的维度互相交流。
解释一下这是为什么
这个做法就是让把大矩阵给切成小块,比如原来的100×100按稀疏程度刚好能切成四个25×25的,设想以下场景:原来有23号和41号相连,但因为分区的存在23号只能和0号至24号交换信息,这就是所谓“只有同一个块里相邻的神经元才能交互”的意思。
basis learning
key:在不同的关系中共享权重
将每个关系的权重矩阵表示为基变换的线性组合
$$W_r = \sum^{B} _ {b=1} a _ {rb} \cdot V_b$$
这里$V_b$是共享的权重矩阵,$a_{rb}$是系数,这样我们就只需要训练和学习${ a_{rb} }^B _{b=1}$ 就行
example: entity/ node classification
如何定义各种任务?
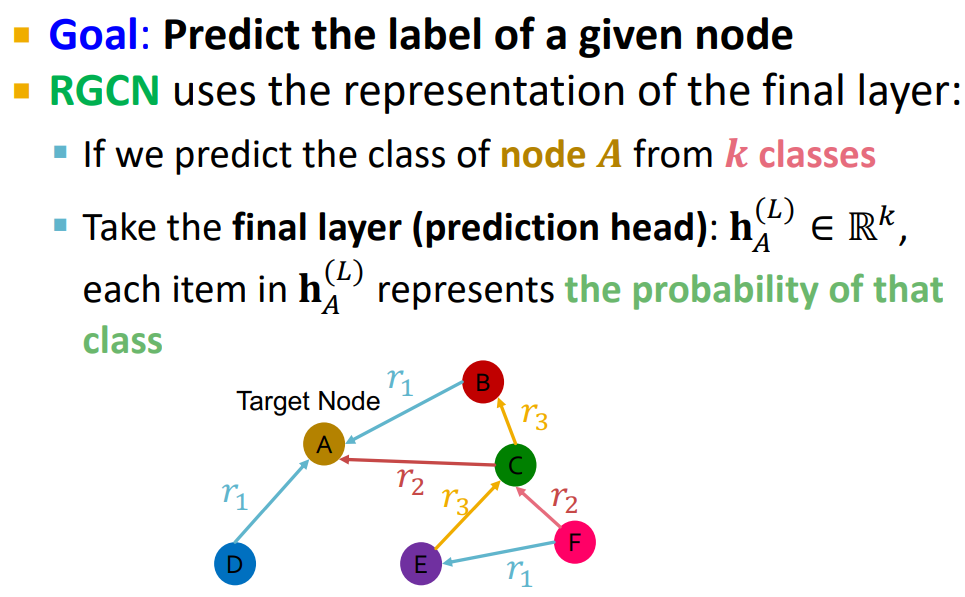
dataset splitting
将每种关系对应的边都分成 training message edges, training supervision edges, validation edges, test edges 四类
=> 解决样本不平衡的问题,如果不先做边的分类直接将所有类型的边混在一起分成四份,无法保证四个数据集里含有所有关系类型的边
这么分完最后再合并到一起,合成大的四类
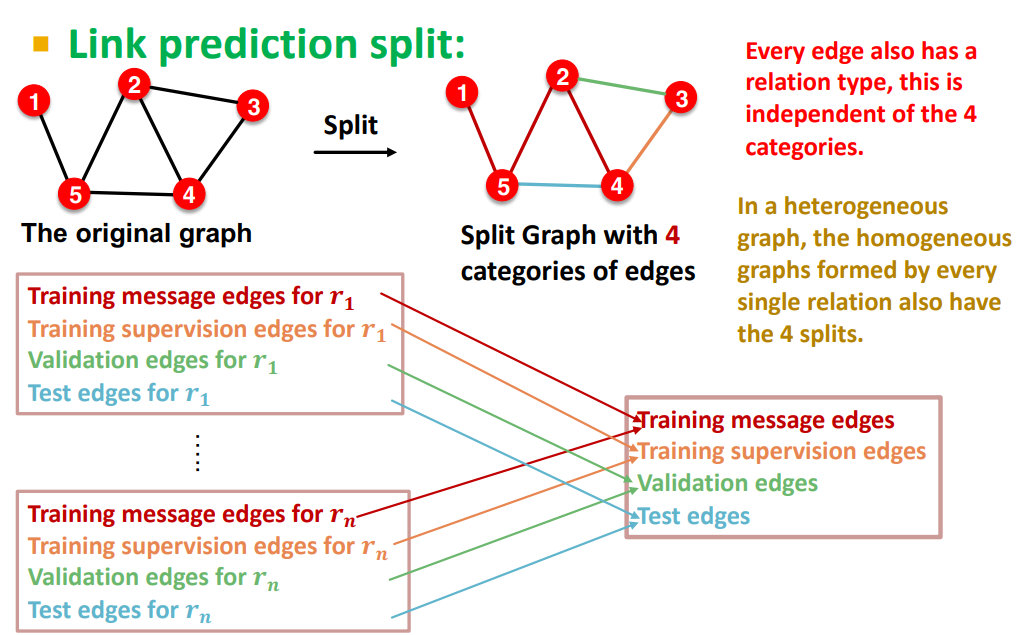
假设$(E,r_3,A)$是training supervision edge,其它所有的边都是training message edges。我们取E和A最后一层的embedding:$h^{(L)} _ E$和$h^{(L)} _ A$,然后使用一个函数$f_r: \mathbb{R}^d \times \mathbb{R}^d \to \mathbb{R}$来计算二者有关联的概率。例如 $f_{r1}(h_E,h_A)=h^T_E W _{r1} h_A, W _{r1} \in \mathbb{R}^{d \times d}$
training
negative edge的概念
既不属于training edges也不属于training supervision edges的边
用training message edges来预测training supervision edges
找到training supervision edges,比如图中的 $(E,r_3,A)$,用RGCN来对其打分(score)
增加一个negative edge来干扰supervision edge,因为这里supervision edge是从E到A的$r_3$类型的边,那么图中我们就可以增加$(E,r_3,B)$或者$(E,r_3,D)$或者$(E,r_3,F)$.
增加完negative edges之后我们也用RGCN来给其打分
使用交叉熵损失函数来优化,损失函数如下:
- 最大化training supervision edges的分数
- 最小化negative edges的分数
$$\mathscr{l} = -log \sigma(f _{r3}(h_E,h_A)) - log(1-\sigma(f _{r3}(h_E,h_B)))$$
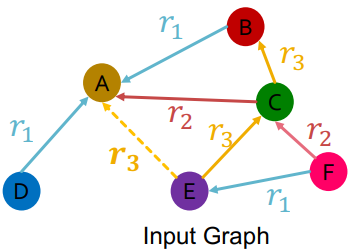
evaluation
因为在training的时候我们已经minimize了negative edge $(E,r_3,B)$的分数了,所以直觉上我们要预测的边$(E,r_3,D)$即validation edge的分数应该要比上面minimize score的negative edge高
用training supervision edges和training message edges来预测validation edges
- 用RGCN计算$(E,r_3,D)$分数
- 计算其它negative edges的分,在这里是${ (E,r_3,v) \mid v \in { B,F }}$
- 将以上的分数排序,获得$(E,r_3,D)$的排名RK,有两种指标:
- Hits@k: $1\space [RK \leq k]$,表示最后返回的前k个结果中命中的次数,因此命中次数越大越好;
- Reciprocal Rank:$\frac{1}{RK}$,取倒数,排名越小越好,因此倒数越大越好.
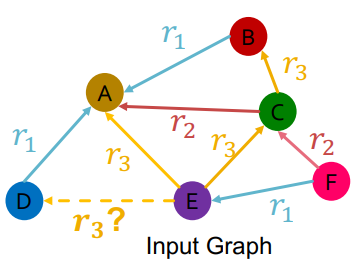
Knowledge Graphs Completion
embedding
shallow embedding
知识图谱中的边用一个三元组来表示$(h,r,t)$,节点头$h$和节点尾$t$有关系$r$,模型实体和关系都属于嵌入空间 $\mathbb{R}^d$
给定一个三元组,我们的嵌入目标是让$(h, r)$的嵌入向量接近$t$的嵌入向量。
- 如何embed$(h, r)$
- 如何定义接近度
最简单最自然的想法是transE:
- 给定一个$(h,r,t)$,如果两点之间关系存在,则$h+r\approx t$;反之$h+r ≠ t$
- 得出$f _r (h, t) = - \mid \mid h + r - t \mid \mid$
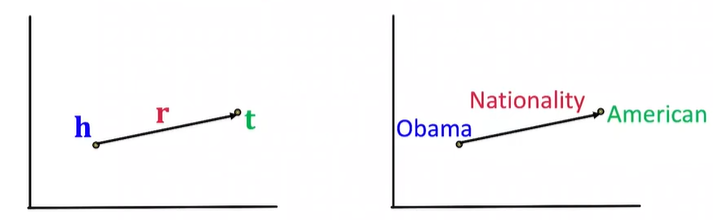
transE算法
1 |
常见关系:
对称关系
- $r(h, t) => r(t, h)$
- 你是我室友我也是你室友这叫对称
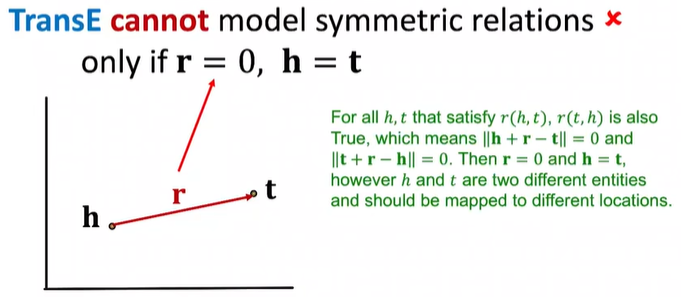
反对称关系
- $(r(h,t) => \neg r(t,h))$
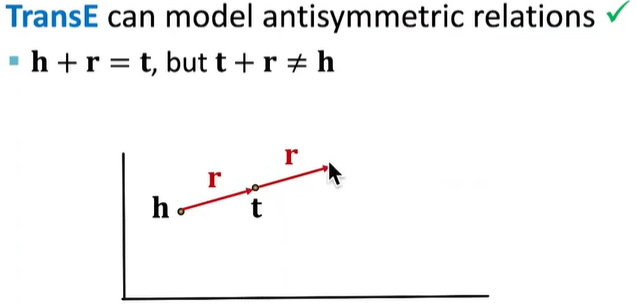
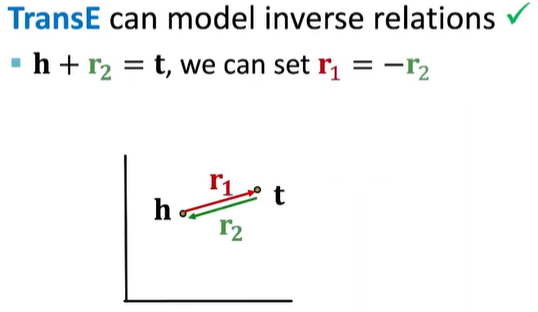
逆关系
- $r_2(h,t) => r_1(t,h)$
- 雇佣和被雇佣
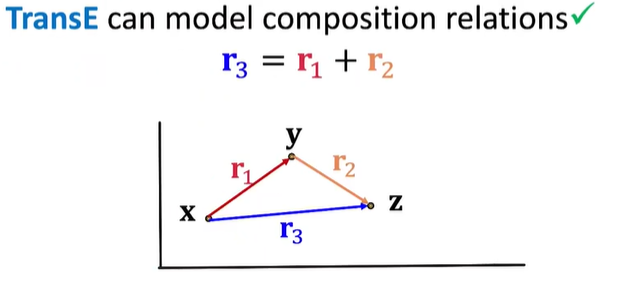
复合传递关系
- $r_1(x, y) \land r_2(y,z) => r_3(x,z)$ $\forall x,y,z$
- 我妈的老公是我爹:我和我妈是母女关系,我妈和某个人是夫妻关系,那么我和这个人是父女关系
一对多关系
- $r(h,t_1),r(h,t_2),…,r(h,t_n)$都为真
- 一个老师可以有多个学生,$t1,t_2,…,t_n$都是学生

注意这里的反对称关系和传递性和离散数学里的定义有些不同,别搞混