图机器学习学习笔记
deep learning for graphs
图网络要复杂得多:
- 尺寸任意,拓扑结构复杂
- 没有固定的节点顺序或参考点
- 通常是动态的,具有多模态特征
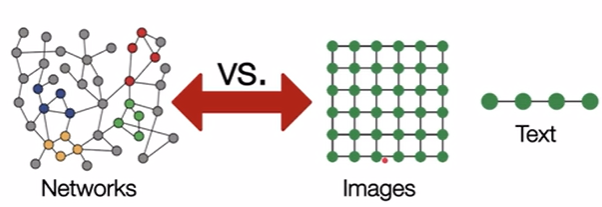
将ajacency matrix和node feature结合送入网络存在以下问题
- $O(\mid V \mid)$参数太大
- 不适用于不同大小的图
- 对节点排序敏感
如果套用CNN的话,没有固定的notion of locality或者sliding window在一个卷积核内,以及graph的同构性从不同角度看会不一样但图是permutation invariant的
permutation invariance / equivariance
- 置换不变性
- 对于图嵌入
- 节点的排序不会改变图的表示
- 排列不变性
- 对于节点嵌入
- 节点的排序将导致节点表示的相同排序
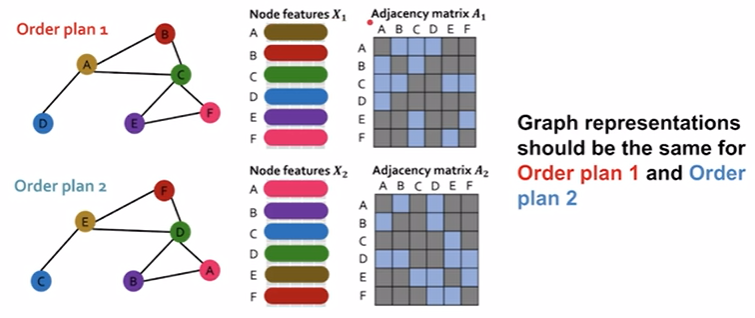
对于上面的两个图,embedding函数$f(Ai, Xi)$产生的结果应该是一样的,这样的函数就说其是permutation invariance
Graph neural networks consist of multiple permutation equivariant / invariant functions.
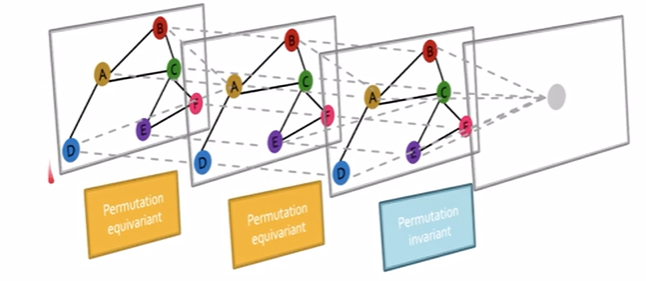
a general perspective on graph neural network
如果借用CNN的思维的话即从邻居那得到咨询然后做卷积,这种即GCN。我们需要定义邻居以及让模型学会如何得到邻居的信息(aggregate infomation)
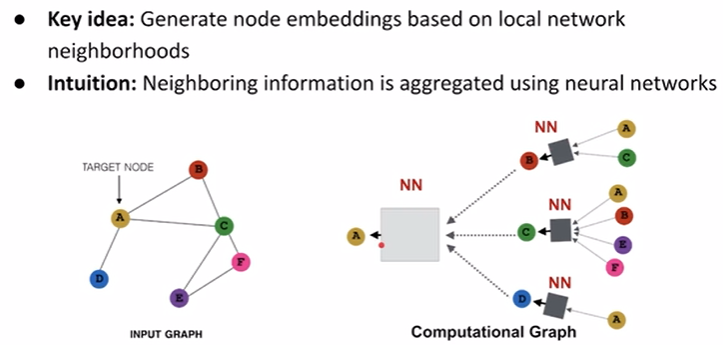
receptive field在cnn里指的是卷积核的视野,在graph里是指拉neighbors的次数,一阶邻居、二阶邻居,receptive field越大能看到的范围越大。当邻居的info拿到后要做平均,然后使用一个nn做更新。
math of graph convolution
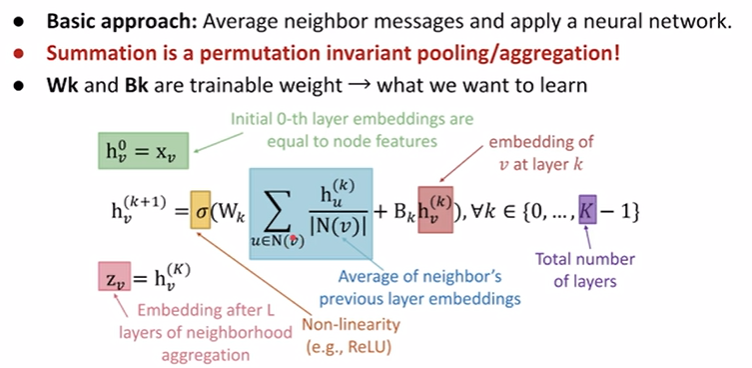
$h^{(k)}_u$ 是node-v邻居的embedding,加起来除以邻居的数量,即蓝色部分是在平均邻居的咨询。而这样缺少了自身的咨询,因为要加上红色部分node-v本身的咨询 $h^{(k)}_v$。注意加上前需要分别乘上weight进行transform,得到和后使用非线性函数激活。这样就是一次的convolution即1-layer(注意这里因为permutation invariance / equivalence所以拉邻居的顺序不会影响最后的结果)
但当graph的node很多的时候复杂度会很高,因此我们需要借助matrix operation
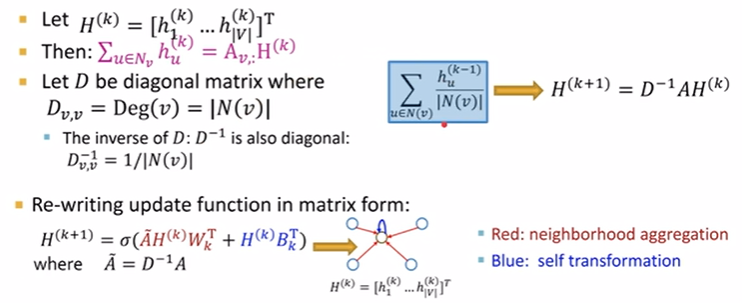
matrix formulation
拉邻居加起来的过程就可以看作是邻接矩阵乘上embedding matrix,在用度矩阵degree做一个平均。
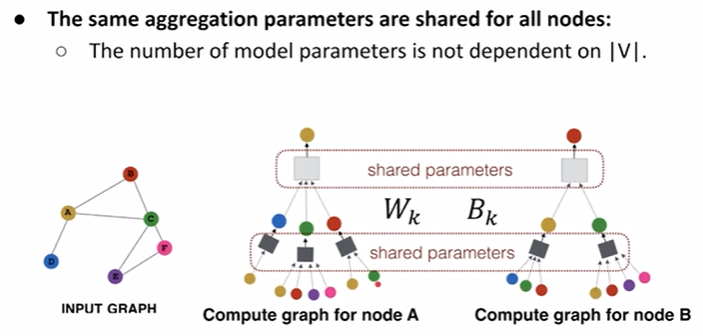
gnn framework
gnn layer = message + aggregation,现在不同的gnn的区别是他们产生message的方法或者aggregate的方法不同;
借由叠加多层的layer,看到的视野更大,而不同的层数之间也可以像cnn一样使用dropout来更powerful;
有时候一个graph可能本身没有feature只有一个结构,又或者是graph的结构太复杂/稀疏,我们可以做feature augmentation / structure augmentation,即raw input graph ≠ computational graph.
learning objective: Supervised / Unsupervised objectives, Node/Edge/Graph level objectives;
inductive capability
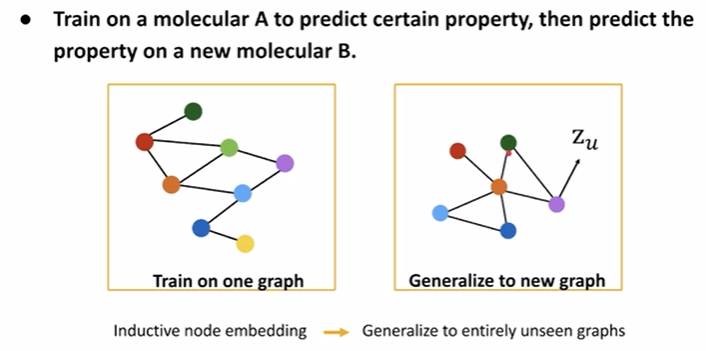
a single layer of a gnn
theory
message function
message function是在对邻居的node embedding做一些转换,让它更好再传给当前node
$m^{(l)}_u = MSG^{(l)}(h^{(l-1)} _ {u})$
这里的$MSG$可以是任何形式的layer,可以是linear也可以是non-linear,甚至可以是multi-layers的
aggregation function
收集所有邻居的info,可以用sum、mean等。
$$h^{(l)}_v = AGG^{(l)}({m^{(l)}_u, u \in N(v)})$$
$$AGG: Sum(·),Mean(·),Max(·) $$ 优势从左到右以此递减
message agregatio issue
上述的单一message+aggregation方法缺失了node-v自己的值
$$h^{(l)} _v = CONCAT(AGG({ { m^{(l)} _u, u \in N(v} }), m^{(l)} _v)$$
写成带学习权重的形式就是:
$$m^{(l)} _u = W^{(l)}(h^{(l-1)} _ {u})$$
$$m^{(l)}_v = B^{(l)}(h^{(l-1)} _ {v})$$
整个过程就是:
$$h^{(l)} _v = CONCAT(AGG({ { W^{(l)}(h^{(l-1)} _ {u}), u \in N(v} }), B^{(l)}(h^{(l-1)} _ {v}))$$
examples
GCN
$$h^{(l)}_v = \sigma (W^{(l)} \sum\limits _ {u \in N(v)} \frac{h^{(l-1)}_u}{\mid N(v) \mid})$$
$$h^{(l)}_v = \sigma (\sum\limits _ {u \in N(v)} W^{(l)} \frac{h^{(l-1)}_u}{\mid N(v) \mid})$$
变换后就是
$$h^{(l)} _v = \sigma(Sum({ { m^{(l-1)} _ {u}, u \in N(v) } } ))$$
注意转换后的公式,把w移动进去后,把邻居的message即$h^{(l-1)}_u$乘上一个learning weight,再除以node的degree做一个平均normalize,这是message部分。然后在用一个$Sum(·)$做一个aggregation。最后包一层non-linear的layer。
GCN解决丢失自己node embedding的issue时,在图里添加了一个self-edges即loop,使得邻接矩阵添加了一个单位矩阵$I$。
如果写成矩阵计算的形式就是:
$$A’ = A + I$$
$$\hat{A} = D^{-\frac{1}{2}}A’D^{-\frac{1}{2}}$$
$$H^{(l)} _v = \sigma(\hat{A} H^{(l-1)} _v W^{(l)})$$
GAT
$$h^{(l)} _ v = \sigma (\sum\limits _ {u \in N(v)} \alpha_{vu} W^{(l)} h^{(l-1)}_u)$$
这里的$\alpha_{vu}$是attention weights,也是通过学习得到的。
- 在GCN里,$\alpha_{vu} = \frac{1}{\mid N(v) \mid}$即对于某个node所有的邻居都是一个固定的权重,所有的邻居都是同等重要。
procedure
假设$e_{vu}$代表了node-u和node-v之间的重要性,$a(·)$是一个计算机制,喂入的是两个node的embedding吐出来的是一个importance,计算公式为:
$$e_{vu} = a(W^{(l)}h^{(l-1)}_u, W^{(l)}h^{(l-1)}_v)$$
然后再用softmax函数做normalize,使得所有邻居的$e_{vu}$相加的和为1:
$$e_{vu} = \frac{exp(e_{vu})}{\sum\limits_{k\in N(v)}exp(e_{vk})}$$
这里的$e_{vu}$就是最后的$\alpha_{vu}$
about $a(·)$
是一个独立的机制,怎么做都可以,可以把两个embedding拿去concatenate起来过一个linear或者其它。不管怎么样,它都和前面的message的$W$是独立的,即train jointly。
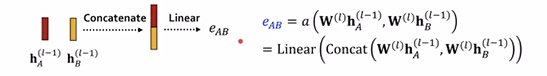
multi-head attention
像transformer一样,对于单个node可能会学多组$\alpha$,再对这些做一个aggregate
$$h^{(l)} _v[1] = \sigma(\sum _{u \in N(v)} \alpha^1 _{vu}W^{(l)} h^{(l-1)} _u)$$
$$h^{(l)} _v[2] = \sigma(\sum _{u \in N(v)} \alpha^2 _ {vu}W^{(l)} h^{(l-1)} _u)$$
$$h^{(l)} _v[3] = \sigma(\sum _{u \in N(v)} \alpha^3 _{vu}W^{(l)} h^{(l-1)} _u)$$
$$h^{(l)} _v = AGG(h^{(l)} _v[1], h^{(l)} _v[2], h^{(l)} _v[3])$$
最经典的图就是这张:
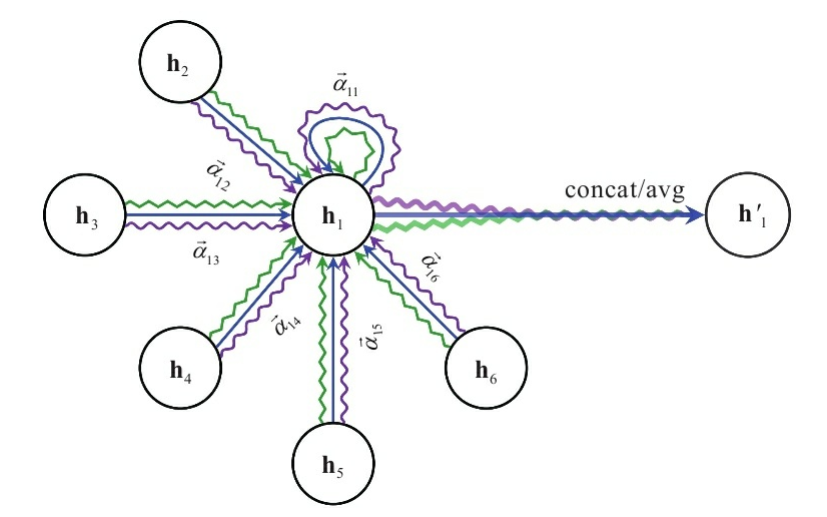
benefits of attention mechanism
使不同邻居具有不同重要性
计算可以并行化,效率高
参数的数量与图的大小无关
可以推广到不同的图
a gnn layer in practice

graph augmentation for GNNs
why
- 图特征增强图形
- 输入缺少特征
- 图结构扩充
- 图过于稀疏→消息传递效率低下
- 图太密集→消息传递成本太高
- 图太大→内存容不下
feature augmentation
只有邻接矩阵没有node feature
- 加上人工的feature,加上constant values to nodes
- 给node编号并转换成one-hot vector
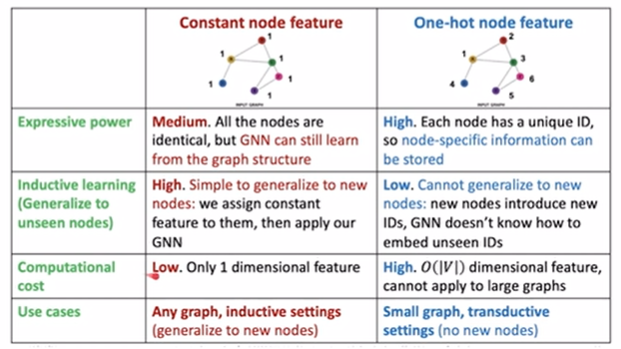
structure augmentation
virtual nodes / edges
graph很稀疏时


neighborshood sampling
graph很密集的时候
大幅度降低计算cost和memory cost
data splitting for graphs
graph的切法比较tricky,因为在graph里数据(邻居关系)是互相依赖的。
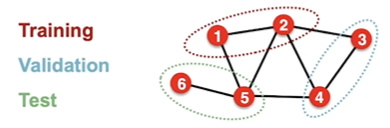
solutions
transductive seeting
不改变graph架构,但是train的时候只用部分node的标签,剩下的node的label用来validation/test
inductive setting
会把graph切成不同的部分,改变graph的结构
compare
transductive
- 在同一图上
- 通常在单图数据集上执行
- 只有标签被分割适用于节点/边缘预测任务
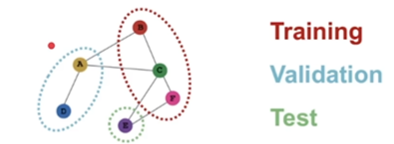
inductive
- 通常在多图数据集上执行
- 节点/边/标签被分割
- 适用于节点/边/图任务
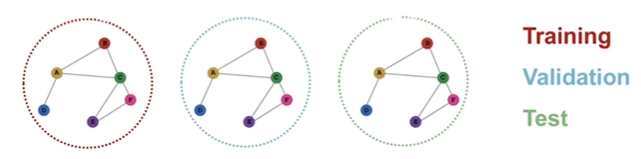
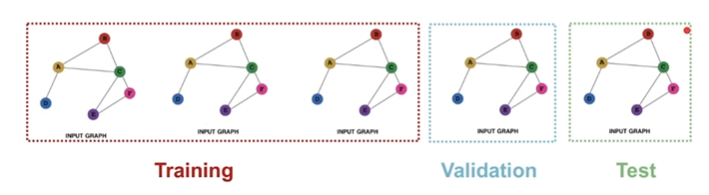
examples
graph classification
比较适合使用inductive setting
link prediction
是unsupervised或者self-supervised
inductive
通常把某些edge隐藏起来,因此edge被分为两种:1)message edges 用于message passing 用于喂给GNN;2)supervision edges 用于最后预测,计算loss
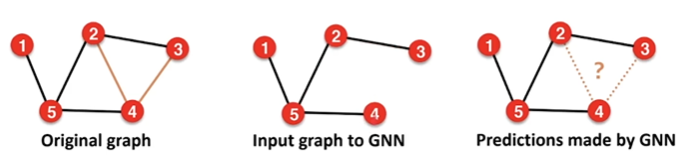
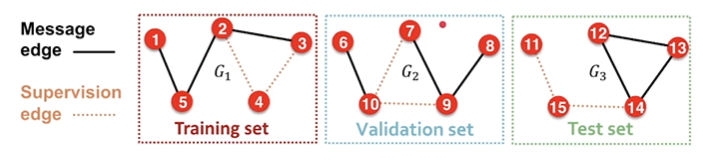
transductive
通常把edge分为四种
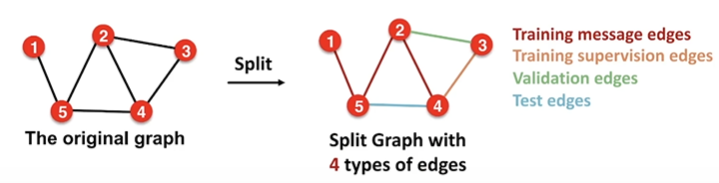
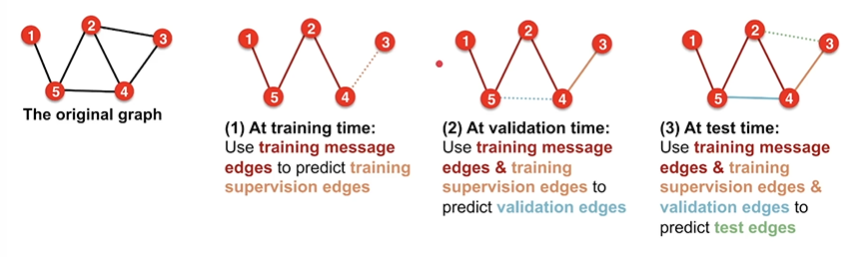
summary
- node-level task
- inductive/transductive settings
- graph-level task
- inductive settings
- edge-level task
- inductive/transductive settings