图机器学习学习笔记
introduction
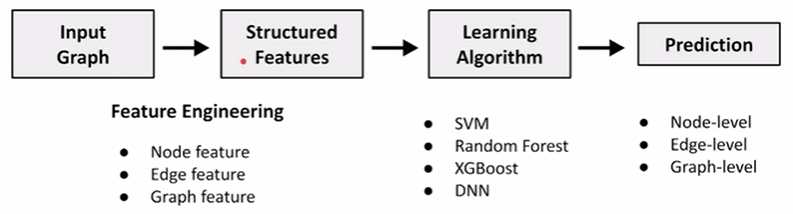
用graph representation learning的方式代替人工的feature learning过程,即learn the features by itself
我们的最终目的是学习到一个efficient features,它是task-independent的。我么需要一个encode的部分,将graph的node map到一个dimension,map过去可以保留node之间的similarity
- 类似nlp里面word的embedding完,原本比较接近的word在map之后也是比较接近的
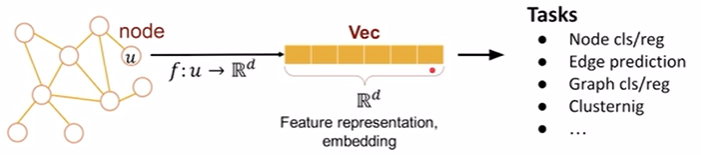
encode nodes => similarity in embedding space (dot product) ≈ similarity in the original graph
- 编码器:节点 => 嵌入(d维向量,$ENC(v) = z_v$)
- 解码器:嵌入 => 相似度评分(点积)
- 定义节点相似度函数:2个节点是否接近,接近程度如何?
- 优化 => $similarity(u,v)≈z^{T}_{v} z_u$
通过shallow encoding查表得方式,为每个节点被分配一个唯一的嵌入向量,优化embedding以最大化每个相似节点对(u, v)的$similarity(u,v)≈z^{T}_{v} z_u$。
如何定义节点相似度? 两个节点连接在一起? 他们共用邻居? 他们有相似的结构角色?=> 随机漫步
random walk approaches for node embeddings
两个优点:
- expressively:random walk的方法可以增大视野,可以使当前的node看到离当前比较远的nodes的信息
- efficiently
feature learning as optimization
log-likelihood objective
$$max \sum{log P(N_R(u) \mid z_u)}$$
对于每个node节点u,从u开始做random walk,对于其经过的邻居$N_R(u)$,他们的相似程度是比较高的,而非邻居节点他们的similarity是比较低的。
loss function
$$\mathcal{L} = \sum\limits_{u \in V}{\sum\limits _ {v \in N_R(u)} -log(P(v\mid z_u))}$$
$$P(v \mid z_u) = \frac{exp(z^{T} _ {u}z_v)}{\sum\limits _ {n \in V} exp(z^{T} _ {u}z_n)}$$
因为要最大化邻居之间的相似度,log取负之后就是最小,最后minimize这个loss function即可。下面那个公式是softmax,转换成一个sum为1的机率分布,先去计算node u到其它每个node之间的similarity作为分母,分子是他的neighbors。
要计算每个node-u的similarity,时间复杂度是$O(\mid V^2\mid)$
为了方便计算我们将softmax的exp改写成sigmoid,且分母不再计算所有node,而是进行sample,采样的个数k=5~20,k越大robust extant越高。
stochastic gradient descent
sample、更新gradient

node2vec
deepwalk都假设走一个固定长度的length,每一步都随机选择unbiased。但这种方法not rich enough to embed nodes from same network community as well as nodes with similar structural roles,即我们希望能关心到同一个community里类似的node以及远方类似结构的community
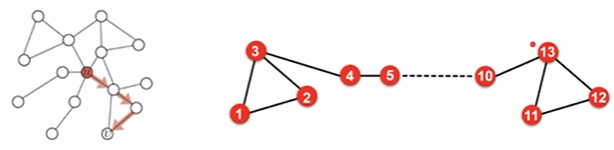
设计一个biased的random walk,有意识地决定我们要走的方向,并关注similar network neighborhood,可以trade off between local and global views of the network.
two classic strategies to define a neighborhood $N_R(u)$ of a given node u: 1)BFS, 2)DFS
biased 2nd-order
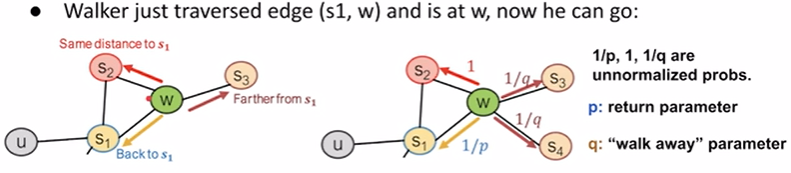
如果我今天想走local的就采用bfs策略,我们就把p的值调小,1/p机率就更大;但如果我们今天想去远方,我们就采用dfs策略,就把q的值调小,1/q的概率就更大,更容易往远方走。
algorithm
- Compute random walk probabilities
- Simulate rrandom walks of length Istarting from each node u
- Optimize the node2vec objective using stochastic gradient
applications and limitations of shallow encoding
usage

limitations
- 遇到很大的graph参数量会爆炸,因为每个node都会有自己的embedding而且每个embedding之间不会有shared的参数
- 出现一个新的graph就要重新跑一次random walk,即没法运用现在学到的node embedding => inherently transductive
- node的feature没法考虑进去,即只能考虑node与node之间的connectivity
transductive vs. inductive learning
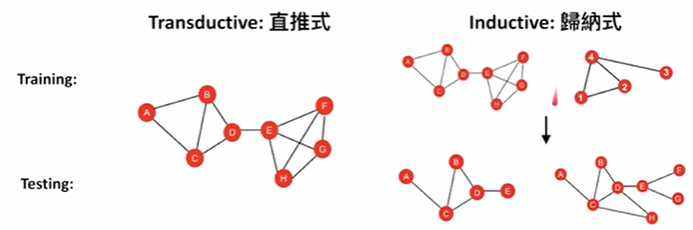
在transductive learning中,对于新的图,我们必须从头开始训练embedding的。然而,inductive可以将我们目前学到的embedding直接应用到新的graph上面来求得它的node embedding。
inductive learning on graphs => deep encoder => gragh neural network