图机器学习学习笔记
node, edge, graph-level prediction
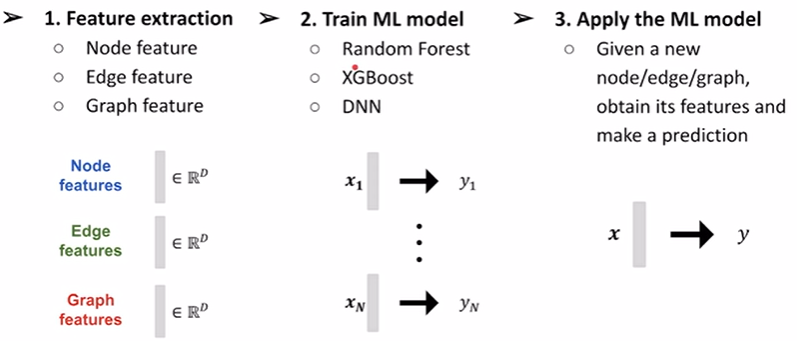
feature design是非常重要的部分
1) node-level prediction
node的feature的表示方法分为importance-based和structure-based两种;
- importance-based 捕获图中节点的重要性,用于预测图中有影响的节点
- node degree
- node centrality
- structure-based 捕获节点周围的局部邻域的拓扑属性,对于预测节点在图中扮演的特定角色非常有用
- node degree
- clustering coefficient
- graphlets
importance-based
degree
用度来衡量
centrality
节点度仅计算该节点的邻居,而无法确认节点的重要性或标识这个节点,因此我们需要使用一个叫做中心度的指标来衡量一个节点的重要性。
engienvector centrality
如果被重要的相邻节点$u$包围,则节点$v$是重要的,将节点$v$的中心性建模为相邻节点的中心性的递归和(因为$c_v$用$c_u$来计算,但是$c_u$也是用$c_v$计算)
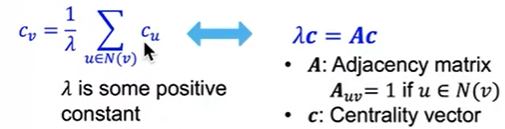
betweenness centrality
一个node如果坐落在很多最短路径上,说明它很重要

closeness centrality
如果一个node到其它node最短路径都很近的话,说明它很重要,分母是他到别的node的最短路径之和。

structure-based
clustering coefficient
分子是它的邻居两两相连的个数,分母是邻居节点对个数
寻找三角形的个数(三角关系:我朋友的朋友之后也会是我的朋友)
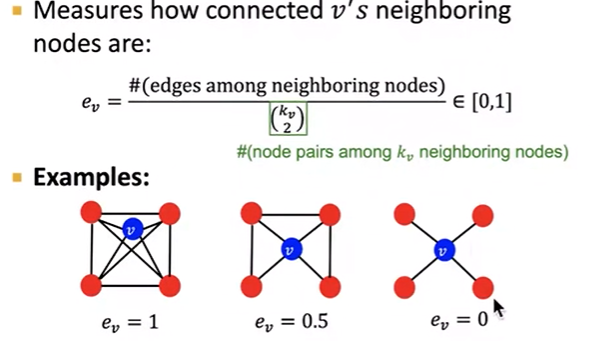
graphlet
graph isomorphism
isomorphism表示具有相同数量的顶点、边和相同的边连通性(同构图、等价图)
简而言之就是扭来扭去之后其实是一样的
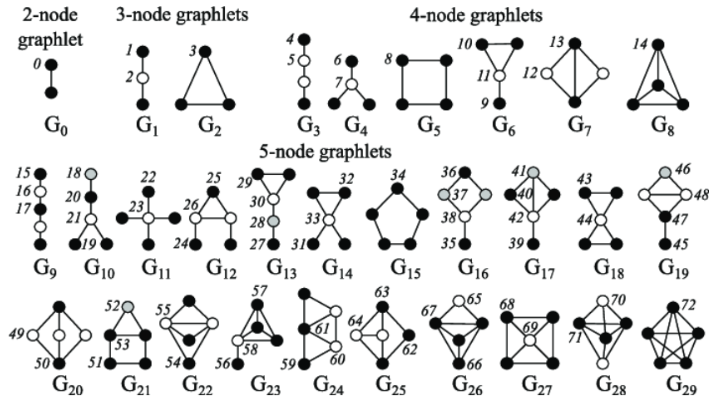
Graphlets are induced, non-isomorphic subgraphs that describe the structure of node u’s network neighborhood
induced subgraph表示取出两个node对时要把它们俩的边关系也取出来
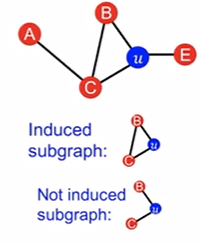
u这个node,u-B还有u-E还有u-C的关系都属于$G_0$,a-c-u关系属于$G_1$,以此类推;所以u包含的graphlets有[0, 1, 2, 3, 5, 10, 11]
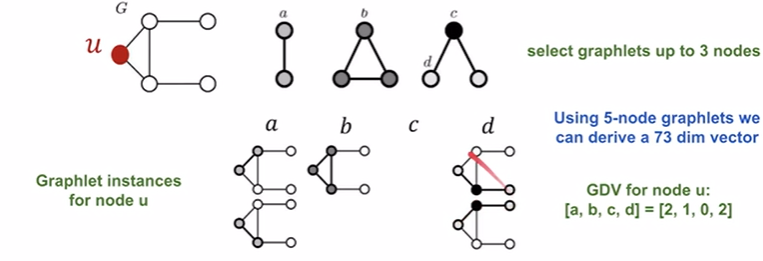
Graphlet Degree Vector (GDV) :A count vector of graphlets rooted at a given node.
提供了一个节点的本地网络拓扑的度量(比节点度或聚类系数更详细)。
- 示例如下:注意这里c的个数为0是因为必须是induced的
2) edge-level prediction
node与node之间是否存在edge? node与node之间edge的权重是多少?
Distance-based features
Local neighborhood overlap
Global neighborhood overlap
distance features
shortest-path distance between two nodes
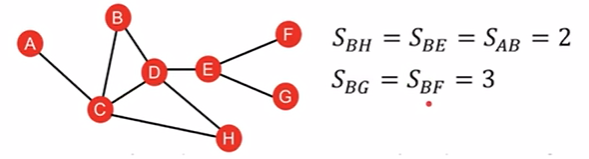
问题在于:会没办法区分shortest path一样的node,比如图上的BE和BH
local neighborhood overlap
缺点是视野很小
common neighbors
单纯计算两个node之间的共同neighbor个数,来衡量两个node之间的紧密程度
Jaccard’s coefficient
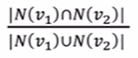
相比common neighbors优势在于,可以看到占比,即common neighbors多也有可能是因为两个node本来身边的neighbors就很多
Adamic-Adar index
计算两个node的共同的邻居的degree取log取倒数再相加,即共同邻居的degree越大,最后得到的权重value越小
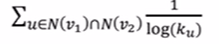
global neighborhood overlap
希望能看到更大的视野
Katz index
先计算点对之间所有长度路径的条数,一般的方法是先用邻接矩阵的幂次方来计算,k次方就代表了节点对之间长度位k的路径的条数,最后根据length的长度从1到无穷每个乘上一个系数并加起来。
衡量一个node是否处在一个比较发达/偏僻的地方。

3) graph-level prediction
前两次是如何去较好地表示node和edge的feature的表达方式
图级别特征构建目标:找到能够描述全图结构的特征,让比较相似的两个graph定义得到的feature的similarity是比较高的。
找到一个函数$\phi$,把graph表示为一个vector的representation,最后两个graph的similarity可以由两个$\phi$函数的内积计算得到.
所以我们的目标是设计一个bgraph kernel $\phi(G)$
bag-of-Words
在NLP中,BoW将单词在文档中的频率作为特征来计算。
最简单的方法:将节点视为单词
下图中这样设计出来的$\phi$的结果都是4,这两个graph是相同的
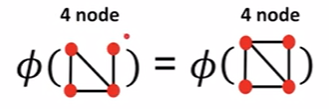
bag-of-degrees

graphlet features
在这里看graphlet是基于整个graphlet的视野
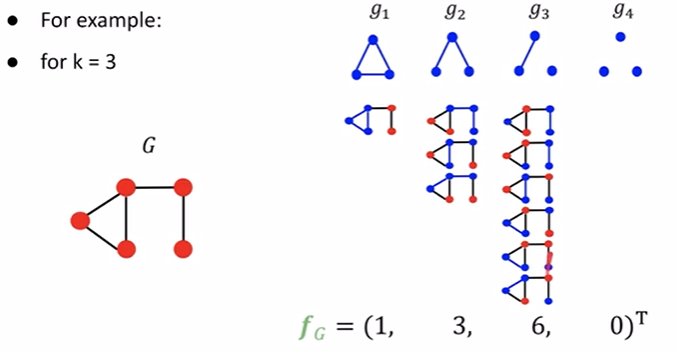
得到$f(G)$后对其作一个normalization
但是存在的问题是graphlet的计算十分复杂
weisfeiler-lehman kernel
- bag of colors
- capture graph structure within k-hop
- computationally efficient
- closely related to graph neural network
$$c^{(k+1)}(v) = HASH({ c^{(k)}(v), {c^{(k)}(u)}_{u \in N(v)} })$$
aggregate邻居的颜色,然后根据当前串hash table转到不同的color,相当于把邻居的颜色concat到自己的颜色后面。
color refinement结束之后,WL kernel计算每个颜色出现过的次数,用$\phi$转换成feature vector,最后将两个$\phi(G)$内积相乘,得到的结果越高说明similarity越高即颜色相同的node越多
这样的优点是它的开销相比graphlet的方式低了非常多。
color refinement也可以用来检测两个graph是否是isomorphism的