PAT甲级2023夏真题

算法树的遍历贪心 DFS 栈

字数统计: 2.3k阅读时长: 13 min

 2023/09/11 

PAT考试真题解析

[A-1] Trap (20)

DFS

题目

A robot is designed to move on a map from South toward North. When some obstacle is encountered, the robot can only turn toward West and moves until it can turn toward North and continue.

Given a squared map with $n×n$ blocks, a robot can start from any position below the bottom line (South) and its target is to reach the top line (North). (By the way, kindly remind you that the left-hand-side of the map is West and the right-hand-side is East.)

If some obstacles are placed in the map, the robot might get trapped if it starts from certain positions and can never reach the North line. For example, in the situation given by the following figure, the robot will be trapped if it starts from either position 7 or 8.

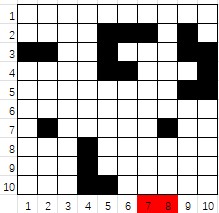
Your job is to point out those starting positions which will get the robot trapped.

Note: it is assumed that a robot can move out of the map boundary, and all the blocks around the map are open, without any obstacle. Hence if the robot starts from any position out of the West or East boundary, it can certainly reach North without any problem. Therefore we only have to consider the positions between the West and East boundaries (e.g. the positions from 1 to 10 below the South line in the above figure). Besides, as long as the robot can reach the North line, it is considered successful even of it ends up at out of the boundary (e.g. the robot will have to move out of the map if starts from either the positions 1 or 2, but it can still reach the North line).

Input Specification:

Each input file contains one test case. Each case starts from a positive integer $n (≤100)$ in a line, which is the size of the map. Then n lines follow, each contains n characters, which are either 0 for an open block, or 1 for a block with obstacle. The first line corresponds to the North boundary and the last line the South.

Output Specification:

Output in a line all the starting positions which can get the robot trapped, in increasing order. The positions are indexed from West to East, starting from 1. It is guaranteed that there is at least one output.
All the numbers must be separated by 1 space, and there must be no extra space at the beginning or the end of the line.

Sample Input:

Sample Output:

7 8

注意点与解析

这题可惜得我真的想四。题目的意思是从第n+1行出发，能往北走往北走，不能往北走就往西走，直到能往北走为止。而不是不能往北走后一直往西走。

代码

vector<vector<int>> num;

bool dfs(int i, int j) {
  if (i == 0 || j == 0) return true;
  if (num[i-1][j] == 0) return dfs(i - 1, j);
  else if (num[i][j-1] == 0)  return dfs(i, j - 1);
  else return false;
}

int main() {
  int n;
  cin >> n;
  num.resize(n + 1, vector<int>(n));
  for (int i = 0; i < n; i++)
    for (int j = 0; j < n; j++)
      scanf("%1d", &num[i][j]);
  vector<int> ans;
  for (int i = 0; i < n; i++) {
    bool flag = dfs(n, i);
    if (!flag)  ans.push_back(i + 1);
  }
  for (int i = 0; i < ans.size(); i++) {
    cout << ans[i];
    if (i != ans.size() - 1)  cout << " ";
  }
  return 0;
}

[A-2] Queue Using Two Stacks (25)

栈

题目

A queue (FIFO structure) can be implemented by two stacks (LIFO structure) in the following way:

Start from two empty stacks $s_1$ and $s_2$.
When element $e$ is enqueued, it is actually pushed onto $s_1$.
When we are supposed to dequeue, $s_2$ is checked first. If $s_2$ is empty everything in $s_1$ will be transferred to $s_2$ by popping from $s_1$ and immediately pushing onto $s_2$. Then we just pop from $s_2$ – the top element of $s_2$ must be the first one to enter $s_1$ thus is the first element that was enqueued.

Assume that each operation of push or pop takes 1 unit of time. You job is to tell the time taken for each dequeue.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer $N (≤10^3)$, which are the number of operations. Then $N$ lines follow, each gives an operation in the format

1	Operation Element

where Operation being I represents enqueue and O represents dequeue. For each I, Element is a positive integer that is no more than $10^6$. No Element is given for O operations.
It is guaranteed that there is at least one O operation.

Output Specification:

For each dequeue operation, print in a line the dequeued element and the unites of time taken to do this dequeue. The numbers in a line must be separated by 1 space, and there must be no extra space at the beginning or the end of the line.
In case that the queue is empty when dequeue is called, output in a line ERROR instead.

Sample Input:

10
I 20
I 32
O
I 11
O
O
O
I 100
I 66
O

Sample Output:

注意点与解析

没什么好说的，模拟就完事

代码

stack<int> s1, s2;

int main() {
  string s;
  int n, ele;
  cin >> n;
  for (int i = 0; i < n; i++) {
    cin >> s;
    if (s == "I") {
      cin >> ele;
      s1.push(ele);
    } else {
      int ans = 0;
      if (s2.empty()) {
        while (!s1.empty()) {
          int temp = s1.top();
          s1.pop();
          s2.push(temp);
          ans += 2;
        }
      }
      if (s2.empty()) {
        cout << "ERROR\n";
      } else {
        int temp = s2.top();
        s2.pop();
        ans++;
        printf("%d %d\n", temp, ans);
      }
    }
  }
  return 0;
}

[A-3] Rank of Binary Tree (25)

树的遍历

题目

Here we define the rank of a binary tree as $n_1×n_2/n_0$ where $n_i$ is the number of nodes of degree $i$ for $i=0,1,2$.
For example, given a tree shown by the figure, its rank is $2×3/4=1.5$.

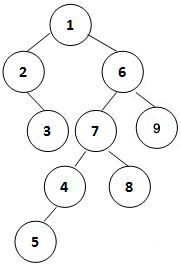
Given the inorder and preorder traversal sequences of a binary tree, you are supposed to calculate its rank.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer $N (≤20)$, which is the total number of nodes in the tree. Then given in the following 2 lines are the inorder and preorder traversal sequences of the tree, respectively. All the keys in the tree are distinct positive integers in the range of int.

Output Specification:

For each case, print in a line the way we calculate the rank, and the integer part of the rank. The format is:

1	n1 * n2 / n0 = rank

Sample Input:

1
2
3

9
2 3 1 5 4 7 8 6 9
1 2 3 6 7 4 5 8 9

Sample Output:

1	2 * 3 / 4 = 1

注意点与解析

老朋友了

代码

struct TreeNode {
  int val;
  TreeNode *left, *right;
};
vector<int> pre, in, ans(3);

TreeNode* insert(int preL, int preR, int inL, int inR) {
  if (preL > preR)  return NULL;
  TreeNode *root = new TreeNode;
  root -> val = pre[preL];
  root -> left = root -> right = NULL;
  int k = inL;
  while (k != inR && in[k] != pre[preL])  k++;
  int numLeft = k - inL;
  root -> left = insert(preL + 1, preL + numLeft, inL, k - 1);
  root -> right = insert(preL + numLeft + 1, preR, k + 1, inR);
  return root;
}

void dfs(TreeNode *root) {
  if (!root)  return;
  if (root -> left && root -> right)  ans[2]++;
  else if (root -> left || root -> right) ans[1]++;
  else  ans[0]++;
  dfs(root -> left);
  dfs(root -> right);
}

int main() {
  int n;
  cin >> n;
  pre.resize(n);
  in.resize(n);
  for (int i = 0; i < n; i++) cin >> in[i];
  for (int i = 0; i < n; i++) cin >> pre[i];
  TreeNode *root = insert(0, n - 1, 0, n - 1);
  dfs(root);
  printf("%d * %d / %d = %d", ans[1], ans[2], ans[0], ans[1]*ans[2]/ans[0]);
  return 0;
}

[A-4] Big Number (30)

DFS，贪心

题目

How to generate a big number of $N$ digits randomly? One way is to find $N$ kids, give each one a card with one’s index written on one side (hence it is assumed that the kids are indexed from 1 to $N$), and ask them to write down a 1-digit number randomly on the other side. Then let the kids pin their digits in a line, on the wall, one by one in ascending order of their indices.

However, it’s very difficult to let hundreds of thousands of kids to follow the order. The result is that we have cards pinned randomly all over the wall, some even show the wrong sides. For example, if the 23rd kid has written down 8, we are supposed to find the number 8 on the wall. But instead we might find 23… Your job is to rearrange these cards so that we can obtain the big number as required.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer $N (≤10^5)$. Then N lines follow, each describes a card in the format n1 n2 where the two numbers are the numbers written on the two sides of a card.

Output Specification:

For each test case, print in a line the N-digit number as required. That is, print the digits written by the kids in ascending order of their indices. In case that there are 1-digit numbers written on both sides, it would be hard to tell which one is the index and which one is the number written by the kid. Hence the solution may not be unique. In this case, just output the smallest resulting number.

It is guaranteed that a solution exists.

Sample Input:

Sample Output:

1	359114268072

注意点与解析

对于一组数，只要出现2位以上的数，它就必定表示这一组数的数位，那么另一个数就是这一位的数值。因此，出现不同情况的只可能是下标为1到9的9组数。
数据规模很小，所以算法的时间复杂度可以很奢侈。使用贪心，对每组的两个数哪个是下标哪个是数值，既然不知道，那就都试试。建立数组tv存这9组数，借助dfs从1到9逐渐完善tv。每试完一组，用集合cap来记住这一组的信息已经用掉了，把它erase掉，用完的信息存入tv，进入下一层dfs。

代码

int n;
void dfs(int cur, vector<int>& tv, vector<int>& res, set<pair<int,int>>& cap) {
  if (cur == 10 || cur > n) {
    res = min(res, tv);
    return;
  }
  for (int i = 0; i < 10; ++i) {
    if (cur==1&&i==0) continue;
    if (cap.count({cur, i})) {
      cap.erase({cur, i});
      tv[cur] = i;
      dfs(cur+1, tv, res, cap);
      cap.emplace(cur, i);
    }
    if (cap.count({i, cur})) {
      cap.erase({i, cur});
      tv[cur] = i;
      dfs(cur+1, tv, res, cap);
      cap.emplace(i, cur);
    }
  }
}
int main() {
  cin >> n;
  set<pair<int,int>> cap;
  vector<int> v(n+1);//storage: index >= 10
  for (int i = 0; i < n; ++i) {
    int a, b;
    cin >> a >> b;
    if (a >= 10) {
      v[a] = b;
    } else if (b >= 10) {
      v[b] = a;
    } else {
      if (cap.count({a, b})) cap.emplace(b, a);
      else cap.emplace(a, b);
    }
  }
  vector<int> res(10, 0x3f3f3f3f);
  vector<int> tv(10, 0x3f3f3f3f);//temp vector
  dfs(1, tv, res, cap);
  for (int i = 1; i < 10 && i <= n; ++i) {
    cout<<res[i];
  }
  for (int i = 10; i <= n; ++i) cout<<v[i];
  return 0;
}

Next Post

Tsunami：a learned multi-dimensional index for correlated data and skewed workloads
Previous Post

PAT甲级2018春真题