PAT甲级2017秋真题

算法链表哈希二叉搜索树数学模拟图论

字数统计: 1.9k阅读时长: 10 min

 2023/09/07 

PAT考试真题解析

[1132] Cut Integer (20)

数学模拟

题目

Cutting an integer means to cut a K digits lone integer Z into two integers of (K/2) digits long integers A and B. For example, after cutting Z = 167334, we have A = 167 and B = 334. It is interesting to see that Z can be devided by the product of A and B, as 167334 / (167 × 334) = 3. Given an integer Z, you are supposed to test if it is such an integer.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤ 20). Then N lines follow, each gives an integer Z (10 ≤ Z <$2^{31}$). It is guaranteed that the number of digits of Z is an even number.

Output Specification:

For each case, print a single line Yes if it is such a number, or No if not.

注意点与解析

直接⽤int保存num的值，计算出num的⻓度len，则令 d = pow(10, len / 2) 时，num取余d能得到后半部分的整数，num除以d能得到前半部分的整数，计算 num % (a * b) 是否等于0就可以得知是否可以被整除.
a * b 如果为0的时候不能取余，否则会浮点错误

代码

int main() {
  int n, num;
  cin >> n;
  while (n--) {
    cin >> num;
    string s = to_string(num);
    int len = s.length();
    int a = stoi(s.substr(0, len/2));
    int b = stoi(s.substr(len/2));
    if (a * b != 0 && num % (a * b) == 0)
      printf("Yes\n");
    else
      printf("No\n");
  }
  return 0;
}

[1133] Splitting A Linked List (25)

链表

题目

Given a singly linked list, you are supposed to rearrange its elements so that all the negative values appear before all of the non-negatives, and all the values in [0, K] appear before all those greater than K. The order of the elements inside each class must not be changed. For example, given the list being 18→7→-4→0→5→-6→10→11→-2 and K being 10, you must output -4→-6→-2→7→0→5→10→18→11.

Input Specification:

Each input file contains one test case. For each case, the first line contains the address of the first node, a positive $N (≤10^5)$ which is the total number of nodes, and a positive $K (≤10^3)$. The address of a node is a 5-digit nonnegative integer, and NULL is represented by −1.

Then $N$ lines follow, each describes a node in the format:

1	Address Data Next

where Address is the position of the node, Data is an integer in $[−10^5, 10^5]$, and Next is the position of the next node. It is guaranteed that the list is not empty.

Output Specification:

For each case, output in order (from beginning to the end of the list) the resulting linked list. Each node occupies a line, and is printed in the same format as in the input.

代码

const int maxn = 100005;
struct Node {
  int addr, data, next;
  int order;
};
vector<Node> node(maxn);

int main() {
  int begin, n, k, temp;
  cin >> begin >> n >> k;
  for (int i = 0; i < maxn; i++)
    node[i].order = maxn * 3;
  for (int i = 0; i < n; i++) {
    cin >> temp;
    cin >> node[temp].data >> node[temp].next;
    node[temp].addr = temp;
  }
  int negCnt = 0, lowerkCnt = 0, cnt = 0, total;
  for (int p = begin; p != -1; p = node[p].next) {
    if (node[p].data < 0) {
      node[p].order = negCnt++;
    } else if (node[p].data <= k) {
      node[p].order = maxn + lowerkCnt++;
    } else {
      node[p].order = maxn * 2 + cnt++;
    }
  }
  sort(node.begin(), node.end(), [&] (Node a, Node b) {
    return a.order < b.order;
  });
  total = negCnt + lowerkCnt + cnt;
  for (int i = 0; i < total; i++) {
    if (i != total - 1) {
      printf("%05d %d %05d\n", node[i].addr, node[i].data, node[i+1].addr);
    } else {
      printf("%05d %d -1", node[i].addr, node[i].data);
    }
  }
  return 0;
}

[1134] Vertex Cover (25)

图论、哈希

题目

A vertex cover of a graph is a set of vertices such that each edge of the graph is incident to at least one vertex of the set. Now given a graph with several vertex sets, you are supposed to tell if each of them is a vertex cover or not.

Input Specification:

Each input file contains one test case. For each case, the first line gives two positive integers $N$ and $M$ (both no more than $10^4$), being the total numbers of vertices and the edges, respectively. Then $M$ lines follow, each describes an edge by giving the indices (from 0 to $N−1$) of the two ends of the edge.

After the graph, a positive integer $K$ (≤ 100) is given, which is the number of queries. Then $K$ lines of queries follow, each in the format:

$N_v$ $v[1]$ $v[2]$ $⋯$ $v[N_v]$

where $N_v$ is the number of vertices in the set, and $v[i]$’s are the indices of the vertices.

Output Specification:

For each query, print in a line Yes if the set is a vertex cover, or No if not.

注意点与解析

每条边与顶点覆盖集合中的至少一个顶点”incident”是指顶点覆盖集合中的顶点与图中的边直接相连或具有直接的入边或出边关系。
顶点覆盖是指在一个无向图中选择一些顶点，使得图中的每条边至少有一个端点被选中。
⽤ vector v[n] 保存某结点属于的某条边的编号，⽐如a、b两个结点构成的这条边的编号为0，则 v[a].push_back(0)，v[b].push_back(0) ——表示a属于0号边，b也属于0号边。对于每⼀个集合做判断，遍历集合中的每⼀个元素，将当前元素能够属于的边的编号 i 对应的 hash[i] 标记为1，表示这条边是满⾜有⼀个结点出⾃集合S中的。最后判断 hash 数组中的每⼀个值是否都是1，如果有不是1的，说明这条边的两端结点没有⼀个出⾃集合S中.

代码

int main() {
  int n, m, a, b, k, num;
  cin >> n >> m;
  vector<int> v[n];
  for (int i = 0; i < m; i++) {
    cin >> a >> b;
    v[a].push_back(i);
    v[b].push_back(i);
  }
  cin >> k;
  for (int i = 0; i < k; i++) {
    cin >> num;
    int flag = 0;
    vector<int> hash1(m, 0);
    for (int j = 0; j < num; j++) {
      cin >> a;
      for (auto p: v[a])
        hash1[p] = 1;
    }
    for (auto p: hash1) {
      if (!p) {
        cout << "No" << endl;
        flag = 1;
        break;
      }
    }
    if (!flag)  cout << "Yes" << endl;
  }
  return 0;
}

[1135] Is It A Red-Black Tree (30)

二叉搜索树

题目

There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:

(1) Every node is either red or black.
(2) The root is black.
(3) Every leaf (NULL) is black.
(4) If a node is red, then both its children are black.
(5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.

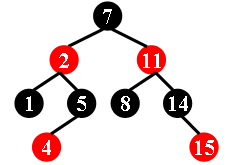
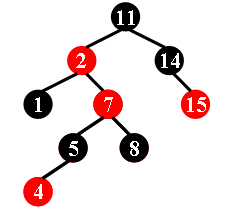
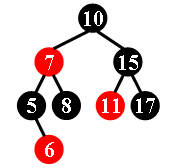
For each given binary search tree, you are supposed to tell if it is a legal red-black tree.

Input Specification:

Each input file contains several test cases. The first line gives a positive integer K (≤30) which is the total number of cases. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.

Output Specification:

For each test case, print in a line “Yes” if the given tree is a red-black tree, or “No” if not.

代码

struct TreeNode {
  int val;
  TreeNode *left, *right;
};
int pre, cur;

void create(TreeNode *&root, int x) {
  if (!root) {
    root = new TreeNode;
    root -> val = x;
    root -> left = root -> right = NULL;
    return;
  }
  if (abs(x) < abs(root -> val))  create(root -> left, x);
  else  create(root -> right, x);
}

void forLeaves(TreeNode *root, bool &flag) {
  if (!root || !flag) return;
  if (root -> val < 0) {
    if (root -> left) {
      if (root -> left -> val < 0) {
        flag = false;
        return;
      }
    }
    if (root -> right) {
      if (root -> right -> val < 0) {
        flag = false;
        return;
      }
    }
  }
  forLeaves(root -> left, flag);
  forLeaves(root -> right, flag);
}

void forBlackNum(TreeNode *root, bool &flag, int cur) {
  if (!flag)  return;
  if (!root) {
    if (pre == -1 || pre == cur) {
      pre = cur;
      return;
    } else {
      flag = false;
      return;
    }
  }
  int t = cur;
  if (root -> val > 0)  t++;
  forBlackNum(root -> left, flag, t);
  forBlackNum(root -> right, flag, t);
}

int main() {
  int k, num, temp;
  cin >> k;
  for (int i = 0; i < k; i++) {
    cin >> num;
    TreeNode *root = NULL;
    for (int j = 0; j < num; j++) {
      cin >> temp;
      create(root, temp);
    }
    pre = -1, cur = 0;
    bool flag = true;
    if (root -> val < 0)  flag = false;
    forLeaves(root, flag);
    forBlackNum(root, flag, 0);
    if (flag) cout << "Yes" << endl;
    else  cout << "No" << endl;
  }
  return 0;
}

Next Post

PAT甲级2017冬真题
Previous Post

PAT链表笔记