PAT甲级2017夏真题

算法树的遍历数学模拟 Set DFS

字数统计: 2.3k阅读时长: 13 min

 2023/09/03 

PAT考试真题解析

[1128] N Queens Puzzle (20)

数学模拟

题目

The “eight queens puzzle” is the problem of placing eight chess queens on an $8×8$ chessboard so that no two queens threaten each other. Thus, a solution requires that no two queens share the same row, column, or diagonal. The eight queens puzzle is an example of the more general $N$ queens problem of placing $N$ non-attacking queens on an $N×N$ chessboard. (From Wikipedia - “Eight queens puzzle”.)

Here you are NOT asked to solve the puzzles. Instead, you are supposed to judge whether or not a given configuration of the chessboard is a solution. To simplify the representation of a chessboard, let us assume that no two queens will be placed in the same column. Then a configuration can be represented by a simple integer sequence ($Q_1$ ,$Q_2$, ⋯, $Q_N$), where $Q_i$ is the row number of the queen in the i-th column. For example, Figure 1 can be represented by (4, 6, 8, 2, 7, 1, 3, 5) and it is indeed a solution to the 8 queens puzzle; while Figure 2 can be represented by (4, 6, 7, 2, 8, 1, 9, 5, 3) and is NOT a 9 queens’ solution.

Input Specification:

Each input file contains several test cases. The first line gives an integer $K (1<K≤200)$. Then $K$ lines follow, each gives a configuration in the format “$N$ $Q_1$ $Q_2$ … $Q_N$”, where $4≤N≤1000$ and it is guaranteed that $1≤Q_i≤N$ for all $i=1,⋯,N$. The numbers are separated by spaces.

Output Specification:

For each configuration, if it is a solution to the $N$ queens problem, print YES in a line; or NO if not.

注意点与解析

任意两个皇后都要不在同⼀⾏或者同⼀列，且不在斜对⻆线上

代码

int main() {
  int k, num;
  cin >> k;
  for (int i = 0; i < k; i++) {
    cin >> num;
    vector<int> v(num);
    bool result = true;
    for (int j = 0; j < num; j++) {
      cin >> v[j];
      for (int t = 0; t < j; t++) {
        if (v[j] == v[t] || abs(v[j]-v[t]) == abs(j-t)) {
          result = false;
          break;
        }
      }
    }
    cout << (result == true ? "YES\n" : "NO\n");
  }
  return 0;
}

[1129] Recommendation System (25)

Set

题目

Recommendation system predicts the preference that a user would give to an item. Now you are asked to program a very simple recommendation system that rates the user’s preference by the number of times that an item has been accessed by this user.

Input Specification:

Each input file contains one test case. For each test case, the first line contains two positive integers: N (≤ 50,000), the total number of queries, and K (≤ 10), the maximum number of recommendations the system must show to the user. Then given in the second line are the indices of items that the user is accessing – for the sake of simplicity, all the items are indexed from 1 to N. All the numbers in a line are separated by a space.

Output Specification:

For each case, process the queries one by one. Output the recommendations for each query in a line in the format:

1	query: rec[1] rec[2] ... rec[K]

where query is the item that the user is accessing, and rec[i] (i=1, … K) is the i-th item that the system recommends to the user. The first K items that have been accessed most frequently are supposed to be recommended in non-increasing order of their frequencies. If there is a tie, the items will be ordered by their indices in increasing order.

Note: there is no output for the first item since it is impossible to give any recommendation at the time. It is guaranteed to have the output for at least one query.

代码

struct Node {
  int value, cnt;
  friend bool operator < (const Node &a, const Node &b) {
    return (a.cnt != b.cnt)? a.cnt > b.cnt: a.value < b.value;
  }
};
int hash1[50001];
set<Node> s;

int main() {
  int n, k, num;
  cin >> n >> k;
  for (int i = 0; i < n; i++) {
    cin >> num;
    if (i) {
      printf("%d:", num);
      int count = 0;
      for (auto it = s.begin(); count < k && it != s.end(); it++) {
        printf(" %d", it -> value);
        count++;
      }
      cout << endl;
    }
    auto it = s.find(Node{num, hash1[num]});
    if (it != s.end())  s.erase(it);
    hash1[num]++;
    s.insert(Node{num, hash1[num]});
  }
  return 0;
}

[1130] Infix Expression (25)

树的遍历

题目

Given a syntax tree (binary), you are supposed to output the corresponding infix expression, with parentheses reflecting the precedences of the operators.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤ 20) which is the total number of nodes in the syntax tree. Then N lines follow, each gives the information of a node (the $i$-th line corresponds to the $i$-th node) in the format:

1	data left_child right_child

where data is a string of no more than 10 characters, left_child and right_child are the indices of this node’s left and right children, respectively. The nodes are indexed from 1 to N. The NULL link is represented by $−1$. The figures 1 and 2 correspond to the samples 1 and 2, respectively.

代码

struct Node {
  string data;
  int left, right;
};

vector<Node> nodes;
vector<bool> isRoot;

void inTraversal(int k, int root) {
  if (k == -1)  return;
  if ((nodes[k].left != -1 || nodes[k].right != -1) && k != root)
    cout << "(";
  inTraversal(nodes[k].left, root);
  cout << nodes[k].data;
  inTraversal(nodes[k].right, root);
  if ((nodes[k].left != -1 || nodes[k].right != -1) && k != root)
    cout << ")";
}

int main() {
  int n, a, b, i;
  cin >> n;
  nodes.resize(n + 1);
  isRoot.resize(n + 1, false);

  for (i = 1; i <= n; i++) {
    cin >> nodes[i].data >> nodes[i].left >> nodes[i].right;
    if (nodes[i].left != -1)  isRoot[nodes[i].left] = true;
    if (nodes[i].right != -1) isRoot[nodes[i].right] = true;
  }
  i = 1;
  while (isRoot[i]) i++;
  // printf("root is %d\n", i);
  inTraversal(i, i);
  cout << endl;
  return 0;
}

[1131] Subway Map (30)

DFS

题目

In the big cities, the subway systems always look so complex to the visitors. To give you some sense, the following figure shows the map of Beijing subway. Now you are supposed to help people with your computer skills! Given the starting position of your user, your task is to find the quickest way to his/her destination.

subway

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer $N (≤ 100)$, the number of subway lines. Then N lines follow, with the $i$-th $(i=1,⋯,N)$ line describes the $i$-th subway line in the format:

$M$ $S[1]$ $S[2]$ $…$ $S[M]$

where $M (≤ 100)$ is the number of stops, and S[$i$]’s $(i=1,⋯,M)$ are the indices of the stations (the indices are 4-digit numbers from 0000 to 9999) along the line. It is guaranteed that the stations are given in the correct order – that is, the train travels between $S[i]$ and $S[i+1]$ $(i=1,⋯,M−1)$ without any stop.

Note: It is possible to have loops, but not self-loop (no train starts from S and stops at S without passing through another station). Each station interval belongs to a unique subway line. Although the lines may cross each other at some stations (so called “transfer stations”), no station can be the conjunction of more than 5 lines.

After the description of the subway, another positive integer $K (≤ 10)$ is given. Then $K$ lines follow, each gives a query from your user: the two indices as the starting station and the destination, respectively.

The following figure shows the sample map.

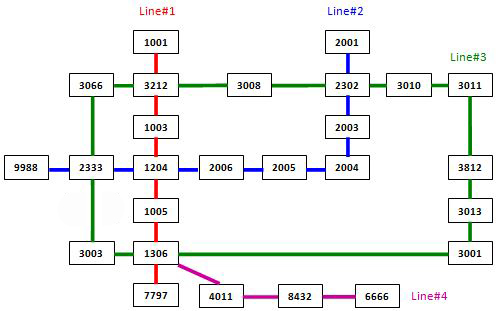
subway

Note: It is guaranteed that all the stations are reachable, and all the queries consist of legal station numbers.

Output Specification:

For each query, first print in a line the minimum number of stops. Then you are supposed to show the optimal path in a friendly format as the following:

1
2
3

Take Line#X1 from S1 to S2.
Take Line#X2 from S2 to S3.
......

where Xi’s are the line numbers and Si’s are the station indices. Note: Besides the starting and ending stations, only the transfer stations shall be printed.

If the quickest path is not unique, output the one with the minimum number of transfers, which is guaranteed to be unique.

注意点与解析

⼀遍DFS即可，DFS过程中要维护两个变量：minCnt-中途经停的最少的站; minTransfer-需要换乘的最⼩次数。
可以这样计算出⼀条线路的换乘次数：在 line[10000][10000] 的数组中保存每两个相邻站中间的线路是⼏号线。从头到尾遍历最终保存的路径，preLine 为前⼀⼩段的线路编号，如果当前的结点和前⼀个结点组成的这条路的线路编号和 preLine 不同，说明有⼀个换乘，就将 cnt+1，最后遍历完累加的 cnt 即是换乘的次数
- update：由于新的PAT系统中会显示原解法有⼀个测试⽤例内存超限，考虑到 line[10000][10000] 存储的⽅式太暴⼒了，所以将 line 换成了 unordered_map<int, int> line 存储的⽅式，第⼀个 int ⽤来存储线路，每次将前四位存储第⼀个线路，后四位存储第⼆个线路，使⽤ a[i-1]*10000+a[i] 的⽅式存储，第⼆个 int ⽤来保存两个相邻中间的线路是⼏号线
可以这样计算出⼀条线路中途停站的次数：在dfs的时候有个变量 cnt ，表示当前路线是所需乘的第⼏个站，每次dfs时候将 cnt+1 表示向下遍历⼀层，cnt 就是当前中途停站的次数
可以这样输出结果：和计算线路换乘次数的思路⼀样，每当 preLine 和当前 Line 值不同的时候就输出⼀句话，保存 preTransfer 表示上⼀个换乘站，最后不要忘记输出 preTransfer 和最后⼀个站之间的路即使最后⼀个站并不是换乘站

代码

const int maxn = 10000;
int vis[maxn], n, m, minStops, minTrans, st, ed;;
vector<vector<int>> v(maxn);
unordered_map<int, int> line;
vector<int> path, ans;

int transferCnt() {
  int cnt = -1, preLine = 0;
  for (int i = 1; i < path.size(); i++) {
    if (line[path[i-1] * maxn + path[i]] != preLine)
      cnt++;
    preLine = line[path[i-1] * maxn + path[i]];
  }
  return cnt;
}

void dfs(int now, int stops) {
  if (now == ed) {
    if (stops < minStops || (stops == minStops && transferCnt() < minTrans)) {
      minStops = stops;
      minTrans = transferCnt();
      ans = path;
    }
    return;
  }
  for (auto p: v[now]) {
    if (!vis[p]) {
      vis[p] = 1;
      path.push_back(p);
      dfs(p, stops + 1);
      path.pop_back();
      vis[p] = 0;
    }
  }
}

void printTool() {
  cout << minStops << endl;
  int preLine = 0, preTrans = st;
  for (int i = 1; i < ans.size(); i++) {
    if (line[ans[i-1] * maxn + ans[i]] != preLine) {
      if (preLine != 0)
        printf("Take Line#%d from %04d to %04d.\n", preLine, preTrans, ans[i-1]);
      preLine = line[ans[i-1] * maxn + ans[i]];
      preTrans = ans[i-1];
    }
  }
  printf("Take Line#%d from %04d to %04d.\n", preLine, preTrans, ed);
  return;
}

int main() {
  int k, pre, temp;
  cin >> n;
  for (int i = 0; i < n; i++) {
    cin >> m >> pre;
    for (int j = 1; j < m; j++) {
      cin >> temp;
      v[pre].push_back(temp);
      v[temp].push_back(pre);
      line[pre*maxn+temp] = line[temp*maxn+pre] = i + 1;
      pre = temp;
    }
  }
  cin >> k;
  for (int i = 0; i < k; i++) {
    cin >> st >> ed;
    minStops = maxn, minTrans = maxn;
    path.clear();
    path.push_back(st);
    vis[st] = 1;
    dfs(st, 0);
    vis[st] = 0;
    printTool();
  }
  return 0;
}

Next Post

PAT链表笔记
Previous Post

PAT算法杂烩笔记