PAT考试真题解析
[1172] Panda and PP Milk (20)
动态规划
题目

PP milk (盆盆奶)is Pandas’ favorite. They would line up to enjoy it as show in the picture. On the other hand, they could drink in peace only if they believe that the amount of PP milk is fairly distributed, that is, fatter panda can have more milk, and the ones with equal weight may have the same amount. Since they are lined up, each panda can only compare with its neighbor(s), and if it thinks this is unfair, the panda would fight with its neighbor.
Given that the minimum amount of milk a panda must drink is 200 ml. It is only when another bowl of milk is at least 100 ml more than its own that a panda can sense the difference.
Now given the weights of a line of pandas, your job is to help the breeder(饲养员)to decide the minimum total amount of milk that he/she must prepare, provided that the pandas are lined up in the given order.
Input Specification:
Each input file contains one test case. For each case, first a positive integer $n (≤10^4)$ is given as the number of pandas. Then in the next line, n positive integers are given as the weights (in kg) of the pandas, each no more than 200. the numbers are separated by spaces.
Output Specification:
For each test case, print in a line the minimum total amount of milk that the breeder must prepare, to make sure that all the pandas can drink in peace.
注意点与解析
- 扫两遍数组,第一遍从左往右分配,当前熊猫体重大于左边就+100,等于就分一样的奶,小于左边就只分配200,这样每个熊猫不会和左边的熊猫打架;第二遍从右往左分配,方法相同,这样每个熊猫不会和右边的熊猫打架。最后把两个数组合并,合并方式是取较大值。
- 这个问题可以归类为动态规划的原因是,它具备动态规划的两个关键要素:重叠子问题和最优子结构。
- 重叠子问题:在解决这个问题的过程中,我们可以观察到子问题的重复性。具体来说,对于每只熊猫,它能够获得的最大奶量取决于它左边和右边的熊猫的体重。因此,我们可以通过计算每只熊猫左边和右边的最大奶量,然后进行合并,得到当前熊猫的最大奶量。这样,我们可以将原始问题分解为更小的子问题,而这些子问题之间存在重叠。
- 最优子结构:问题的最优解可以通过子问题的最优解来构建。在这个问题中,每只熊猫能够获得的最大奶量只与它左边和右边的熊猫的最大奶量有关。因此,我们可以通过计算每只熊猫左边和右边的最大奶量,然后选择较大的值来构建当前熊猫的最大奶量。这样,我们可以通过子问题的最优解来推导出原始问题的最优解。
代码
1 |
|
[1173] How Many Ways to Buy a Piece of Land (25)
DFS+剪枝
题目
The land is for sale in CyberCity, and is divided into several pieces. Here it is assumed that each piece of land has exactly two neighboring pieces, except the first and the last that have only one. One can buy several contiguous(连续的) pieces at a time. Now given the list of prices of the land pieces, your job is to tell a customer in how many different ways that he/she can buy with a certain amount of money.
Input Specification:
Each input file contains one test case. Each case first gives in a line two positive integers: $N (≤10^4)$, the number of pieces of the land (hence the land pieces are numbered from 1 to N in order), and $M (≤10^9)$, the amount of money that your customer has.
Then in the next line, $N$ positive integers are given, where the i-th one is the price of the $i$-th piece of the land.
It is guaranteed that the total price of the land is no more than $10^9$.
Output Specification:
For each test case, print the number of different ways that your customer can buy. Notice that the pieces must be contiguous.
注意点与解析
- dp超内存…
- dfs+剪枝可以过,时间对比图放下面。
dfs+剪枝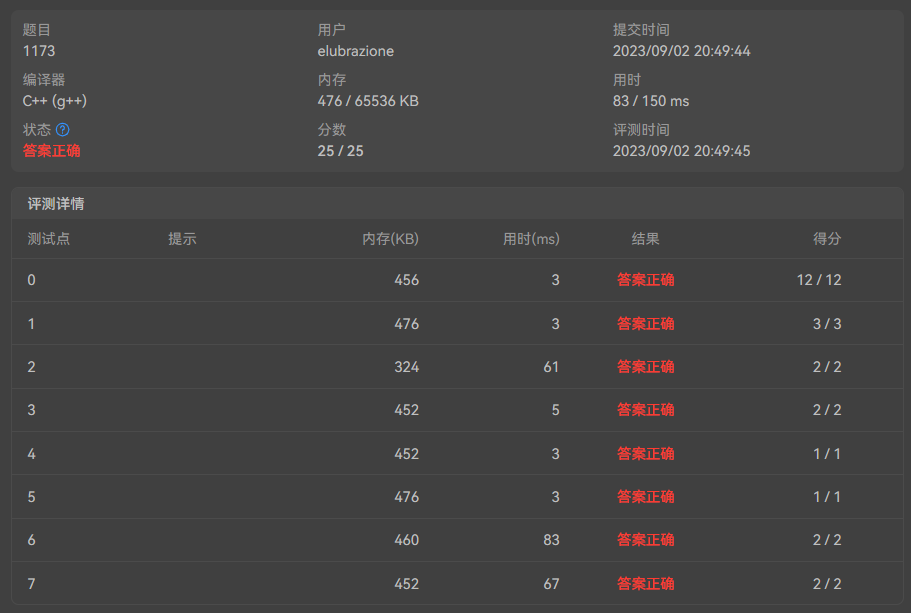
dp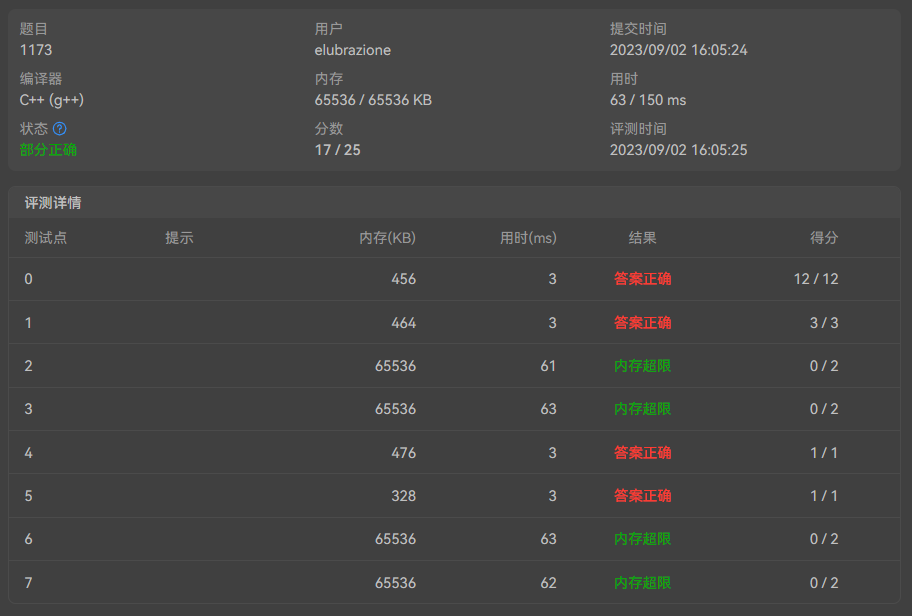
代码
DFS+剪枝
1 | vector<int> price; |
dp
1 | vector<int> price; |
[1174] Left-View of Binary Tree (25)
前序中序建树,输出每层第一个
题目
The left-view of a binary tree is a list of nodes obtained by looking at the tree from left hand side and from top down. For example, given a tree shown by the figure, its left-view is { 1, 2, 3, 4, 5 }

Given the inorder and preorder traversal sequences of a binary tree, you are supposed to output its left-view.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer $N (≤20)$, which is the total number of nodes in the tree. Then given in the following 2 lines are the inorder and preorder traversal sequences of the tree, respectively. All the keys in the tree are distinct positive integers in the range of int.
Output Specification:
For each case, print in a line the left-view of the tree. All the numbers in a line are separated by exactly 1 space, and there must be no extra space at the beginning or the end of the line.
代码
1 | struct TreeNode { |
[1175] Professional Ability Test (30)
拓扑排序、最短路径
题目
Professional Ability Test (PAT) consists of several series of subject tests. Each test is divided into several levels. Level A is a prerequisite (前置要求) of Level B if one must pass Level A with a score no less than $S$ in order to be qualified to take Level B. At the mean time, one who passes Level A with a score no less than $S$ will receive a voucher(代金券)of $D$ yuans (Chinese dollar) for taking Level B.
At the moment, this PAT is only in design and hence people would make up different plans. A plan is NOT consistent if there exists some test T so that T is a prerequisite of itself. Your job is to test each plan and tell if it is a consistent one, and at the mean time, find the easiest way (with minimum total $S$) to obtain the certificate of any subject test. If the easiest way is not unique, find the one that one can win the maximum total value of vouchers.
Input Specification:
Each input file contains one test case. For each case, the first line gives two positive integers $N (≤1000)$ and $M$, being the total numbers of tests and prerequisite relations, respectively. Then M lines follow, each describes a prerequisite relation in the following format:
1 | T1 T2 S D |
where T1 and T2 are the indices (from 0 to $N−1$) of the two distinct tests; S is the minimum score (in the range (0, 100]) required to pass T1 in order to be qualified to take T2; and D is the value of the voucher (in the range (0, 500]) one can receive if one passes T1 with a score no less than S and plan to take T2. It is guaranteed that at most one pair of S and D are defined for a prerequisite relation.
Then another positive integer $K (≤N)$ is given, followed by $K$ queries of tests. All the numbers in a line are separated by spaces.
Output Specification:
Print in the first line Okay. if the whole plan is consistent, or Impossible. if not.
If the plan is consistent, for each query of test T, print in a line the easiest way to obtain the certificate of this test, in the format:
1 | T0->T1->...->T |
However, if T is the first level of some subject test (with no prerequisite), print You may take test T directly. instead.
If the plan is impossible, for each query of test T, check if one can take it directly or not. If the answer is yes, print in a line You may take test T directly.; or print Error. instead.
注意点与解析
- 先判断是否DAG,再求路径。DAG的判断算法笔记上已经有模板,照抄即可;
- 而对于求路径,由于起点可能有多个而终点只有一个,如果正向求解,需要遍历每个入度为0的点,容易导致测试点7超时。因此可以采用两种变通的方法:
- 倒过来,从唯一的终点出发往回DFS,那么就要建立逆邻接表;
- 新建一个顶点作为所有起点的源点,一遍迪杰斯特拉算法即可。新建一个顶点下标选择为n,在新建的n结点和原始入度为0的结点也就是没有前提比赛的结点之间加入一条有向边(注意这个时候已经判断完是否是DAG图了,可以将前面找到最初的入度为0的结果保存到一个set里面,放到set里面是为了后续输出路径判断有无前置比赛时使用
count()查询统计),vouch和score都设置为0,将这个点作为起点使用Dijkstra得到到其它各个结点的最短路径,并记录前驱结点,最后使用dfs得到路径(注意dfs的方法和语句顺序)。
代码
1 | struct Node { |