PAT甲级2020春真题

算法素数哈希图模拟快乐模拟

字数统计: 3.1k阅读时长: 16 min

 2023/08/31 

PAT考试真题解析

[1168] Prime Day (20)

素数

题目

1168

The above picture is from Sina Weibo, showing May 23rd, 2019 as a very cool “Prime Day”. That is, not only that the corresponding number of the date 20190523 is a prime, but all its sub-strings ended at the last digit 3 are prime numbers.

Now your job is to tell if a given date is a Prime Day.

Input Specification:

Each input file contains one test case. For each case, a date between January 1st, 0001 and December 31st, 9999 is given, in the format yyyymmdd.

Output Specification:

For each given date, output in the decreasing order of the length of the substrings, each occupies a line. In each line, print the string first, followed by a space, then Yes if it is a prime number, or No if not. If this date is a Prime Day, print in the last line All Prime!.

注意点与解析

这道题用筛法会超时，其实题目没有说要求所有素数这样关键词地时候直接用根号法就行了.
注意 string 类型用printf() 输出时要用 c_str().

代码

bool isPrime(int number) {
  if (number <= 1) return false;
  int sqr = (int)sqrt(number), i;
  for (i = 2; i <= sqr; i++)
    if (number % i == 0) return false;
  return true;
}

int main() {
  bool flag = true;
  string n;
  cin >> n;
  for (int i = 8; i > 0; i--) {
    string str = n.substr(8 - i, i);
    int cur = stoi(str);
    bool fg = isPrime(cur);
    printf("%s %s\n", str.c_str(), fg? "Yes": "No");
    if (!fg) flag = false;
  }
  if (flag) cout << "All Prime!";
  return 0;
}

[1169] The Judger (25)

哈希

题目

A game of numbers has the following rules: at the beginning, two distinct positive integers are given by the judge. Then each player in turn must give a number to the judge. The number must be the difference of two numbers that are previously given, and must not be duplicated to any of the existed numbers. The game will run for several rounds. The one who gives a duplicate number or even a wrong number will be kicked out.

Your job is to write a judger program to judge the players’ numbers and to determine the final winners.

Input Specification:

Each input file contains one test case. For each case, the first line gives two distinct positive integers to begin with. Both numbers are in $[1,10^5]$.

In the second line, two numbers are given: $N (2≤N≤10)$, the number of players, and $M (2≤M≤10^3)$, the number of rounds.

Then $N$ lines follow, each contains $M$ positive integers. The i-th line corresponds to the i-th player $(i=1,⋯,N)$. The game is to start from the 1st player giving his/her 1st number, followed by everybody else giving their 1st numbers in the 1st round; then everyone give their 2nd numbers in the 2nd round, and so on so forth.

Output Specification:

If the i-th player is kicked out in the k-th round, print in a line Round #k: i is out.. The rest of the numbers given by the one who is out of the game will be ignored. If more than one player is out in the same round, print them in increasing order of their indices. When the game is over, print in the last line Winner(s): W1 W2 ... Wn, where W1 ... Wn are the indices of the winners in increasing order. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the beginning or the end of the line. If there is no winner, print No winner. instead.

注意点与解析

这题真的是非常离谱…这个题目得看懂，The number must be the difference of two numbers that are previously given, and must not be duplicated to any of the existed numbers. 首先是每个选手给出的数得属于之前给出的所有的数（包括开局裁判给的那两个数）的差的集合；其次不能重复，如果重复也出局。这个 difference 代表两个数的差，一开始可能没反应过来，不过分析测试样例之后应该能明白过来；
做的时候思路是对的，用两个哈希，一个用来放当前合理的差值，一个标记这个数字是否出现过，但是出现了两个问题：
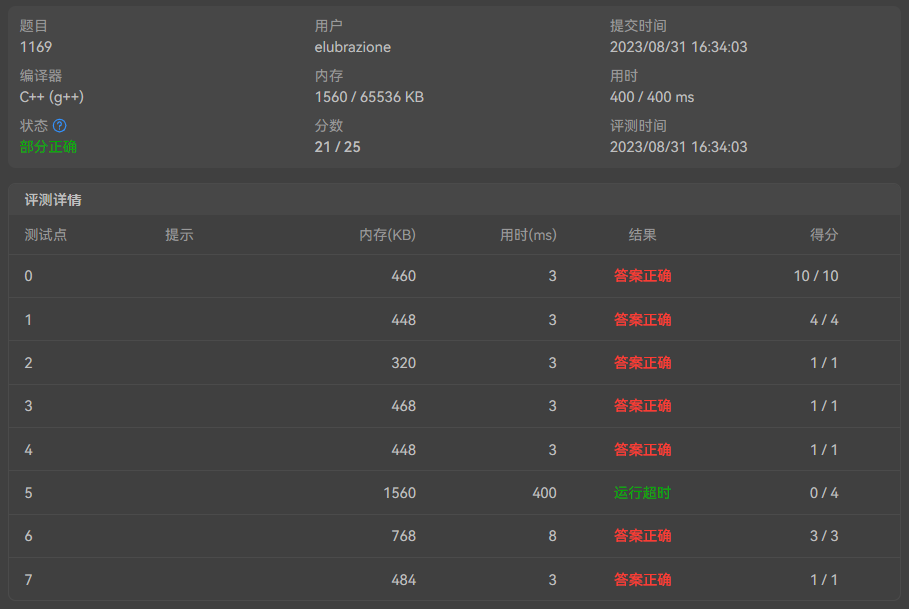
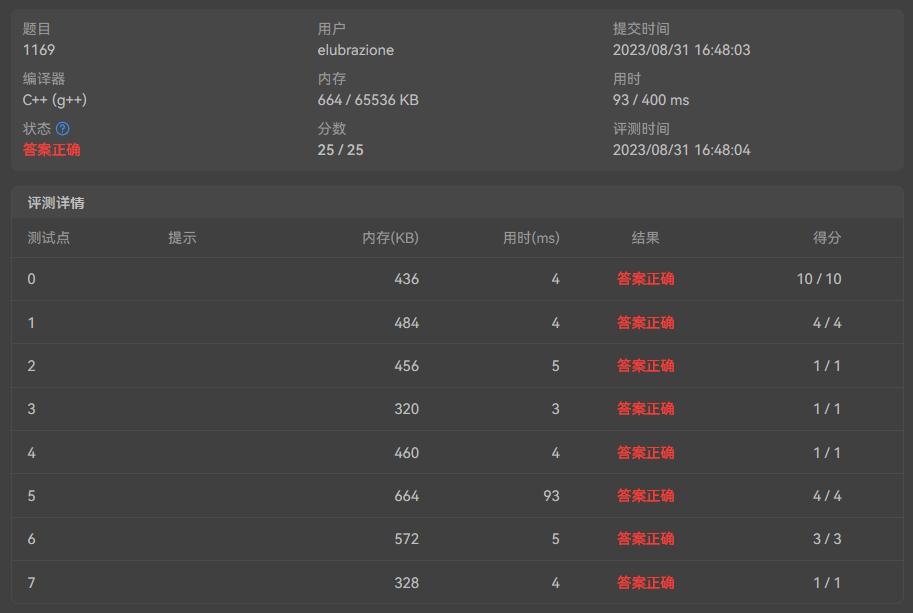
- 测试点3和4一直过不去，这个问题我一直没解决，后来上网搜发现是初始化的时候得记得标记初始给的那两个数为出现过。确实，must not be duplicated to any of the existed numbers 当然也包括裁判给的那两个数。
- 有一个测试点超时…后来发现是 千万不能用 STL 的 MAP…. ，直接int数组开个100001的空间不香吗，不香吗…我的沉默震耳欲聋…顺便一说这题 unordered_map也是超时。所以我学到的教训是能用数组用数组，反正功能是一样的。下面放个对比图。

代码

vector<bool> winner;
vector<vector<int>> info;
set<int> w;
vector<int> pool;
bool mp[100001], mp2[100001];

int main() {
  int n, m, a, b, cur;
  cin >> a >> b;
  pool.push_back(a);
  pool.push_back(b);
  mp[abs(a-b)] = true;
  mp2[a] = mp2[b] = true;

  cin >> n >> m;
  winner.resize(n, true);
  info.resize(m, vector<int>(n));

  for (int i = 0; i < n; i++)
    for (int j = 0; j < m; j++)
      scanf("%d", &info[j][i]);

  for (int i = 0; i < m; i++) {
    for (int j = 0; j < n; j++) {
      if (!winner[j]) continue;
      if (mp[info[i][j]] && !mp2[info[i][j]]) {
        for (auto p: pool)
          mp[abs(p-info[i][j])] = true;
        pool.push_back(info[i][j]);
        mp2[info[i][j]] = true;
      } else {
        printf("Round #%d: %d is out.\n", i + 1, j + 1);
        winner[j] = false;
      }
    }
  }

  for (int i = 0; i < n; i++)
    if (winner[i])  w.insert(i + 1);
  if (!w.size()) cout << "No winner.";
  else {
    printf("Winner(s):");
    for (auto p: w) printf(" %d", p);
  }
  return 0;
}

[1170] Safari Park (25)

图模拟

题目

A safari park（野生动物园）has $K$ species of animals, and is divided into $N$ regions. The managers hope to spread the animals to all the regions, but not the same animals in the two neighboring regions. Of course, they also realize that this is an NP complete problem, you are not expected to solve it. Instead, they have designed several distribution plans. Your job is to write a program to help them tell if a plan is feasible.

Input Specification:

Each input file contains one test case. For each case, the first line gives 3 integers: $N (0<N≤500)$, the number of regions; $R (≥0)$, the number of neighboring relations, and $K (0<K≤N)$, the number of species of animals. The regions and the species are both indexed from 1 to $N$.

Then $R$ lines follow, each gives the indices of a pair of neighboring regions, separated by a space.

Finally there is a positive $M (≤20)$ followed by M lines of distribution plans. Each plan gives $N$ indices of species in a line (the $i$-th index is the animal in the $i$-th rigion), separated by spaces. It is guaranteed that any pair of neighboring regions must be different, and there is no duplicated neighboring relations.

Output Specification:

For each plan, print in a line Yes if no animals in the two neighboring regions are the same, or No otherwise. However, if the number of species given in a plan is not $K$, you must print Error: Too many species. or Error: Too few species. according to the case.

注意点与解析

怎么说呢，我以为会超时但是其实并没有系列，暴力万岁。

代码

int n, r, k, m;
set<int> s;
vector<int> region;
vector<vector<int>> G;

bool judge() {
  for (int i = 1; i <= n; i++)
    for (auto p: G[i])
      if (region[p] == region[i])
        return false;
  return true;
}

int main() {
  cin >> n >> r >> k;
  G.resize(n + 1);
  region.resize(n + 1, 0);
  int a, b;
  for (int i = 0; i < r; i++) {
    cin >> a >> b;
    G[a].push_back(b);
    G[b].push_back(a);
  }
  cin >> m;
  for (int i = 0; i < m; i++) {
    s.clear();
    for (int j = 1; j <= n; j++) {
      cin >> region[j];
      s.insert(region[j]);
    }
    if (s.size() != k) {
      if (s.size() > k) printf("Error: Too many species.\n");
      else  printf("Error: Too few species.\n");
      continue;
    }
    bool flag = judge();
    printf("%s\n", flag? "Yes": "No");
  }
  return 0;
}

[1171] Replacement Selection (30)

快乐模拟

题目

When the input is much too large to fit into memory, we have to do external sorting instead of internal sorting. One of the key steps in external sorting is to generate sets of sorted records (also called runs) with limited internal memory. The simplest method is to read as many records as possible into the memory, and sort them internally, then write the resulting run back to some tape. The size of each run is the same as the capacity of the internal memory.

Replacement Selection sorting algorithm was described in 1965 by Donald Knuth. Notice that as soon as the first record is written to an output tape, the memory it used becomes available for another record. Assume that we are sorting in ascending order, if the next record is not smaller than the record we have just output, then it can be included in the run.

For example, suppose that we have a set of input { 81, 94, 11, 96, 12, 99, 35 }, and our memory can sort 3 records only. By the simplest method we will obtain three runs: { 11, 81, 94 }, { 12, 96, 99 } and { 35 }. According to the replacement selection algorithm, we would read and sort the first 3 records { 81, 94, 11 } and output 11 as the smallest one. Then one space is available so 96 is read in and will join the first run since it is larger than 11. Now we have { 81, 94, 96 }. After 81 is out, 12 comes in but it must belong to the next run since it is smaller than 81. Hence we have { 94, 96, 12 } where 12 will stay since it belongs to the next run. When 94 is out and 99 is in, since 99 is larger than 94, it must belong to the first run. Eventually we will obtain two runs: the first one contains { 11, 81, 94, 96, 99 } and the second one contains { 12, 35 }.

Your job is to implement this replacement selection algorithm.

Input Specification:

Each input file contains several test cases. The first line gives two positive integers $N (≤10^5)$ and $M (<N/2)$, which are the total number of records to be sorted, and the capacity of the internal memory. Then N numbers are given in the next line, all in the range of int. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print in each line a run (in ascending order) generated by the replacement selection algorithm. All the numbers in a line must be separated by exactly 1 space, and there must be no extra space at the beginning or the end of the line.

注意点与解析

什么题目这么长…暴力模拟之后后面的测试点美美超时，看了一下网上的说法是有个快乐模拟，先留个暴力的结果图，明天早上看看算法笔记的十三章（~~2023.08.31 22:20~~）
看了，思路就是暴力模拟那样，只不过要想想怎么优化，只不过要用优先队列来处理排序部分。由于内存中需要对M个数排序，并且移除最小的数，用低优先级先出的优先队列最合适。但是内存中有些数会长期滞留，而优先队列只能让最小的数出队，不能让次小或更大的数出队。为此使用一个remain数组，滞留的数全部放在这里。刚开始先把优先队列填满，然后在循环中每次输出一个数，再读入一个数：读入的数如果比上次输出的数小，表明会长期滞留，就进remain，否则进优先队列。如果要输出的时候优先队列为空，表示内存中全部是滞留的数，结束当前初始归并段，把remain的数全部加入优先队列，产生新的归并段。
while循环的条件是 cnt < n，如果把cnt自增放在将元素出队的时候，最后一行会没法输出，所以把计数器的更改放到打印完之后。
注意低级优先队列的定义方法：priority_queue<int, vector<int>, greater<int>> now，int、double以及char型默认数字大或者字典序大的元素优先级高，也就是 less<int>. 这里 greater<int> 代表的是重载小于号 < 时，return a > b，也就是数字大的优先级小（小于号），即数字小的优先级大。简单记忆的话就是优先队列排序规则和数组排序规则相反。

结构体大小比较定义

代码

暴力模拟

vector<int> now;
vector<int> num, k(1e5 + 1, INT_MIN);
vector<vector<int>> ans(1);

int main() {
  int n, m, mx = INT_MIN;
  cin >> n >> m;
  num.resize(n);
  for (int i = 0; i < n; i++) {
    cin >> num[i];
    mx = max(mx, num[i]);
  }

  int i = 0, cur = 0;
  while (i < n + m) {
    if (now.size() < m && i < n) {
      now.push_back(num[i++]);
      continue;
    }
    sort(now.begin(), now.end());
    int p = 0;
    while (p < now.size() && now[p] <= k[cur])  p++;
    if (p == now.size()) {
      ans.push_back(vector<int>());
      cur++;
      p = 0;
    }
    ans[cur].push_back(now[p]);
    k[cur] = now[p];
    if (i < n) now[p] = num[i];
    else  now.erase(now.begin() + p);
    i++;
  }
  for (int i = 0; i < ans.size(); i++) {
    for (int j = 0; j < ans[i].size(); j++) {
      if (j) cout << " ";
      cout << ans[i][j];
    }
    cout << endl;
  }
  return 0;
}

低级优先队列

vector<int> num, remain, ans;
priority_queue<int, vector<int>, greater<int>> now;

int main() {
  int n, m, cnt = 0, i, pre = INT_MIN;
  cin >> n >> m;
  num.resize(n);
  for (i = 0; i < n; i++) cin >> num[i];
  i = 0;
  while (now.size() < m)  now.push(num[i++]);
  while (cnt < n) {
    if (now.empty()) {
      for (auto item: remain)
        now.push(item);
      for (int j = 0; j < ans.size(); j++) {
        cout << ans[j];
        if (j != ans.size() - 1)  cout << " ";
      }
      cnt += ans.size();
      cout << endl;
      ans.clear();
      remain.clear();
    } else {
      int cur = now.top();
      now.pop();
      ans.push_back(cur);
      pre = cur;
      if (i < n) {
        if (num[i] <= pre)
          remain.push_back(num[i++]);
        else  now.push(num[i++]);
      }
    }
  }
  return 0;
}

Next Post

PAT甲级2020秋真题
Previous Post

PAT甲级2017春真题