PAT甲级2017春真题

算法树的遍历数学模拟贪心图论

字数统计: 2.1k阅读时长: 11 min

 2023/08/31 

PAT考试真题解析

[1124] Raffle for Weibo Followers (20)

模拟题

题目

John got a full mark on PAT. He was so happy that he decided to hold a raffle（抽奖） for his followers on Weibo – that is, he would select winners from every N followers who forwarded his post, and give away gifts. Now you are supposed to help him generate the list of winners.

Input Specification:

Each input file contains one test case. For each case, the first line gives three positive integers $M (≤ 1000)$, $N$ and $S$, being the total number of forwards, the skip number of winners, and the index of the first winner (the indices start from 1). Then M lines follow, each gives the nickname (a nonempty string of no more than 20 characters, with no white space or return) of a follower who has forwarded John’s post.

Note: it is possible that someone would forward more than once, but no one can win more than once. Hence if the current candidate of a winner has won before, we must skip him/her and consider the next one.

Output Specification:

For each case, print the list of winners in the same order as in the input, each nickname occupies a line. If there is no winner yet, print Keep going... instead.

代码

vector<string> post;
map<string, bool> mp;

int main() {
  int m, n, s, i = 0, cnt = 0;
  cin >> m >> n >> s;
  string str;
  post.resize(m + 1);
  for (i = 1; i <= m; i++)  cin >> post[i];
  i = s;
  while (i <= m) {
    if (mp.find(post[i]) == mp.end()) {
      cout << post[i] << endl;
      mp[post[i]] = true;
      cnt++;
      i += n;
    } else {
      i++;
    }
  }
  if (!cnt) cout << "Keep going...";
  return 0;
}

[1125] Chain the Ropes (25)

排序、贪心

题目

Given some segments of rope, you are supposed to chain them into one rope. Each time you may only fold two segments into loops and chain them into one piece, as shown by the figure. The resulting chain will be treated as another segment of rope and can be folded again. After each chaining, the lengths of the original two segments will be halved.

1125

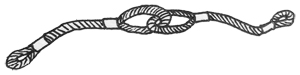
Your job is to make the longest possible rope out of N given segments.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer $N (2≤N≤10^4)$. Then $N$ positive integer lengths of the segments are given in the next line, separated by spaces. All the integers are no more than $10^4$.

Output Specification:

For each case, print in a line the length of the longest possible rope that can be made by the given segments. The result must be rounded to the nearest integer that is no greater than the maximum length.

注意点与解析

这题的关键点是看懂这句话：The resulting chain will be treated as another segment of rope and can be folded again. 也就是两根绳子合并成一根新的绳子，之后再用于合并其它绳子。根据后面说的 After each chaining, the lengths of the original two segments will be halved 每次合并会让两根绳子的长度都减至一半。
那么我们直观地可以想到，先合并的绳子被合并的次数就越多，损失就越多，所以要先合并短的绳子，排序完模拟合并就行。

代码

vector<double> ropes;

int main() {
  int n;
  cin >> n;
  ropes.resize(n);
  for (int i = 0; i < n; i++)
    cin >> ropes[i];
  sort(ropes.begin(), ropes.end());
  double cur = ropes[0];
  for (int i = 1; i < n; i++) {
    cur = (cur + ropes[i]) / 2;
  }
  cout << (int)cur;
  return 0;
}

[1126] Eulerian Path (25)

图论

题目

In graph theory, an Eulerian path is a path in a graph which visits every edge exactly once. Similarly, an Eulerian circuit is an Eulerian path which starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of Konigsberg problem in 1736. It has been proven that connected graphs with all vertices of even degree have an Eulerian circuit, and such graphs are called Eulerian. If there are exactly two vertices of odd degree, all Eulerian paths start at one of them and end at the other. A graph that has an Eulerian path but not an Eulerian circuit is called semi-Eulerian.

Given an undirected graph, you are supposed to tell if it is Eulerian, semi-Eulerian, or non-Eulerian.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 2 numbers N (≤ 500), and M, which are the total number of vertices, and the number of edges, respectively. Then M lines follow, each describes an edge by giving the two ends of the edge (the vertices are numbered from 1 to N).

Output Specification:

For each test case, first print in a line the degrees of the vertices in ascending order of their indices. Then in the next line print your conclusion about the graph – either Eulerian, Semi-Eulerian, or Non-Eulerian. Note that all the numbers in the first line must be separated by exactly 1 space, and there must be no extra space at the beginning or the end of the line.

注意点与解析

分析题目，an Eulerian path is a path in a graph which visits every edge exactly once 这句话没什么用，不要纠结于这句话说的所谓一次遍历所有的边不走回头路，后面的方法提供了简单的判断方法。
判断方法：
- It has been proven that connected graphs with all vertices of even degree have an Eulerian circuit, and such graphs are called Eulerian. 这句话告诉我们两个信息，所有的结点的度数皆为偶数的是Eulerian，当然前提是这个图是个连通图；
- If there are exactly two vertices of odd degree, all Eulerian paths start at one of them and end at the other. 如果除了有两个结点度数是奇数，剩下的是偶数，那么具有欧拉路径，这里欧拉路径的头尾是这两个具有奇数度的结点，当然前提还是这个图是连通图。
总结：
- 是连通图：
  - 所有度数为偶数 => Eulerian
  - 除了两个奇数度结点剩下都是偶数 => 有欧拉路径 => Semi-Eulerian
  - 都不是 => Non-Eulerian
- 不是连通图 => Non-Eulerian
这道题主要是要认真看题目。
然后说一下判断连通图的方法，可以使用求连通分量的方法（下列代码），也可以只一次dfs，把cnt变量放到dfs内部，求dfs调用的次数（即访问的结点的个数），最后判断cnt是否等于所有结点个数。

代码

vector<int> degree;
vector<bool> vis;
vector<vector<int>> G;

void dfs(int u, int n) {
  vis[u] = true;
  for (int i = 1; i <= n; i++) {
    if (G[u][i] == 1 && vis[i] == false)
      dfs(i, n);
  }
}

int printDegree(int n) {
  int num = degree[1]%2? 0: 1;
  cout << degree[1];
  for (int i = 2; i <= n; i++) {
    cout << " " << degree[i];
    if (!(degree[i] % 2))  num++;
  }
  cout << endl;
  if (num == n)  return 2;
  else if (num + 2 == n)  return 1;
  else  return 0;
}

int main() {
  int n, m, a, b, cnt = 0;
  cin >> n >> m;
  vis.resize(n + 1, false);
  degree.resize(n + 1);
  G.resize(n + 1, vector<int>(n + 1));
  for (int i = 0; i < m; i++) {
    cin >> a >> b;
    G[a][b] = 1;
    G[b][a] = 1;
    degree[a]++;
    degree[b]++;
  }
  int isEulerian = printDegree(n);
  for (int i = 1; i <= n; i++)
    if (vis[i] == false) {
      dfs(i, n);
      cnt++;
    }
  if (cnt == 1) {
    if (isEulerian == 2)  cout << "Eulerian";
    else if (isEulerian == 1)  cout << "Semi-Eulerian";
    else  cout << "Non-Eulerian";
  } else {
    cout << "Non-Eulerian";
  }
  return 0;
}

[1127] ZigZagging on a Tree (30)

中序后序转层序，锯齿状输出

题目

Suppose that all the keys in a binary tree are distinct positive integers. A unique binary tree can be determined by a given pair of postorder and inorder traversal sequences. And it is a simple standard routine to print the numbers in level-order. However, if you think the problem is too simple, then you are too naive. This time you are supposed to print the numbers in “zigzagging order” – that is, starting from the root, print the numbers level-by-level, alternating between left to right and right to left. For example, for the following tree you must output: 1 11 5 8 17 12 20 15.

1127

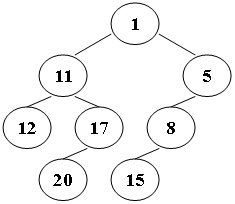
Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the inorder sequence and the third line gives the postorder sequence. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the zigzagging sequence of the tree in a line. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the end of the line.

注意点与解析

用 q.size() 统计个数，有规划固定个数地pop出来，将当前队列里的元素收集起来放在数组里。再根据层数判断是否要反转数组。

代码

struct TreeNode {
  int val;
  TreeNode *left, *right;
};
vector<int> in, post;

TreeNode* insert(int inL, int inR, int postL, int postR) {
  if (inL > inR)  return NULL;
  TreeNode *root = new TreeNode;
  root -> val = post[postR];
  root -> left = root -> right = NULL;

  int k = inL;
  while (k <= inR && in[k] != post[postR])  k++;
  int numLeft = k - inL;
  root -> left = insert(inL, k - 1, postL, postL + numLeft - 1);
  root -> right = insert(k + 1, inR, postL + numLeft, postR - 1);
  return root;
}

int cnt = 1;
void levelTraversal(TreeNode *root, int n) {
  queue<TreeNode*> q;
  q.push(root);
  vector<int> vec;
  int ctrl = 1;
  while (!q.empty()) {
    int num = q.size();
    while (num--) {
      auto node =  q.front();
      q.pop();
      vec.push_back(node -> val);
      if (node -> left) q.push(node -> left);
      if (node -> right)  q.push(node -> right);
    }
    if (ctrl%2) reverse(vec.begin(), vec.end());
    for (auto p: vec) {
      cout << p;
      if (cnt != n) cout << " ";
      cnt++;
    }
    ctrl++;
    vec.clear();
  }
}

int main() {
  int n;
  cin >> n;
  in.resize(n);
  post.resize(n);
  for (int i = 0; i < n; i++) cin >> in[i];
  for (int i = 0; i < n; i++) cin >> post[i];
  TreeNode *root = insert(0, n - 1, 0, n - 1);
  levelTraversal(root, n);
  return 0;
}

Next Post

PAT甲级2020春真题
Previous Post

Learning Multi-dimensional Indexes