本文的重点是减少不必要的扫描和过滤开销,以牺牲写入为代价,针对读取(查询速度)进行了优化。
Flood, a multi-dimensional in-memory read-optimized index that automatically adapts itself to a particular dataset and workload by jointly optimizing the index structure and data storage layout. It achieves up to three orders of magnitude faster performance for range scanswith predicates than state-of-theart multi-dimensional indexes or sort orders on real-world datasets and workloads.
问题
- 当必须在多个属性列上过滤数据时,辅助索引庞大的存储开销和跟踪指针产生的延迟让其只适用于索引属性上的谓词具有非常高的选择性的场景;
- 多维索引are extremely hard to tune(sort hierarchically on multiple attributes requires an admin to carefully pick the sort order. The admin must therefore know which columns are accessed together, and their selectivity, to make an informed decision)
- there is no single approach (even if tuned correctly) that dominates all others. The performance of state-of-art model depends on the data distribution and queryworkload
- most existing techniques cannot be fully tailored for a specific data distribution and query workload.
Overview
two keys
- Flood先使用一个简单负载来学习负载特性,基于这些信息得到训练参数;
- 使用经验CDF模型将多维和潜在偏斜的数据分布投影到更均匀的空间中。这个“平坦化”步骤有助于限制搜索的点的数量,是实现良好性能的关键。
Architecture
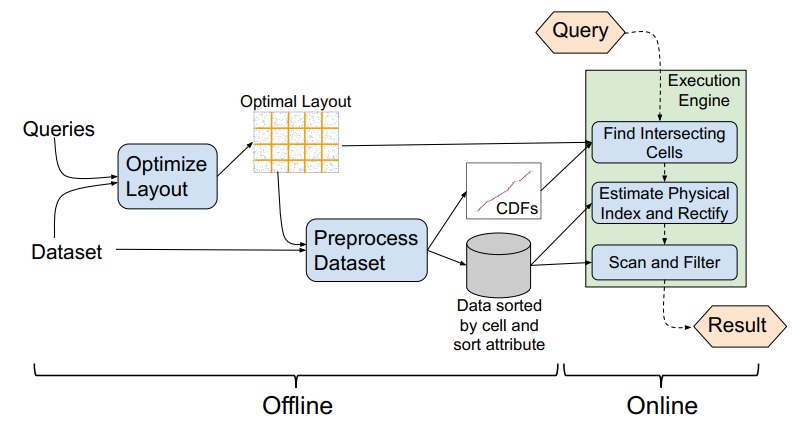
(1)离线预处理步骤,选择最佳布局,基于该布局创建索引;
(2)在线组件,负责在查询到达时执行查询。
Data Layout: Impose an ordering over the data
先对维度进行了排序,并使用前 $d-1$ 个维度创建一个 $d-1$ 维网格。每个维度的最小值($m_i$)和最大值($M_i$)之间被划分为 $c_i$ 个等间距的列,其中 $c_i$ 表示第 $i$ 个维度的列数。基于这个网格结构,每个数据点被映射到网格中的特定单元格,表示为一个由 $d-1$ 个属性组成的元组。
每个维度的范围计算方法为:
$$r_i = M_i - m_i + 1$$
每个数据点的位置计算公式为:
$$ cell(p) = (\lfloor {\frac{p_1-m_1}{r_1} \cdot c_1 } \rfloor,…, \lfloor {\frac{p_{d-1}-m_{d-1}}{r_{d-1}} \cdot c_{d-1} } \rfloor) $$
Basic Operation
Flood接收一个过滤器谓词作为输入,该谓词由一个或多个属性上的范围组成,并通过AND连接。这些范围的交集定义了一个超矩形,Flood可以准确地找到并处理这个超矩形中的点。
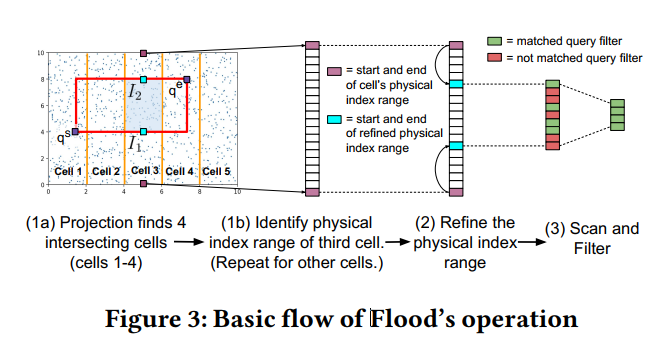
- Projection: 首先根据 $d-1$ 维的超矩形和网格求交集,得到相交的单元格
- Refinement: 再根据单元格表(记录每个单元格中第一个点的物理索引)将相交的每个单元格转换为一组组粗略的要扫描的物理索引范围,然后再依次将每个大范围缩到一个更细的范围
- Scan: 最后在小范围里进行逐个扫描。
Optimization of Layout Parameters
Cost Model
时间成本计算公式:
$$Time(D,q,L) = w_p N_c +w_r N_c + w_sN_s$$
- $N_c$ is the number of cells that fall within the query rectangle, and $w_p$ is the average time to perform projection on a single cell.
- $w_r$ is the average time to perform refinement on a cell.
- $N_s$ is the number of scanned points, and $w_s$ is the average time to perform each scan.
该公式估计了在给定布局L和查询q的情况下,在数据集D上执行查询所需的时间。根据这个公式,对于每个q的时间求平均,选择平均时间最小的那个布局L.

Flattening
Flattening(基于Recursive Model Index)将每个维度的数据值按照其cdf函数进行变换,使得每个单元格中包含的数据点数量大致相等,以避免某些单元格包含太多的数据点,从而提高查询性能。
Faster Refinement
用于加速查询的细化过程。通过对每个grid进行二分查找来实现的。为了避免二分查找成为瓶颈,Flood使用了一种称为“分段线性模型”的技术来加速细化过程:
- 将每个单元格的数据值按照一定的顺序进行排序,并将其分成若干个段。
- 对于每个段,使用一个线性模型来估计查询矩形在该段中的覆盖率。
在查询时先使用二分查找来确定查询矩形所在的段,然后使用线性模型来估计查询矩形在该段中的覆盖率。这样可以避免对每个单元格都进行二分查找,从而提高查询性能。
实验
Baselines
Clustered Single-Dimensional Index
- 主键索引叶子节点的值存储的就是MySQL的数据行(对应数据行的所有列的值,这意味着通过主键索引可以直接获取到完整的数据行,而无需进一步的查找或访问其他地方);普通索引(基于非主键列创建的索引)的叶子节点的值存储的是主键值和索引列的值,通过普通索引可以快速定位到符合索引条件的数据行的主键值,然后使用主键值再次查找对应的完整数据行。
- 找到了索引就找到了需要的数据,那么这个索引就是聚簇索引,所以主键就是聚簇索引,修改聚簇索引其实就是修改主键;索引的存储和数据的存储是分离的,也就是说找到了索引但没找到数据,需要根据索引上的值(主键)再次回表查询,非聚簇索引也叫做辅助索引
将数据行物理上按照索引的键值进行排序和存储,具有相邻键值的数据行在物理存储上也是相邻的,从而提高了数据的局部性和访问效率。
缺点是它们只能用于一个列,并且在某些情况下可能不适用。例如,如果查询需要同时使用多个列进行过滤或排序,聚簇单维索引可能无法提供最佳的性能。
Grid Files
Grid Files将数据点分配到网格单元格中,并不会优化针对特定查询工作负载。相邻的多个单元格中的数据点可能会存储在同一个存储桶中,并且数据点之间没有排序。作在高度倾斜的数据上,Grid Files算法的构建时间非常长。
Z-Order和UB-tree
UB树也使用Z值来索引点,但它不强加特定的点排序。相反,它根据点的Z值将其组织成树结构。
Z-Order索引找到查询矩形中包含的最小和最大Z值,并遍历在此范围内具有Z值的每个页面。这种方法需要扫描Z值范围内的所有页面,并检查落在查询矩形内的点。而UB树具有跳转至查询矩形中包含的下一个Z值的能力。这种优化使得UB树可以避免不必要的扫描,并可能减少查询过程中需要访问的页面数量。
k-d树
k-d树的主要优点是可以快速进行范围查询和最近邻搜索。在范围查询中,可以通过递归地在树中进行剪枝来快速确定落在给定范围内的数据点。在最近邻搜索中,可以使用树的结构和剪枝策略来减少搜索的空间,从而快速找到最接近给定查询点的数据点。
然而,k-d树的性能受到数据分布的影响。如果数据在某个维度上分布不均匀,可能会导致树的不平衡,影响查询性能。此外,k-d树对于高维数据可能会遇到维度诅咒问题,导致k-d树的性能下降。
当维度诅咒是指维度增加时,数据点在高维空间中的分布会呈现稀疏性,数据点之间的距离变得越来越大,导致在kd树中进行最近邻搜索时,需要遍历更多的节点才能找到最近邻点。这会导致kd树的搜索效率下降,因为大量的节点需要被访问,其中许多节点与查询点的距离可能并不接近。维度诅咒问题还会导致kd树的平衡性受到影响。在高维空间中,数据点分布的不均匀性增加,使得划分节点的选择变得困难,容易导致kd树的不平衡,进而影响查询性能。
数据集
作者提到他/她的目的是改善使用在多个属性列上谓词过滤的范围查询,所以在实验的过程中跳过了一些复杂如join、group by等操作
数据集包含了三个真实的工作负载和一合成的负载
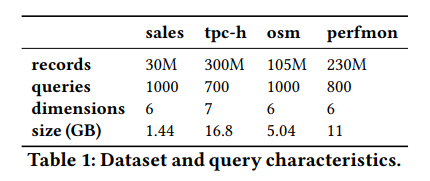
osm负载里涉及到了GPS坐标,查询使用1到3个维度,对时间戳、纬度和经度进行范围筛选,对记录类型和地标类别进行相等筛选。
perform数据集每个维度的数据都很不均匀,甚至可以说是高度偏斜。谓词的过滤包含了时间、计算机名称、CPU使用率、内存使用率、交换使用率和平均负载。
tpch的查询包括发货日期、收货日期、数量、折扣、订单密钥和供应商密钥的过滤器,并且执行SUM或COUNT聚合。
作者对每个数据集生成了同样数据分布的数据负载,包含训练、测试两种,并将训练集用作Flood的布局优化。
实验结果
实验围绕几个方面展开:
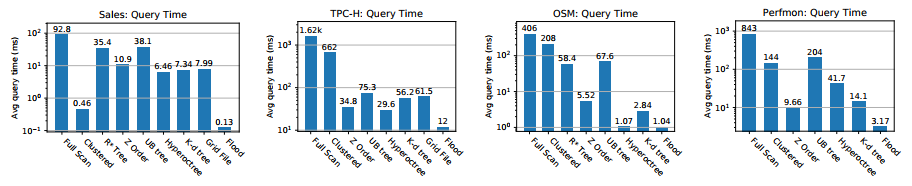
- 所有负载的执行时间,Query latency of Flood on all datasets. Flood’s index is trained automatically, while other indexes are manually tuned for optimal performance on each workload. We exclude the R∗-tree when it ran out of memory.
- 定制化负载(为了分析Flood所谓automatically的好处)。包含了纯OLTP、纯OLAP、HTAP、使用同纬度同选择度的单一类型查询负载、a workload with fewer dimensions (a strict subset) than indexed by the baseline indexes

- performance on dynamic query workload changes. 在每次负载变化的时候,Flood的性能都会下降,因为它没有针对新的工作负载进行训练;然而,一旦重新学习布局,它平均在5分钟内恢复,并在中值以5倍的优势击败次佳指数。
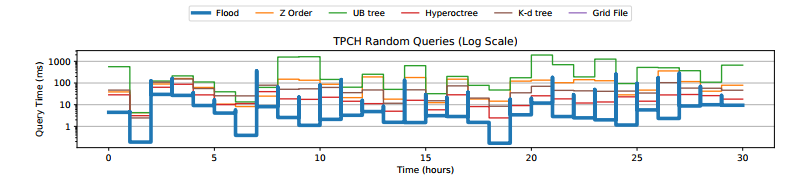
- 扫描开销:Flood的扫描开销比较小
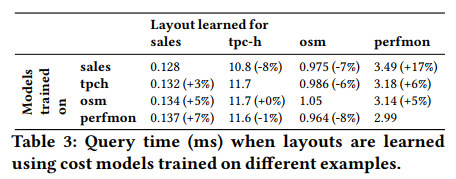
- robustness. 作者使用了生成的与数据集同数据分布的训练集生成了成本模型,并使用每个模型来学习所有四个数据集中的布局,然后在相应的查询工作负载上运行所有16个布局。结果表明无论使用哪个数据集来学习布局,生成的布局都具有相似的性能,它们之间的差异通常不到10%。
Scalability
这部分讨论了Flood如何随着数据集大小和查询选择性进行扩展。作者使用TPC-H数据集创建了较小的数据集,并测量了Flood在不同数据集大小和查询选择性下的平均查询时间。他们发现Flood的性能与数据集大小和查询选择性呈线性关系。此外,作者还展示了Flood的性能受其组件的影响,包括对最后一个索引维度进行排序、数据展平以及使用训练过程适应查询工作负载。