PAT甲级2016冬真题

算法哈希图论 Set AVL树

字数统计: 2k阅读时长: 11 min

 2023/08/29 

PAT考试真题解析

[1120] Friend Numbers (20)

set的应用

题目

Two integers are called “friend numbers” if they share the same sum of their digits, and the sum is their “friend ID”. For example, 123 and 51 are friend numbers since 1+2+3 = 5+1 = 6, and 6 is their friend ID. Given some numbers, you are supposed to count the number of different friend ID’s among them.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N. Then N positive integers are given in the next line, separated by spaces. All the numbers are less than $10^4$.

Output Specification:

For each case, print in the first line the number of different friend ID’s among the given integers. Then in the second line, output the friend ID’s in increasing order. The numbers must be separated by exactly one space and there must be no extra space at the end of the line.

注意点与解析

我的想法是用vis标记然后计数并排序，更好的方法是用set，把结果插⼊⼀个set集合中。因为set是有序的、不重复的，所以set的size值就是输出的个数， set中的每⼀个数字即所有答案的数字序列。

代码

vector<bool> vis(40, false);
vector<int> ans;

int calFriendId(int s) {
  int sum = 0;
  do {
    sum += s % 10;
    s /= 10;
  } while (s);
  return sum;
}

int main() {
  int n, cur;
  cin >> n;
  for (int i = 0; i < n; i++) {
    cin >> cur;
    int id = calFriendId(cur);
    vis[id] = true;
  }
  for (int i = 0; i < vis.size(); i++)
    if (vis[i])
      ans.push_back(i);
  cout << ans.size() << endl << ans[0];
  for (int i = 1; i < ans.size(); i++)
    cout << " " << ans[i];
  return 0;
}

[1121] Damn Single (25)

Map

题目

“Damn Single (单身狗)” is the Chinese nickname for someone who is being single. You are supposed to find those who are alone in a big party, so they can be taken care of.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer $N (≤ 50,000)$, the total number of couples. Then $N$ lines of the couples follow, each gives a couple of ID’s which are 5-digit numbers (i.e. from 00000 to 99999). After the list of couples, there is a positive integer $M (≤ 10,000)$ followed by M ID’s of the party guests. The numbers are separated by spaces. It is guaranteed that nobody is having bigamous marriage (重婚) or dangling with more than one companion.

Output Specification:

First print in a line the total number of lonely guests. Then in the next line, print their ID’s in increasing order. The numbers must be separated by exactly 1 space, and there must be no extra space at the end of the line.

注意点与解析

题目是不难，但是有几个注意点（卡了好一会）：
- 对于输出id这种事情，注意格式（比如要格式化输出五位），测试样例没有的话很容易忘记；
- 注意编号是从00000到99999，所以记录配偶的哈希数组不能初始化为0.不然会出错；
- 注意特判单身狗为0的情况。
注意来的客人分为有对象没来、有对象来了、没对象三种。
最后的ans数组也是可以改成set，省去排序。

代码

const int maxn = 1e6 + 10;
vector<int> companion(maxn, -1), ans, info;
vector<bool> guest(maxn, false);

int main() {
  int n, m, a, b;
  cin >> n;
  for (int i = 0; i < n; i++) {
    cin >> a >> b;
    companion[a] = b;
    companion[b] = a;
  }
  cin >> m;
  for (int i = 0; i < m; i++) {
    cin >> a;
    guest[a] = true;
    info.push_back(a);
  }
  for (auto p: info) {
    if (companion[p] == -1) {
      ans.push_back(p);
    } else {
      if (!guest[companion[p]])
        ans.push_back(p);
    }
  }
  sort(ans.begin(), ans.end());
  cout << ans.size();
  if (ans.size())  printf("\n%05d", ans[0]);
  for (int i = 1; i < ans.size(); i++)
    printf(" %05d", ans[i]);
  return 0;
}

[1122] Hamiltonian Cycle (25)

图论

题目

The “Hamilton cycle problem” is to find a simple cycle that contains every vertex in a graph. Such a cycle is called a “Hamiltonian cycle”.

In this problem, you are supposed to tell if a given cycle is a Hamiltonian cycle.

Input Specification:

Each input file contains one test case. For each case, the first line contains 2 positive integers $N (2<N≤200)$, the number of vertices, and $M$, the number of edges in an undirected graph. Then $M$ lines follow, each describes an edge in the format Vertex1 Vertex2, where the vertices are numbered from 1 to $N$. The next line gives a positive integer $K$ which is the number of queries, followed by $K$ lines of queries, each in the format:

$n$ $V_1$ $V_2$ $…$ $V_n$

where $n$ is the number of vertices in the list, and $V_i$’s are the vertices on a path.

Output Specification:

For each query, print in a line YES if the path does form a Hamiltonian cycle, or NO if not.

注意点与解析

给路径问这个路径是不是哈密尔顿回路，从图中的一个顶点出发，沿着边行走，经过图的每个顶点，且每个顶点仅访问一次，之后再回到起始点的一条路径，即需满足：
- 路径中顶点的个数需要是图顶点个数加上1（回到原点因此多一个），不能少走；
- 路径首尾需要是同一个顶点，回到原点；
- 需要经过每个顶点，不能重复走；
- 经过的路径存在。
因此在读入路径的每个顶点之后要判断总的个数是否满足要求，并判断最后一个是否等于第一个，但中间也许有重复的，因此可以将这些点插入set进行去重，之后判断set的大小是否刚好为图里顶点的个数即可。
这题如果对概念清楚的就不难。

代码

vector<vector<int>> G;

int main() {
  int n, m, v1, v2, k, cur, num;
  cin >> n >> m;
  G.resize(n + 1, vector<int>(n + 1, 0));
  for (int i = 0; i < m; i++) {
    cin >> v1 >> v2;
    G[v1][v2] = 1;
    G[v2][v1] = 1;
  }
  cin >> k;
  for (int i = 0; i < k; i++) {
    bool flag = true;
    cin >> num;
    vector<int> v(num);
    set<int> s;
    for (int j = 0; j < num; j++) {
      cin >> v[j];
      s.insert(v[j]);
    }
    if (s.size() != n || num != n + 1 || v[0] != v[num-1])  flag = false;
    for (int j = 0; j < num - 1; j++)
      if (!G[v[j]][v[j+1]]) flag = false;
    printf("%s\n", flag? "YES": "NO");
  }
  return 0;
}

[1122] Is It a Complete AVL Tree (30)

AVL树

题目

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

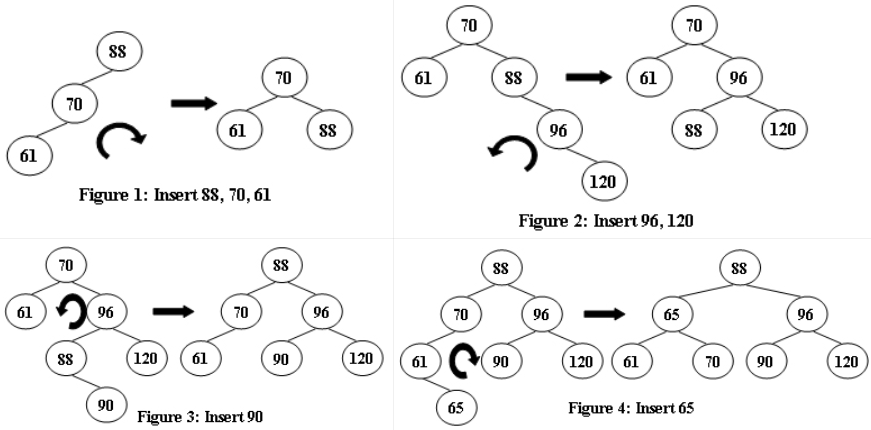
Now given a sequence of insertions, you are supposed to output the level-order traversal sequence of the resulting AVL tree, and to tell if it is a complete binary tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer $N (≤ 20)$. Then $N$ distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, insert the keys one by one into an initially empty AVL tree. Then first print in a line the level-order traversal sequence of the resulting AVL tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line. Then in the next line, print YES if the tree is complete, or NO if not.

代码

struct TreeNode {
  int val, height;
  TreeNode *left, *right;
} *root;
int n;

TreeNode* newNode(int x) {
  TreeNode *root = new TreeNode;
  root -> val = x;
  root -> height = 1;
  root -> left = root -> right = NULL;
  return root;
}

int getHeight(TreeNode *root) {
  if (!root)  return 0;
  else  return root -> height;
}

int getBalanceFactor(TreeNode *root) {
  return getHeight(root -> left) - getHeight(root -> right);
}

void updateHeight(TreeNode *root) {
  root -> height = max(getHeight(root -> left), getHeight(root -> right)) + 1;
}

void r_rotation(TreeNode* &root) {
  TreeNode* temp = root -> left;
  root -> left = temp -> right;
  temp -> right = root;
  updateHeight(root);
  updateHeight(temp);
  root = temp;
  return;
}

void l_rotation(TreeNode* &root) {
  TreeNode* temp = root -> right;
  root -> right = temp -> left;
  temp -> left = root;
  updateHeight(root);
  updateHeight(temp);
  root = temp;
  return;
}

void insert(TreeNode* &root, int k) {
  if (root == NULL) {
    root = newNode(k);
    return;
  }
  if (k < root -> val) {
    insert(root -> left, k);
    updateHeight(root);
    if (getBalanceFactor(root) == 2) {
      if (getBalanceFactor(root -> left) == 1)  // LL
        r_rotation(root);
      else if (getBalanceFactor(root -> left) == -1) {  // LR
        l_rotation(root -> left);
        r_rotation(root);
      }
    }
  } else {
    insert(root -> right, k);
    updateHeight(root);
    if (getBalanceFactor(root) == -2) {
      if (getBalanceFactor(root -> right) == -1)  // RR
        l_rotation(root);
      else if (getBalanceFactor(root -> right) == 1) {  // RL
        r_rotation(root -> right);
        l_rotation(root);
      }
    }
  }
  return;
}

bool flag = true;
void isCompleteTree(TreeNode *root, int x) {
  if (!root)  return;
  if (x > n)  flag = false;
  isCompleteTree(root -> left, 2 * x);
  isCompleteTree(root -> right, 2 * x + 1);
}

void levelTraversal(TreeNode* root) {
  if (!root)  return;
  queue<TreeNode*> q;
  q.push(root);
  int num = 0;
  while(!q.empty()) {
    TreeNode* cur = q.front();
    q.pop();
    cout << cur -> val;
    num++;
    if (num < n)  cout << " ";
    if (cur -> left)  q.push(cur -> left);
    if (cur -> right)  q.push(cur -> right);
  }
  return;
}

int main() {
  int cur;
  cin >> n;
  for (int i = 0; i < n; i++) {
    cin >> cur;
    insert(root, cur);
  }
  levelTraversal(root);
  isCompleteTree(root, 1);
  printf("\n%s", flag? "YES": "NO");
  return 0;
}

Next Post

Learning Multi-dimensional Indexes
Previous Post

PAT甲级2016秋真题