TUNIVERSE

PAT并查集笔记

算法 并查集
字数统计: 3.3k阅读时长: 15 min
2023/08/26

PAT考试并查集相关笔记

前置知识

并查集是一种维护集合的数据结构，支持两种操作：① 合并两个集合（合并）；② 判断某两个元素是否在一个集合（查找）。

使用 father[i] 数组来表示当前元素的父亲，如果 father[i] == i 则说明元素i是该集合的根结点。对于同一个集合来说只存在一个根结点，且将其作为所属集合的标识。

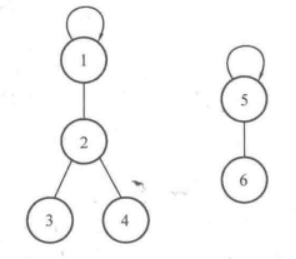
example

基本操作

先初始化father根结点数组，然后再根据需要进行查找和合并操作

初始化

一开始每个元素都是独立的集合，因此需要令所有 father[i] = i；

1
2
for (int i = 1; i <= n; i++)
  father[i] = i;

查找

由于规定同一个集合只存在一个根结点，因此查找操作就是对给定的结点寻找其根结点的过程。实现的方式可以是递归或者递推，反复寻找父亲结点，直到找到根结点。

1
2
3
4
5
6
7
8
9
10
11
12
// 递推
int findFather(int x) {
  while (x != father[x])
    x = father[x];
  return x;
}

// 递归
int findFather(int x) {
  if (x == father[x]) return x;
  else  return findFather(father[x]);
}

合并

合并是指把两个集合合并成一个，一般给出两个元素，要求把这两个元素所在的集合合并。

一般是先判断两个元素是否属于同一个集合，只有当两个元素属于不同集合时才合并，而合并的过程一般是把其中一个集合的根结点的父亲指向另一个集合的根结点，即对于这两个元素集合的根结点 faA 和 faB，令 father[faA] = faB 或者 father[faB] = faA。

要进行判断是否属于同一个集合的原因是因为，只对两个不同的集合进行合并可以保证同一个集合中一定不会产生环，即并查集产生的每一个集合都是一棵树。

1
2
3
4
5
6
7
void Union(int a, int b) {
  int faA = findFather(a);
  int faB = findFather(b);
  if (faA != faB)
    father[faA] = faB;
  return;
}

路径压缩

将查询结点路径上的所有结点的父亲都指向根结点，查找的时候就不需要一直回溯找父亲，查询的复杂度降为 $O(1)$

转换的过程可以概括为两个步骤：

  • 按原先的写法获得x的根结点r；
  • 重新从x开始走一遍寻找根结点的过程，把路径上经过的所有的结点的父亲全部改为根结点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 递推
int findFather(int x) {
  int a = x;  // 保存起点值
  while (x != father[x]) {  // 寻找根结点
    x = father[x];
  }
  while (a != father[a]) {
    int z = a;
    a = father[a];  // 回溯父结点
    father[z] = x;  // 将原先的结点a的父亲改为根结点x
  }
  return x;
}

// 递归
int findFather(int x) {
  if (x == father[x]) return x;
  else {
    int F = findFather(father[x]);
    father[x] = F;
    return F;
  }
}

[例题] 好朋友

题目

有一个叫作“数码世界”的奇异空间，在数码世界里生活着许许多多的数码宝贝，其中有些数码宝贝之间可能是好朋友。并且数码世界有两条不成文的规定:

第一，数码宝贝A和数码宝贝B是好朋友等价于数码宝贝B和数码宝贝A是好朋友。
第二，如果数码宝贝A和数码宝贝C是好朋友，而数码宝贝B和数码宝贝C也是好朋友，那么A和B也是好朋友。

现在给出这些数码宝贝中所有好朋友的信息，问:可以把这些数码宝贝分成多少组，满足每组中的任意两只数码宝贝都是好朋友，且任意两组之间的数码宝贝都不是好朋友。

注意点与解析

  • 多少个连通图、森林个数（每个集合都是一棵树）
  • 可以把题目中的“组”视为集合，而题目中给出的好朋友关系视为两个结点之间的边，那么在输入这些好朋友关系时就可以同时对它们进行开查集的合并操作，这样在处理完毕后就能得到一些集合，而集合的个数就是要求的组数。
  • 至于集合个数的求解，需要用到本节最开始时讲解过的知识:“对同一个集合来说只存在一个根结点，且将其作为所属集合的标识”。因此可以开一个bool型数组 fag[N] 来记录每个结点是否作为某个集合的根结点，这样当处理完输入数据之后就可以遍历所有元素，令它所在集合的根结点的 flag 值设为 true。最后累加 flag 数组中的元素即可得到集合数目。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
vector<int> father;
vector<bool> isRoot;

void init(int n) {
  for (int i = 1; i <= n; i++)
    father[i] = i;
  return;
}

void Union(int a, int b) {
  int faA = findFather(a);
  int faB = findFather(b);
  if (faA != faB)
    father[faA] = father[faB];
  return;
}

int findFather(int x) {
  int a = x;
  while (x != father[x])
    x = father[x];
  while (a != father[a]) {
    int z = a;
    a = father[a];
    father[z] = x;
  }
  return x;
}

int main() {
  int n, m, a, b;
  cin >> n >> m;
  father.resize(n + 1);
  isRoot.resize(n + 1, false);
  init(n);
  for (int i = 0; i < m; i++) {
    cin >> a >> b;
    Union(a, b);
  }
  for (int i = 1; i <= n; i++)
    isRoot[findFather(i)] = true; // 注意是findFather(i)
  int ans = 0;
  for (int i = 1; i <= n; i++)
    ans += isRoot[i];
  cout << ans;
  return 0;
}

[1107] Social Clusters

题目

When register on a social network, you are always asked to specify your hobbies in order to find some potential friends with the same hobbies. A social cluster is a set of people who have some of their hobbies in common. You are supposed to find all the clusters.

Input Specification:

Each input file contains one test case. For each test case, the first line contains a positive integer $N (≤1000)$, the total number of people in a social network. Hence the people are numbered from 1 to $N$. Then $N$ lines follow, each gives the hobby list of a person in the format:

$K_i$ : $h_i[1]$ $h_i[2]$ $…$ $h_i[K_i]$

where $K_i(>0)$ is the number of hobbies, and $h_i[j]$ is the index of the $j$-th hobby, which is an integer in [1, 1000].

Output Specification:

For each case, print in one line the total number of clusters in the network. Then in the second line, print the numbers of people in the clusters in non-increasing order. The numbers must be separated by exactly one space, and there must be no extra space at the end of the line.

注意点与解析

  • 判断两个人是好朋友的条件为他们有公共喜欢的活动，因此不妨开一个数组 course，其中 course[h] 用以记录任意一个喜欢活动 h 的人的编号，这样的话findFather(course[h]) 就是这个人所在的社交网络的根结点。于是，对当前读入的人的编号 i 和他喜欢的每一个活动 h，只需要合并 i 与 findFather(course[h]) 即可。
  • cin 用多了别忘了 scanf()，可以按格式输入。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
vector<int> father, isRoot;

int findFather(int x) {
  int a = x;
  while(x != father[x])
    x = father[x];
  while(a != father[a]) {
    int z = a;
    a = father[a];
    father[z] = x;
  }
  return x;
}

void union2(int a, int b) {
  int fa = findFather(a);
  int fb = findFather(b);
  if (fa != fb) father[fa] = fb;  // a -> b
  return;
}

int main() {
  int n, k, ans = 0;
  cin >> n;
  father.resize(n + 1);
  isRoot.resize(n + 1, false);
  vector<int> course(1001, 0);

  for (int i = 1; i <= n; i++)  father[i] = i;
  for (int i = 1; i <= n; i++) {
    scanf("%d:", &k);
    int a;
    for (int j = 0; j < k; j++) {
      cin >> a;
      if (course[a] == 0) course[a] = i;
      union2(i, findFather(course[a]));
    }
  }
  for (int i = 1; i <= n; i++)  isRoot[findFather(i)]++;
  for (int i = 1; i <= n; i++)
    if (isRoot[i] != 0) ans++;

  sort(isRoot.begin(), isRoot.end(), [&](int a, int b) {
    return a > b;
  });
  cout << ans << endl;
  for (int i = 0; i < ans; i++) {
    cout << isRoot[i];
    if (i != ans - 1)  cout << " ";
  }
  return 0;
}

[1013] Battle Over Cities

题目

It is vitally important to have all the cities connected by highways in a war. If a city is occupied by the enemy, all the highways from/toward that city are closed. We must know immediately if we need to repair any other highways to keep the rest of the cities connected. Given the map of cities which have all the remaining highways marked, you are supposed to tell the number of highways need to be repaired, quickly.

For example, if we have 3 cities and 2 highways connecting $city_1$-$city_2$ and $city_1$-$city_3$. Then if $city_1$ is occupied by the enemy, we must have 1 highway repaired, that is the highway $city_2$-$city_3$.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 3 numbers $N (<1000)$, $M$ and $K$, which are the total number of cities, the number of remaining highways, and the number of cities to be checked, respectively. Then $M$ lines follow, each describes a highway by 2 integers, which are the numbers of the cities the highway connects. The cities are numbered from 1 to $N$. Finally there is a line containing $K$ numbers, which represent the cities we concern.

Output Specification:

For each of the K cities, output in a line the number of highways need to be repaired if that city is lost.

注意点与解析

  • 判断无向图每条边的两个顶点是否在同一个集合内，如果在同一个集合内，则不做处理;否则，将这两个顶点加入同一个集合。最后统计有集合的个数即可。
  • 这题必须得做路径压缩，否则最后一个测试点会超时，建议以后没有特殊情况都把路径压缩给写上。

代码

这题还有个DFS解法，在图一文的笔记里有提及，可以直观对比一下执行时间：

这是DFS

time1

这是并查集

time2

以下是并查集代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
int n, m, k;
vector<vector<int>> G;
vector<bool> vis;
vector<int> father;

int findFather(int x) {
  int a = x;
  while (x != father[x])
    x = father[x];
  while (a != father[a]) {
    int z = a;
    a = father[a];
    father[z] = x;
  }
  return x;
}

void Union(int a, int b) {
  int faA = findFather(a);
  int faB = findFather(b);
  if (faA != faB)
    father[faA] = father[faB];
  return;
}

void init() {
  for (int i = 1; i <= n; i++) {
    father[i] = i;
    vis[i] = false;
  }
  return;
}

int main(){
  cin >> n >> m >> k;
  vis.resize(n + 1);
  father.resize(n + 1);
  G.resize(n + 1);

  int a, b, cur;
  for (int i = 0; i < m; i++) {
    cin >> a >> b;
    G[a].push_back(b);
    G[b].push_back(a);
  }
  for (int i = 0; i < k; i++) {
    cin >> cur;
    init();
    for (int v = 1; v <= n; v++) {
      for (auto u: G[v]) {
        if (v == cur || u == cur) continue;
        Union(v, u);
      }
    }
    int ans = 0;
    for (int j = 1; j <= n; j++) {
      if (j == cur) continue;
      int fa_j = findFather(j);
      if (vis[fa_j] == false) {
        ans++;
        vis[fa_j] = true;
      }
    }
    cout << ans - 1 << endl;
  }
  return 0;
}

[1021] Deepest Root

题目

A graph which is connected and acyclic can be considered a tree. The height of the tree depends on the selected root. Now you are supposed to find the root that results in a highest tree. Such a root is called the deepest root.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer $N (≤10^4)$ which is the number of nodes, and hence the nodes are numbered from 1 to $N$. Then $N−1$ lines follow, each describes an edge by given the two adjacent nodes’ numbers.

Output Specification:

For each test case, print each of the deepest roots in a line. If such a root is not unique, print them in increasing order of their numbers. In case that the given graph is not a tree, print Error: K components where K is the number of connected components in the graph.

注意点与解析

  • ⾸先深度优先搜索判断它有⼏个连通分量。如果有多个，那就输出 Error: x components，如果只有⼀个，就两次深度优先搜索，先从⼀个结点dfs后保留最⾼⾼度拥有的结点们，然后从这些结点中的其中任意⼀个开始dfs得到最⾼⾼度的结点们，这两个结点集合的并集就是所求；
  • 注意第二次dfs之前要保存第一次dfs得到的结果，因为第二次dfs时height可能会超过第一次，temp数组会被清空一次；
  • 这题还有个很重要的点是题目保证了只有N-1条边，因此绝对是一棵树；
  • 使用 set 的话最后可以不进行去重和排序，用邻接矩阵会超内存所以这题只能用邻接表存储；
  • 算法笔记配套习题上的dfs里面写了一个所谓的前一个结点参数，和用vis数组标记的效果是一样的，都是为了防止无向图里走回头路。

代码

用纯DFS也能做，在图相关的笔记里写了解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
int n, maxh = 0;
set<int> s;
vector<bool> isRoot, vis;
vector<int> father, temp;
vector<vector<int>> G;

void dfs(int node, int height) {
  if (height > maxh) {
    temp.clear();
    temp.push_back(node);
    maxh = height;
  } else if (height == maxh) {
    temp.push_back(node);
  }
  vis[node] = true;
  for (auto v: G[node])
    if (vis[v] == false)
      dfs(v, height + 1);
  return;
}

int findFather(int x) {
  int a = x;
  while (x != father[x])
    x = father[x];
  while (a != father[a]) {
    int z = a;
    a = father[a];
    father[z] = x;
  }
  return x;
}

void Union(int a, int b) {
  int fa_a = findFather(a);
  int fa_b = findFather(b);
  if (fa_a != fa_b)
    father[fa_a] = father[fa_b];
  return;
}

void init() {
  for (int i = 1; i <= n; i++)
    father[i] = i;
  return;
}

int main() {
  cin >> n;
  vis.resize(n + 1, false);
  isRoot.resize(n + 1, false);
  father.resize(n + 1);
  G.resize(n + 1);
  init();

  int a, b;
  for (int i = 0; i < n - 1; i++) {
    cin >> a >> b;
    G[a].push_back(b);
    G[b].push_back(a);
    Union(a, b);
  }

  // calculate blocks
  int ans = 0;
  for (int i = 1; i <= n; i++)
    isRoot[findFather(i)] = true;
  for (int i = 1; i <= n; i++)
    ans += isRoot[i];

  if (ans > 1) {
    printf("Error: %d components", ans);
  } else {
    dfs(1, 1);
    for (auto p: temp)  s.insert(p);
    fill(vis.begin(), vis.end(), false);
    dfs(temp[0], 1);
    for (auto p: temp)  s.insert(p);
    for (auto p: s) cout << p << endl;
  }
  return 0;
}
CATALOG
  1. 1. 前置知识
    1. 1.1. 基本操作
      1. 1.1.1. 初始化
      2. 1.1.2. 查找
      3. 1.1.3. 合并
      4. 1.1.4. 路径压缩
  2. 2. [例题] 好朋友
    1. 2.1. 题目
    2. 2.2. 注意点与解析
    3. 2.3. 代码
  3. 3. [1107] Social Clusters
    1. 3.1. 题目
      1. 3.1.1. Input Specification:
      2. 3.1.2. Output Specification:
    2. 3.2. 注意点与解析
    3. 3.3. 代码
  4. 4. [1013] Battle Over Cities
    1. 4.1. 题目
      1. 4.1.1. Input Specification:
      2. 4.1.2. Output Specification:
    2. 4.2. 注意点与解析
    3. 4.3. 代码
  5. 5. [1021] Deepest Root
    1. 5.1. 题目
      1. 5.1.1. Input Specification:
      2. 5.1.2. Output Specification:
    2. 5.2. 注意点与解析
    3. 5.3. 代码
Total : 65
2024
2023
2022
2021
2020
动态规划 计算机视觉 三维重建 深度学习 查找 教程 MongoDB 数据库 Neo4j MySQL 机器学习 GNN 随笔 托福 故障诊断 Greenplum操作 Linux磁盘扩容 debug记录 环境问题 多维索引 磁盘故障 迁移学习 列存分区 链表 LeetCode 双指针 剪枝 素数 逻辑题 并查集 树的遍历 哈希 字符串 排序 二叉搜索树 数学模拟 图论 完全二叉树 最短路径 贪心 Set AVL树 图模拟 DFS 快乐模拟 拓扑排序 栈 图的遍历 递推 前端 React Webpack Eslint top
算法 华科课程 学习笔记 英语 年末总结 腾讯AI训练营