2023春计算机视觉结课作业,文献综述
$\mathcal{1} \space 介绍$
三维重建是一种计算机视觉技术,旨在从二维图像或视频中推导出三维场景或物体的形状和结构。
2014年以前的传统方法的技术侧重点往往在于数学的立体几何,通常需要大量手动操作和专业知识,并且由于需要使用多个传感器来获取数据,这些方法往往会受到各种因素的干扰和限制,难以处理复杂场景。如$Laurentini$$[1]$提出的基于轮廓的视觉壳体方法,对于透明物体其重建效果会比较差;此外,该方法也需要准确的轮廓提取,对于物体表面存在遮挡、纹理不清晰等情况时,其重建效果也会受到影响。$Hartley$和 $Zisserman$$[2]$提出的传统多视图几何方法只能使用几何信息进行重建,除了对噪声、缺失数据和误匹配等问题比较敏感外,对于非刚性或非刚性变形的物体,其重建效果会受到很大的限制。
而自2014年,$David$$[7]$等人基于体素的形式,将单张RGB图像作为输入,直接使用神经网络进行深度图恢复,开启了将深度学习方法应用于三维重建领域的大门。此后,深度学习开始被广泛运用在三维重建问题上且在之后的数年里被广泛证实十分有效。目前深度学习技术在三维重建领域的应用已经取得了很大的进展,并且在许多应用领域中都有着广泛的应用前景,例如机器人、自主导航、图形和娱乐等方面。本文选取了几种应用于三维重建的深度学习方法,对每种方法的相关技术进行分类(章节$2.2$)介绍、梳理与回顾(章节$3$),将各个方法进行比较并给出各个方法的优缺点(章节$4$)。
$\mathcal{2} \space 问题描述和分类$
$\mathcal{2.1} \space 问题描述$
三维重建的问题可以描述为如下数学公式
$$Input: I = { I_{k}, k = 1, …, n } ;$$
$$Loss \space function: \mathcal{L}(I) = d(f_{\theta}(I), X)$$
其中,
- $I$ 代表一个或多个物体 $X$ 的一组数目 $n \geq 1$ 的RGB图像;
- $f_{\theta}$ 代表预测器,其中 $\theta$ 是 $f$ 的参数集合,$d(.\space,\space.)$ 是目标输出 $X$ 和重建输出 $\hat{X}$ 之间距离的度量方式;
- $f_{\theta}$ 的目标是通过输入 $I$ 构建出最接近目标 $X$ 的 $\hat{X}$,即我们训练的目的是使得 $d(f_{\theta}(I), X)$ 的值达到最小。
$\mathcal{2.2} \space 分类$
在$Han$$[3]$等人的文章中提到了一种基于深度学习的三维重建的分类方法。该方法根据输入、输出表示、深度神经网络架构、训练过程和监督程度等方面进行分类。具体来说,输入可以是单个图像、多个图像或视频流;输出表示可以是点云、体素或网格;深度神经网络架构可以是卷积神经网络(CNN)、生成对抗网络(GAN)等;训练过程可以是有监督的、无监督的或半监督的;监督程度可以是单一物体或多个物体,以及统一背景或杂乱背景。
本文所选取的各种方法将按照其解码器输出数据格式进行分类,具体即体素、点云和网格
- 体素,可以看作是一个立方体元素。通过将三维空间划分为许多小的立方体单元,可以将物体的几何形状表示为一个三维模型。
- 点云,由一组三维坐标点构成的集合,每个点代表物体表面上的一个采样点。通过将物体表面上的所有采样点表示为一个点云,可以将物体的几何形状表示为一个无序的三维坐标集合。
- 网格,由一组三角形或四边形面片构成的集合,每个面片代表物体表面上的一个小区域。通过将物体表面上的所有小区域表示为一个网格,可以将物体的几何形状表示为一个有序的三角形或四边形面片集合。
$\mathcal{3} \space 方法梳理$
本章节选取了一些基于深度学习的三维重建方法,按照章节$2.2$提到的输出数据格式进来分类介绍和详细分析。
$\mathcal{3.1} \space 体素$
本部分选取了$Choy$$[4]$提出的3D-R2N2网络架构、$Park$$[5]$提出的DeepSDF技术以及$Varol$$[6]$提出的一种叫做BodyNet的神经网络结构进行介绍。
$\mathcal{3.1.1} \space 3D-R2N2$
本篇文章提出了一种基于LSTM和GRU网络的循环神经网络的新型架构,称为3D Recurrent Reconstruction Neural Network(3D-R2N2),网络的目标是实现单视角和多视角的三维重建。该网络由三个部分组成:一个由二维卷积神经网络构成的编码器、一种名为三维卷积LSTM的新型架构和一个由三维反卷积神经网络构成的解码器。给定来自任意视角的一个或多个物体的图像,编码器将每个输入图像 $x$ 编码为低维特征 $T(x)$;然后,3D卷积LSTM单元通过选择性地更新它们的细胞状态或通过关闭输入门来保留状态;最后,解码器解码LSTM单元的隐藏状态并生成三维概率体素重建结果。总体结构如图1所示。
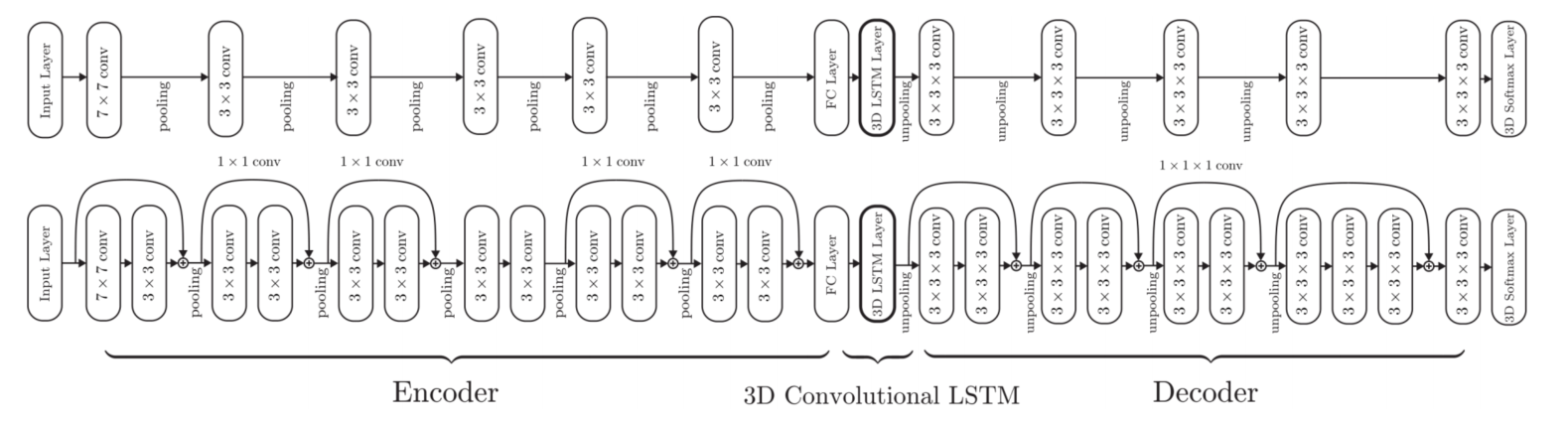
编码器有标准前馈CNN网络和深度残差变体两种:
- 标准前馈CNN由标准卷积层、池化层和Leaky ReLU激活函数组成,最后接一个全连接层,可以将输入图像转换为高维特征向量;
- 深度残差变体是在标准前馈CNN的基础上进行改进的。它添加了残差连接来解决深度神经网络中梯度消失和梯度爆炸等问题。具体来说,每个残差块包含两个卷积层和一个跳跃连接,可以将输入直接传递到输出中。
3D-Convolutional-LSTM根据有无输出门有以下两种。在每个时间步骤中,每个LSTM单元接收来自编码器的相同特征向量以及其邻居的隐藏状态作为输入。这些输入通过一个3×3×3卷积核进行卷积操作,并传递给LSTM单元进行处理。然后,LSTM单元将其输出传递给下一个时间步骤,并将其隐藏状态传递给其邻居。在没有输出门的版本中,LSTM单元直接将其隐藏状态作为输出。而在带有输出门的GRU版本中,LSTM单元还会根据当前输入和先前隐藏状态计算一个输出门,并使用该门来控制其输出。
解码器使用一个全连接层将中间表示转换为一个低分辨率3D体素模型;然后使用多个反卷积层来逐步增加输出分辨率,并生成更高分辨率的3D体素模型;最后,使用一个Sigmoid激活函数将输出限制在0到1之间。同时在训练过程中,为了提高网络性能并减少过拟合现象,模型使用了Progressive Growing的技术来逐步增加输入图像分辨率和输出网格分辨率。
$\mathcal{3.1.2} \space DeepSDF$
与上一种方法的输入为2D图像不同的是,DeepSDF的输入也是三维的,因为它是一种用于处理三维几何图形的方法。本篇文章中定义了一种叫做有符号距离函数(Signed Distance Functions,后简称SDF)的连续函数,对于给定的空间点,输出该点到最近表面的距离,并用符号表示该点在表面内部或外部。基于此,将问题转换为使用深度神经网络直接回归点样本的连续SDF,形成一个决策边界作为三维几何图形的表面,对点做在表面外或内的二元分类,从而生成新的几何模型。如图2所示。
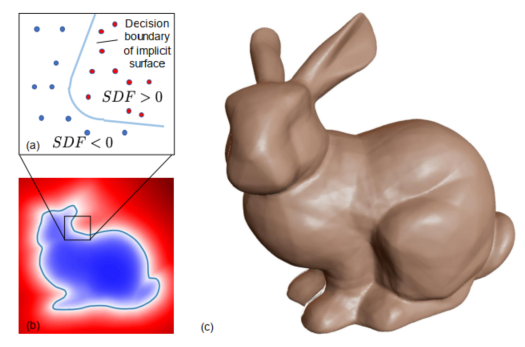
SDF定义公式如下:
$$SDF(\mathbf{x}) = s : \mathbf{x} \in \mathbb{R}^3 , \space s \in \mathbb{R}. $$
对于给定的三维空间点 $x$,$SDF(x)$ 表示该点到最近表面的距离,并且根据该点在表面内部或外部的位置标定正负号。其中,$s$ 表示 $x$ 到最近表面的距离,如果 $x$ 在表面内部,则 $s$ 为负数;如果 $x$ 在表面外部,则 $s$ 为正数。
用来生成连续SDF所使用的模型,其结构是一种前馈神经网络。训练该网络的目标是,对于给定的空间坐标和其SDF值:
$$ X := {(\mathbf{x}, s) : SDF(\mathbf{x}) = s }.$$
可以训练出一个神经网络模型 $f_{\theta}$,使得在任意一个目标域中:
$$ f_{\theta}(\mathbf{x}) \approx SDF(\mathbf{x}), \space \forall \mathbf{x} \in \Omega. $$
而按照功能分,模型则可以分为编码器和解码器两部分,都是由多个卷积层和池化层交替堆叠,再加上全连接层构成。
为了适应不同的应用场景,文章中提出了两种形状表示方式 1)单形状DeepSDF 2)编码形状DeepSDF。
- 单形状DeepSDF适用于对单个形状进行建模和重建的场景。在这种情况下,只需要训练一个神经网络来表示该形状的连续有符号距离函数,并使用该网络来生成新的几何形状。
- 编码形状DeepSDF适用于对多个相关形状进行建模和重建的场景。在这种情况下,就需要找到一些共同属性,并将它们嵌入到低维潜在空间中。通过学习潜在空间和对应的连续有符号距离函数,以生成新的几何形状,并且可以通过修改代码向量来控制生成的几何形状。
因此,在单形状DeepSDF中,编码器的输入是一个三维点坐标 $(x,y,z)$,其输出潜在向量 $z$ 作为解码器的输入,最终输出SDF;在编码形状DeepSDF中,编码器的输入是一个三维点坐标 $(x,y,z)$ 和一个控制生成几何形状的代码向量 $c$ 的拼接,其输出潜在向量 $z$ 和前面提到的三维点坐标一起作为解码器的输入,最终输出SDF。
$\mathcal{3.1.3} \space BodyNet$
本文介绍了一种名为BodyNet的神经网络,它可以从单个图像中直接推断出三维人体形状。与上面两种方法不同的是,该网络的设计旨在解决视频编辑、动画和时尚等领域中的人体模型估计问题。BodyNet包括四个自网络,分别是二维姿态估计子网络、二维深体部位分割子网络、三维姿态估计子网络以及三维形状估计子网络。每个子网络都是由一个沙漏结构构成,其是一种常用的卷积神经网络结构,由编码器和解码器组成,可以有效地提取特征并保留空间信息。其中编码器将输入图像转换为特征向量,解码器将特征向量转换回三维体积表示。
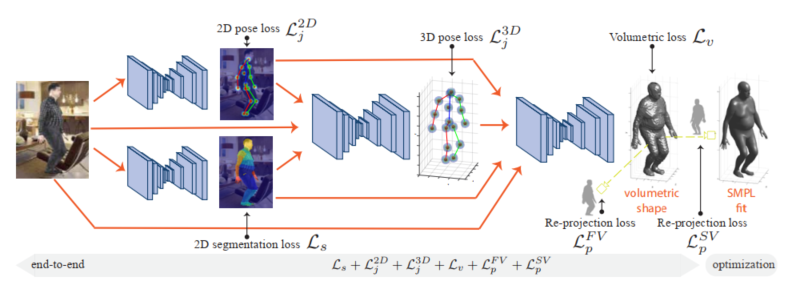
BodyNet中通过四个子网结构来处理不同任务,并共享特征以提高整个系统的性能,各个子网络之间通过特征融合和级联的方式进行联合。输入RGB图像后,首先经过二维姿态估计子网络和二维身体部位分割子网络,得到对应的二维姿态估计结果和身体部位分割掩模。然后将这些结果与RGB图像特征一起输入到三维姿态估计子网络中,得到对应的三维姿态估计结果。最后,将三维姿态估计结果与身体部位分割掩模一起输入到体积重建子网络中,得到对应的三维人体形状。在这个过程中,每个子网络都有自己的损失函数,并且各自通过反向传播算法来更新自己的权重和共享层的权重,最后各个损失函数通过加权平均的方式进行特征融合和级联。
$\mathcal{3.2} \space 点云$
本部分选取了$Li$$[8]$所使用的变形向量场方法、$Insafutdinov$$[9]$使用的一种基于无监督学习的方法和 $Li$$[10]$基于基于深度形状先验和轮廓的方法进行介绍。
$\mathcal{3.2.1} \space Using \space Deformation \space Vector \space Fields$
这篇文章提出了一种新型的单视角3D物体重建方法,主要分为深度图预测和点云重建两个步骤。
深度图预测阶段,使用了U-Net作为编码器-解码器的结构基础。模型输入一张RGB图像在U-Net中进行特征提取和编码,然后再解码器部分使用反卷积层和上采样层将特征图还原为深度图。同时,还在解码器中引入了残差块的使用,以保留更多的细节,最后输出物体的深度图(一种灰度图,其中每个像素表示该点到相机的距离)。
点云重建阶段,作者定义了一个规则的二维网络,并将深度图上的每个像素点映射到该网格上;然后,使用变形向量场对该网格进行变形,并将变形后的网格中的每个像素点映射回深度图上;最后,通过将深度图上的像素点和它们在变形后的网格中对应的位置一一配对,得到一个点云表示。在这个过程中,变形向量场起到了关键作用。变形向量场是一种二维向量场,它描述了物体表面上每个像素点的变形情况。在本文中,对于每个像素点都计算出一个变形向量,该向量表示从深度图中的一个像素点到点云中对应点的偏移量。
在训练阶段,作者使用了一种组合的损失函数,它包括了单视角损失和多视角一致性损失,公式如下。其中,$L_{single}$表示单视角损失,$L_{multi}$表示多视角一致性损失,$λ1$和$λ2$是两个超参数,用于控制两个损失函数的权重。
$$L = λ1 * L_{single} + λ2 * L_{multi}$$
具体如下:
- 单视角损失:先将真实点云投影到深度图上,并计算每个像素点到最近点的距离。然后,将预测点云投影到同样的深度图上,并计算每个像素点到最近点的距离。最后,我们可以通过计算这些距离之间的平均值来得到单视角损失。
- 多视角一致性损失:先将预测点云投影到多个视角上,并计算每个视角下的距离场。然后,对于每个像素点,在所有视角下计算其距离场的平均值。最后,通过计算预测点云和真实点云之间的距离误差,并将其乘以距离场的平均值来得到多视角一致性损失。
$\mathcal{3.2.2} \space Based \space on \space Unsupervised \space Learning$
本文提出了一种使用可微分点云的无监督学习方法,用于从未标记类别的特定图像集合中学习准确的3D形状以及相机的位置和方法(原文中叫做camera pose,后翻译为相机姿态)。模型由三个部分组成:一个用于预测物体的3D形状,一个用于预测相机姿态,和一个将点云渲染为图像的点云渲染器。模型总体框架如下图中的(b)所示;图(a)则展示了物体从不同的角度观察时,投影非常相似而导致相机的位置和方向存在多种可能性的问题。
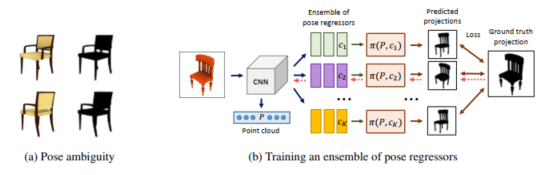
物体3D形状预测部分,模型包括一个卷积神经网络和一个多层感知器。模型接收两张相同物体的RGB图像作为输入,在CNN中使用具有不同步长的卷积核进行特征提取,提取后的特征被送入MLP进行进一步处理和预测。最终,该模型输出一个点云表示物体3D形状。
相机姿态预测部分,模型也是由一个卷积神经网络和一个多层感知器组成,该模型接收两张RGB图像作为输入,并输出一个四元数表示相机在该图像中的姿态,这个四元数可以用来计算相机在三维空间中的位置和方向。这个模型和上面做物体形状预测的模型共享大部分CNN的参数,这使得模型可以同时预测物体的3D形状和相机姿态,并且可以更好地利用训练数据进行训练。
此外,本模型还使用了一个可微分的点云渲染器来将预测的3D形状和相机姿态转换为图像,渲染器简称为$π$。$π$使用了一种称为“投影”的技术来将点云转换为图像,它将每个点在三维空间中投影到二维平面上,并根据其距离和颜色值在该平面上生成一个像素。这其中使用了前面模型的点云图和生成的相机姿态矩阵,投影转换的过程中涉及到了相机的焦距、主点和像素大小等信息,并使用双线性插值来计算每个像素的颜色值。
最终生成的这个图像可以与真实图像进行比较,以计算模型预测的准确性。由于$π$是可微分的,因此它可以与CNN一起训练,用MSE计算损失并且可以通过反向传播算法来计算梯度,这使得模型可以同时学习如何预测物体3D形状、相机姿态和如何将它们转换为图像。也正是其可以将点云最终转换为图像,才实现了仅通过最小化预测图像与真实图像之间的差异来训练模型的无监督学习。
$\mathcal{3.2.3} \space Using \space Deep \space Shape \space Prior \space and \space Silhouette$
本文提出了一种基于深度学习的单张图像3D物体重建方法,并引入了形状先验和姿态参数等技术细节来提高重建结果的准确性和稳定性。
深度自编码器使用卷积神经网络来学习3D物体形状的潜在编码。该自编码器由一个编码器和一个解码器组成,其中编码器由多个卷积层和全连接层组成,将输入图像映射到潜在空间中的低维表示。解码器则由多个反卷积层和全连接层组成,将这些表示映射回3D物体形状。
$$z = f_{\theta_e}(x)$$
$$\hat{x} = f_{\theta_d}(z)$$
其中,$x$为输入图像,$z$为潜在空间中的低维表示,$\hat{x}$为重建后的图像,$f_{\theta_e}$和$f_{\theta_d}$分别为编码器和解码器。
概率形状先验,为了更好地约束三维重建过程以提高重建质量,模型引入了一种叫概率形状先验的概率分布。该概率分布是一个高斯分布,均值为0向量,协方差矩阵为对角线矩阵,公式如下。通过将这个概率分布与深度自编码器输出的潜在编码相结合,并加上一定的权重系数来控制其影响力大小。
$$p(z) = \mathcal{N}(z|0,\Sigma)$$
在模型训练和优化的过程中作者也考虑到了使用概率分布,将重建误差和前面提到的概率形状先验项两部分损失函数相加,再进行反向传播更新模型。
$$\min_{z} \frac{1}{2}||x-\hat{x}(z)||^2 + \lambda p(z)$$
其中,$x$为输入图像,$\hat{x}(z)$为深度自编码器输出的潜在编码向量对应的重建图像,$p(z)$为形状先验项,$\lambda$为权重系数。
姿态参数,除了输出一个3D物体形状的点云表示外,本模型还可以输出一个姿态参数,用于描述3D物体在空间中的位置和方向。具体该姿态参数公式表示如下:
$$\theta = [\theta_x, \theta_y, \theta_z, t_x, t_y, t_z]$$
其中,$\theta_x$、$\theta_y$、$\theta_z$分别表示绕$x$、$y$、$z$轴旋转的角度,$(t_x,t_y,t_z)$表示3D物体在空间中的平移向量。
$\mathcal{3.3} \space 网格$
本部分选取了$Wang$$[11]$的Pixel2Mesh模型、$Hu$$[12]$的SMR模型进行介绍。
$\mathcal{3.3.1} \space Pixel2Mesh$
本文提出了一种全新的端到端深度学习架构,可以从单个RGB图像中生成三角形网格的3D形状。该方法使用了基于图的卷积神经网络来表示3D网格,并通过逐步变形椭球来产生正确的几何形状。此外,作者还设计了一个投影层,将感知图像特征融入到GCN所表示的3D几何中,并采用粗到细的方式预测3D几何。整体框架如下图所示。
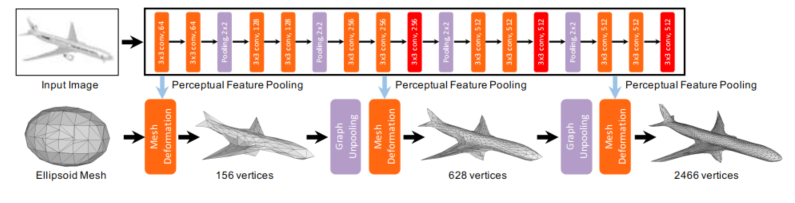
对于一张给定的输入图像,Pixel2Mesh初始化一个固定大小的椭球体作为其初始的形状,整个网络分为上下两个部分,上部分使用CNN做图像的特征提取,下部分是一个级联网格变形。
上下两部分之间连接的部分是Perceptual Feature Pooling,它被用于将图像中提取出来特征与3D网格特征结合起来。在上部分CNN网络的conv3_3、conv4_3和conv5_3层之后,Perceptual Feature Pooling将每个顶点的3D坐标投影到输入图像平面上,并使用双线性插值从四个相邻像素中汇聚特征,从而形成感知特征。然后将每一个形成的感知特征拼接起来形成一个总维度为1280的总感知特征。这个1280维的感知特征又会与输入网格的128维3D特征连接起来,形成一个总维度为1408的特征向量。最后这个向量会被输入到一个全连接层中,以生成每个顶点的3D坐标传输给下部分网络。
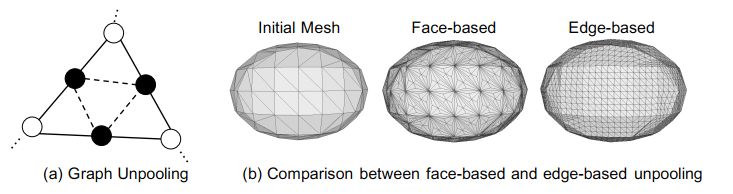
在下部分级联网格变形网络中,Pixel2Mesh使用了三个变形块来逐步将椭球体网格变形为所需的3D模型。每个变形块包含一个GCN模块和一个Graph Unpooling。GCN模块用于学习每个顶点之间的关系,并更新每个顶点的位置。Graph Unpooling用于将当前椭球体网格分解为更精细的子网格、增加GCN的顶点数,并将子网格之间的关系表示为图结构。下图(a)展示了Graph Unpooling添加黑色顶点和虚线边。而Graph Unpooling层有两种实现方式:Face-based和Edge-based。
- Face-based方法是一种直接将新顶点添加到三角形面中心的方法,然后连接它与三角形面上的三个顶点。这种方法简单易行,但会导致不平衡的顶点度数,即每个顶点连接的边数不同。
- 为了解决上述问题,Pixel2Mesh采用了Edge-based方法。Edge-based方法是一种类似于网格细分算法中使用的策略,它在每条边上添加一个新顶点,并将其连接到该边两端的现有顶点。新添加的顶点特征被设置为其两个邻居特征值的平均值。如下图(b)所示,Face-based会导致不平衡的顶点度数,而edge-basd的则保持规则。
$\mathcal{3.3.2} \space SMR$
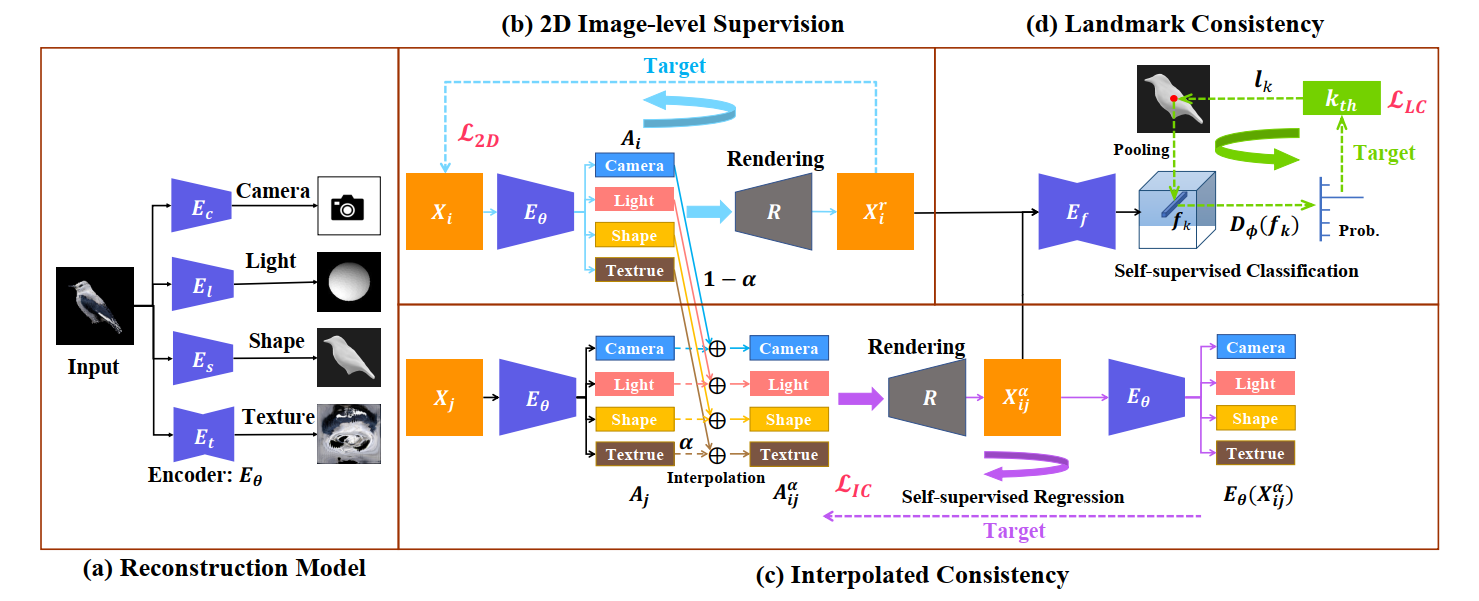
本文提出了一种名为“自监督三维网格重建”(Self-supervised Mesh Reconstruction)的方法,实现从单个图像中重建特定类别的三维网格对象,仅使用轮廓掩码注释。即在训练的过程中不需要3D ground truth,只使用2D标注,就能实现三维重建并且可以推广到不同类别的自然对象。下图展示了SMR的整体框架。
SMR通过属性编码器预测相机、形状、纹理和光等3D属性,并在2D图像和3D网格级别上进行监督。属性编码器采用了一种基于卷积神经网络的结构,包括多个卷积层和池化层。该网络由一个共享的特征提取器和四个分支组成,每个分支对应一个3D属性且每个分支都包括两个全连接层和一个softmax层或一个线性层。其损失函数由两部分组成:分类损失和回归损失。分类损失用于预测相机、形状和纹理等离散变量,而回归损失用于预测光等连续变量。分类损失使用交叉熵损失函数,而回归损失使用均方误差损失函数。在训练过程中,使用自监督回归来优化属性编码器,并使用插补一致性和关键点一致性来提高重建精度。
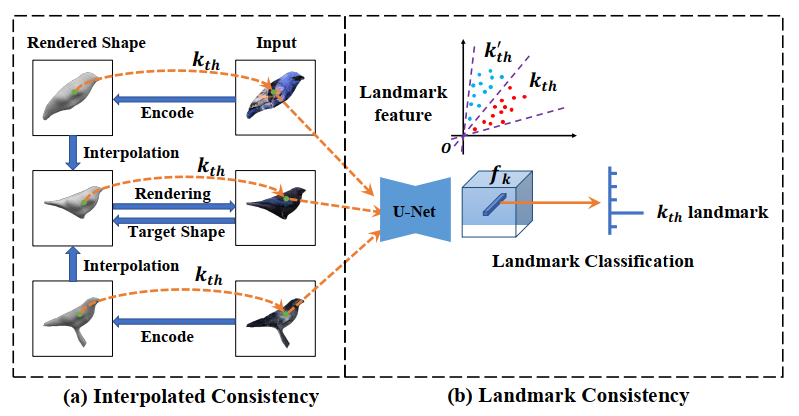
对于自监督学习:在2D层面,SMR使用单个2D图像作为输入,并使用渲染引擎将其转换为3D模型。然后将这个3D模型渲染回多个视角下的2D图像,并将这些图像作为标注用于自监督训练。在训练过程中,使用前面提到的多任务损失函数计算预测值与真实值之间的误差,并使用反向传播算法更新模型参数。在3D层面,SMR使用插补一致性(Interpolated Consistency)和关键点一致性(Landmark Consistency)两种方法来优化3D属性。具体细节过程如下图所示。
- 插补一致性是指在模型将2D图像转为3D模型后的步骤里,随机选择两个不同的3D模型,计算它们之间的距离,然后在这两个3D模型之间进行线性插值,从而生成一个新的3D模型,并将其作为标注用于自监督训练。
- 关键点一致性是指使用重建后的3D网格模型中的点作为关键点,并对每个关键点的特征进行分类。在分类操作中,SMR将每个关键点周围的3D坐标和法向量作为输入,并使用一个分类器对其进行分类。然后将预测值与真实值之间的误差作为损失函数,并使用反向传播算法更新模型参数。
$\mathcal{4} \space 比较与优缺点$
$\mathcal{4.1} \space 输出格式比较$
在章节$2.2$我们介绍了本文的分类方法,分别有体素、点云、网格三种输出格式。本小节将对这三种输出格式进行比较,分析它们各自的优缺点。
体素表示法的每个立方体单元可以存储各种属性,如密度、颜色和纹理等。其优点是能够捕捉物体的内部结构,同时在进行几何操作时,也能够更快地进行计算;同时它的表示形式也具有较好的可扩展性和可压缩性,可以轻松地进行模型的变形和编辑。但由于体素的大小是固定的,对于复杂的模型,需要使用更小的体素才能保证模型的精度,这会增加计算量和内存消耗且需要离散化三维空间,占用大量的内存空间;同时它不能很好地表达曲面的细节,尤其是对于光滑的曲面。
点云表示法不需要像体素一样将空间进行离散化,而是直接表示三维模型的表面,因此它可以表达模型的细节和曲面形状。同时在数据结构内部,可以使用较为稀疏的方式来表示大规模的点云,节约了内存空间,存储效率高。但也正是因为这种存储的不连续性,计算体积等问题就会变得很复杂。与体素相比,点云无法捕捉表面的纹理和光照信息,且对于不规则形状的物体,点云表示形式的精度可能会受到影响。同时由于点云数据之间的匹配和对应关系需要通过复杂的算法求解,因此点云处理的计算复杂度较高。
网格表示法最大的优点是其具有很好的通用性,很多三维软件都可以读取和处理网格数据。由于网格是由一系列连接的三角形组成的,因此可以很好地捕捉到物体表面的细节信息,从而准确地表示物体表面的形状和曲率信息;同时图形卡可以很高效地渲染三角形,因此网格可以被很容易地可视化。但由于需要存储大量的三角形,网格表示法会占用大量的存储空间,在处理大规模数据时,往往需要进行压缩和优化,以减小数据量和提高渲染效率。
$\mathcal{4.2} \space 各模型优缺点分析$
$\mathcal{4.2.1} \space 体素$
$3D-R2N2$
优点(1)该模型使用了LSTM循环神经网络来处理输入图像序列,能够捕捉输入图像之间的时序关系,从而提高了重建性能;(2)使用了渐进式增强的技术来逐步增加输入图像分辨率和输出网格分辨率,有助于提高网络性能并减少过拟合现象;(3)可以处理多个物体实例,并且能够在不同物体实例之间共享参数,从而减少模型复杂度。
缺点(1)由于使用的输出格式是体素,模型需要大量的计算资源和时间来训练和测试,因此需要强大的计算机硬件支持;(2)对于大规模数据集的训练需要较长时间,并且需要大量的存储空间;(3)更重要的是,该模型对于不同类别的物体需要单独进行训练,因此需要针对每个类别收集足够数量和质量的数据;(4)同时,模型对于输入图像数量和视角数量有一定限制,如果输入图像数量或视角数量过少,可能会影响重建结果;(5)如果物体形状过于复杂,可能也会影响重建结果。
$DeepSDF$
优点(1)与传统的基于网格的方法相比,本模型可以更好地处理不规则形状和空洞等问题;(2)生成的几何形状具有较高的精度和细节,可以用于各种应用场景;(3)可以通过学习潜在空间来实现形状插值和形状变换等操作,具有较强的可扩展性。
缺点(1)模型对数据集中存在的噪声和偏差比较敏感,可能会导致生成结果出现一些不合理或异常情况;(2)拥有体素输出表达方式的通病,需要大量的计算资源和时间来训练和测试,因此需要强大的计算机硬件支持;(3)对于大规模数据集的训练需要较长时间,并且需要大量的存储空间。
$BodyNet$
优点(1)可以从单张RGB图像中预测出人体的三维形状,具有很好的性能和鲁棒性;(2)采用了特征融合和级联的方式将各个子网络联合起来,并且通过多任务学习来共享特征和传递信息,提高了模型的性能和泛化能力,并且减少训练时间和计算资源消耗。
缺点(1)在处理非常复杂或极端情况下(如遮挡、姿态变化、光照变化等)可能存在一定程度上的误差或不稳定性;(2)只能处理单视角输入的图,可能会存在camera ambiguity的问题,导致重建结果不正确。
$\mathcal{4.2.2} \space 点云$
$Using \space Deformation \space Vector \space Fields$
优点(1)采用了深度图作为中间表示,可以有效地减少点云重建过程中的计算量;(2)可以处理多视角输入,提高了点云重建的精度和鲁棒性;(3)采用了组合损失函数,包括了单视角损失、多视角一致性损失和正则化项,可以更好地平衡不同损失之间的权重,从而提高了模型的性能。
缺点(1)对输入数据要求较高,由于模型采用了深度图作为中间表示,因此需要输入数据中包含深度信息。如果输入数据中没有深度信息,则需要使用其他方法来获取深度信息,这可能会增加额外的计算量和复杂性。(2)由于采用了点云重建方法,因此对噪声和遮挡比较敏感。如果输入数据中存在大量噪声或者遮挡比较严重,可能会导致点云重建的精度下降。因此,可能需要考虑对输入数据进行预处理,以减少噪声和遮挡的影响。(3)模型主要针对单个物体的点云重建,对于复杂场景或多个物体的点云重建可能存在一定的局限性。
$Based \space on \space Unsupervised \space Learning$
优点(1)不需要使用任何标注数据进行训练,因此可以在没有大量标注数据的情况下进行训练,适用于更广泛的场景和应用;(2)可以从两张RGB图像中预测物体的3D形状和相机姿态,并将它们转换为图像进行比较和训练,解决了camera ambiguity的问题。
缺点(1)模型使用了复杂的CNN模型和集成学习方法,因此训练时间比较长。在实验中,作者使用了多个GPU进行训练,但训练时间仍需要数周,这使得该模型在实际应用中可能不太适用于需要快速响应的场景。(2)由于该模型是从单张RGB图像中预测物体的3D形状和相机姿态,因此它对光照和背景比较敏感。如果输入图像的光照或背景发生变化,可能会导致预测结果不准确。
$Using \space Deep \space Shape \space Prior \space and \space Silhouette$
优点(1)引入形状先验,提出了一种基于高斯分布的形状先验,用于约束3D物体形状的重建过程。通过在线学习形状先验的方法,可以更好地适应不同的物体形状,并得到更准确、稳定的3D物体重建结果。(2)在优化过程中考虑了概率分布,将重建误差和形状先验项两部分损失函数相加,并使用随机梯度下降算法来最小化这个总的损失函数,这样可以使得优化过程更加稳定和准确,并且能够更好地适应不同的物体形状。(3)除了输出一个3D物体形状的点云表示外,模型还可以输出一个姿态参数,用于描述3D物体在空间中的位置和方向,这样可以更好地理解和使用重建结果。(4)实验结果表明,模型能够在保持高质量重建结果的同时,具有更快的运行速度和更好的鲁棒性,表现优异。
缺点(1)依赖于深度自编码器,由于使用了基于卷积神经网络的深度自编码器来学习3D物体形状的潜在表示,因此需要大量的标注数据来训练深度自编码器,否则可能会导致模型性能下降;(2)模型需要输入一张包含物体轮廓信息的图像,因此对输入图像的质量和准确性要求较高,如果输入图像中物体轮廓信息不清晰或者存在噪声,可能会导致重建结果不准确;(3)只能处理单个物体的重建,无法处理多个物体或者复杂场景中的3D重建问题。
$\mathcal{4.2.3} \space 网格$
$Pixel2Mersh$
优点(1)可以从单张图像中生成真实且精确的三维模型,无需使用多个视角或深度信息;(2)可以处理各种形状和姿态的物体,并且对输入图像中物体表面的纹理和形状信息进行了更好的捕捉;(3)使用了一种新颖的感知特征汇聚技术,将图像特征和3D网格特征结合起来,以便更好地生成真实且精确的三维模型。
缺点(1)本模型是基于单张图像生成三维模型,因此对于复杂场景或物体,其性能可能会受到限制;(2)若输入的图像质量低、有物体遮挡或含有噪声,可能会产生不准确或不完整的三维模型。
$SMR$
优点(1)可以使用单个2D图像作为输入,并使用渲染引擎将其转换为3D模型,因此可以在不需要3D ground truth注释的情况下进行训练,并且可以推广到不同类别的自然对象;(2)使用多任务损失函数计算预测值与真实值之间的误差,并使用反向传播算法更新模型参数,通过这种方式,可以同时优化2D和3D层面的监督,并提高重建精度;(3)使用插补一致性和关键点一致性两种自监督方法来优化3D属性,可以保证每个小部分都有更好的建模效果,并提高重建精度。
缺点(1)难以处理非刚性物体等具有更复杂的形状和姿态变化。
$\mathcal{4.3} \space 比较与总结$
下表对本文介绍的八个模型进行了对比。其中:“多输入”代表模型输入的图像/三维图形的数目;“对输入数据要求”代表输入的图像质量、是否有物体遮挡或含有噪声是否会对模型造成较大影响,越高代表影响越大;“重建物体复杂度”里“一般”代表只能重建单一物体或简单场景物体,“高”代表可以重建多个物体或复杂场景;“姿势歧义”里程度越高代表姿势歧义问题越严重。
| 模型 | 多输入 | 监督类型 | 内存消耗 | 对输入数据要求 | 重建物体复杂度 | 姿势歧义问题 |
|---|---|---|---|---|---|---|
| 3D-R2N2 | 是 | 监督学习 | 高 | 一般 | 一般 | 低 |
| DeepSDF | 否 | 监督学习 | 高 | 一般 | 高 | 一般 |
| BodyNet | 否 | 监督学习 | 高 | 一般 | 高 | 严重 |
| Using Deformation Vector Fields | 否 | 监督学习 | 一般 | 高 | 一般 | 一般 |
| Based on Unsupervised Learning | 是 | 无监督学习 | 一般 | 高 | 高 | 低 |
| Using Deep Shape Prior and Silhouette | 否 | 监督学习 | 一般 | 高 | 一般 | 低 |
| Pixel2Mersh | 否 | 监督学习 | 一般 | 高 | 一般 | 一般 |
| SMR | 否 | 无监督学习 | 一般 | 一般 | 一般 | 一般 |
由上表可知,大部分模型只能解决单一或简单的图像重建问题,而哪怕可以对复杂场景或多个物体进行三维重建,也会对输入的图像要求较高,容易受到强光、噪声或遮挡物的干扰。同时,许多模型还是使用监督学习的方法,这种方法就需要对训练数据三维方面进行标注,需要很大的成本。姿势歧义的问题也有待进一步解决。
$\mathcal{5} \space 未来与展望$
未来,深度学习技术在三维重建领域将继续发挥重要作用。随着硬件的发展和算法的优化,三维重建技术的效率和精度将不断提高。以下是可能的趋势:
(1)更加精确的3D重建:未来的研究将致力于提高图像3D重建的精度和准确性,这可能涉及到更复杂的模型和算法,以及更多的训练数据;
(2)更广泛的应用场景:三维重建技术将被应用于更广泛的领域,例如虚拟现实、增强现实、医学影像等,这将需要更多的研究来适应不同领域的需求;
(3)更高效的重建算法:未来的研究将致力于开发更高效、更快速、更可扩展的算法,以便在处理大规模数据集时能够提供更好的性能。
$\mathcal{6} \space 参考文献$
- Laurentini, Aldo. “The visual hull concept for silhouette-based image understanding.” IEEE Transactions on pattern analysis and machine intelligence 16.2 (1994): 150-162.
- Hartley, Richard, and Andrew Zisserman. Multiple view geometry in computer vision. Cambridge university press, 2003.
- Han, Xian-Feng, Hamid Laga, and Mohammed Bennamoun. “Image-based 3D object reconstruction: State-of-the-art and trends in the deep learning era.” IEEE transactions on pattern analysis and machine intelligence 43.5 (2019): 1578-1604.
- Choy, Christopher B., et al. “3d-r2n2: A unified approach for single and multi-view 3d object reconstruction.” Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, October 11-14, 2016, Proceedings, Part VIII 14. Springer International Publishing, 2016.
- Park, Jeong Joon, et al. “DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation.” Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2019.
- Varol, Gul, et al. “Bodynet: Volumetric inference of 3d human body shapes.” Proceedings of the European conference on computer vision (ECCV). 2018.
- David Eigen, Christian Puhrsch, and Rob Fergus, “Depth Map Prediction From a Single Image Using a Multi-scale Deep Network,” Advances in neural information processing systems 27 (2014).
- Li, Kejie, et al. “Efficient dense point cloud object reconstruction using deformation vector fields.” Proceedings of the European Conference on Computer Vision (ECCV). 2018.
- Insafutdinov, Eldar, and Alexey Dosovitskiy. “Unsupervised learning of shape and pose with differentiable point clouds.” Advances in neural information processing systems 31 (2018).
- Li, Kejie, et al. “Single-view object shape reconstruction using deep shape prior and silhouette.” arXiv preprint arXiv:1811.11921 (2018).
- Wang, Nanyang, et al. “Pixel2mesh: Generating 3d mesh models from single rgb images.” Proceedings of the European conference on computer vision (ECCV). 2018.
- Hu, Tao, et al. “Self-supervised 3D mesh reconstruction from single images.” Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2021.
$\mathcal{7} \space 查重结果$
