二周目复习版本 : )
PS: 一年多之后再看这篇突然觉得学计算机真好啊!!
时序模型
RNN
基本介绍
RNN 的基本单元结构如下图所示:
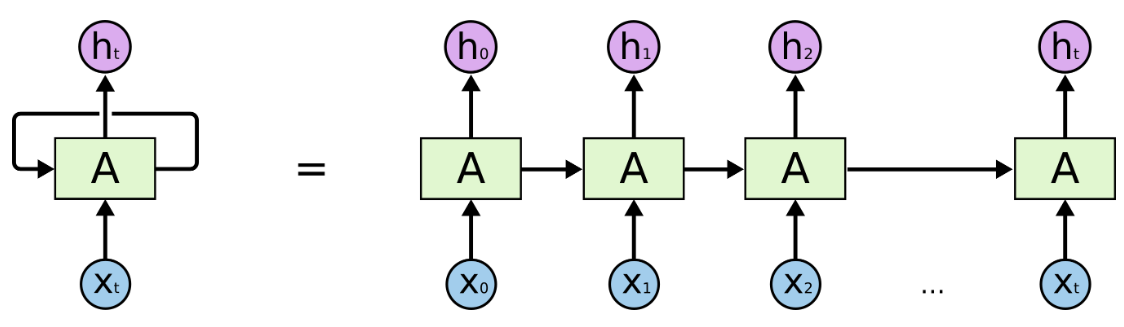
上图左边部分称作 RNN 的一个 timestep,在这个 timestep 中可以看到,在 $t$ 时刻,输入变量 $x_t$,通过 RNN 的一个基础模块 A,输出变量 $h_t$,而 $t$ 时刻的信息,将会传递到下一个时刻 $t+1$。
如果把模块按照时序展开,则会如上图右边部分所示,由此可以看到 RNN 为多个基础模块 A 的互连,每一个模块都会把当前信息传递给下一个模块。
RNN 解决了时序依赖问题,但这里的时序一般指的是短距离的,首先我们先介绍下短距离依赖和长距离依赖的区别:
- 短距离依赖:对于这个填空题 “我想看一场篮球____”,我们很容易就判断出 “篮球” 后面跟的是 “比赛”,这种短距离依赖问题非常适合 RNN。
- 长距离依赖:对于这个填空题 “我出生在中国的瓷都景德镇,小学和中学离家都很近,……,我的母语是____”,对于短距离依赖,“我的母语是” 后面可以紧跟着 “汉语”、“英语”、“法语”,但是如果我们想精确答案,则必须回到上文中很长距离之前的表述 “我出生在中国的瓷都景德镇”,进而判断答案为 “汉语”,而 RNN 是很难学习到这些信息的。
梯度消失问题
为什么RNN不适合长距离依赖问题
RNN前向传播过程:
- 隐藏状态:$h ^{(t)} = \sigma (z ^{(t)}) = \sigma(Ux ^{(t)} + Wh ^{(t-1)} + b)$ ,此处激活函数一般为 $tanh$ 。
- 模型输出:$o ^{(t)} = Vh ^{(t)} + c$
- 预测输出:$\hat{y} ^{(t)} = \sigma(o ^{(t)})$,此处激活函数一般为$softmax$。
- 模型损失:$L = \sum _{t = 1} ^{T} L ^{(t)}$
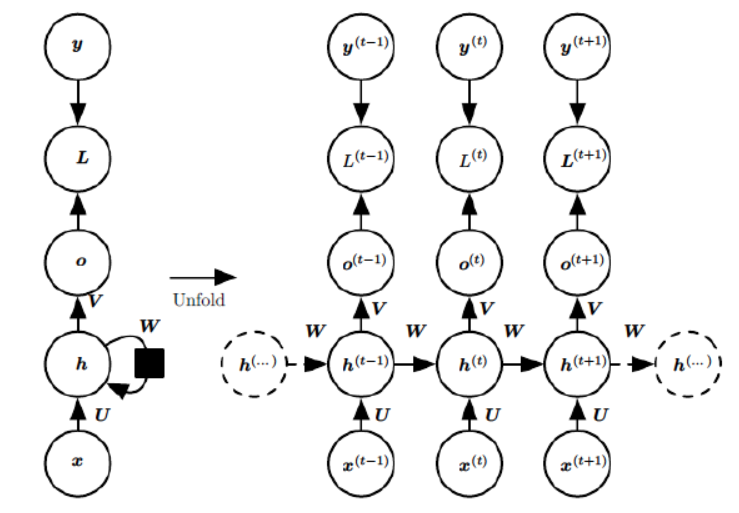
RNN 所有的 timestep 共享一套参数 $U,V,W$,在 RNN 反向传播过程中,需要计算 $U,V,W$等参数的梯度,以 $W$ 的梯度表达式为例(假设 RNN 模型的损失函数为 $L$):
$$\frac{\partial L}{\partial W}
= \sum_{t = 1}^{T} \frac{\partial L}{\partial y^{(T)}} \frac{\partial y^{(T)}}{\partial o^{(T)}} \frac{\partial o^{(T)}}{\partial h^{(T)}} \left( \prod_{k=t + 1}^{T} \frac{\partial h^{(k)}}{\partial h^{(k - 1)}} \right) \frac{\partial h^{(t)}}{\partial W} \ $$
$$= \sum_{t = 1}^{T} \frac{\partial L}{\partial y^{(T)}} \frac{\partial y^{(T)}}{\partial o^{(T)}} \frac{\partial o^{(T)}}{\partial h^{(T)}} \left( \prod_{k=t+1}^{T} tanh^{‘}(z^{(k)}) W \right) \frac{\partial h^{(t)}}{\partial W}$$
公式中$\left( \prod_{k=t + 1}^{T} \frac{\partial h^{(k)}}{\partial h^{(k - 1)}} \right) = \left( \prod_{k=t+1}^{T} tanh^{‘}(z^{(k)}) W \right)$,$tanh$的导数总是小于 1 的,由于是 $T−(t+1)$ 个 timestep 参数的连乘,如果 $W$ 的主特征值小于 1,梯度便会消失;如果 $W$ 的特征值大于 1,梯度便会爆炸。
RNN中权重在各时间步内共享,最终的梯度是各个时间步的梯度和,梯度和会越来越大。因此,RNN中总的梯度是不会消失的,即使梯度越传越弱,也只是远距离的梯度消失。 RNN所谓梯度消失的真正含义是,梯度被近距离(t+1趋向于T)梯度主导,远距离(t+1远离T)梯度很小,导致模型难以学到远距离的信息。
LSTM
为了解决 RNN 缺乏的序列长距离依赖问题,LSTM 被提了出来
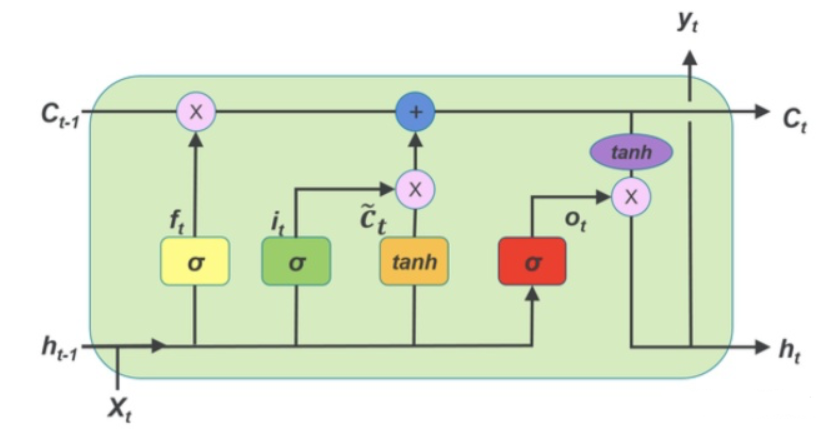
如上图所示,为 LSTM 的 RNN 门控结构(LSTM 的 timestep),LSTM 前向传播过程包括:
- 遗忘门:决定了丢弃哪些信息,遗忘门接收 $t−1$ 时刻的状态 $h _t−1$,以及当前的输入 $x _t$,经过 Sigmoid 函数后输出一个 0 到 1 之间的值 $f_t$
- 输出:$f_{t} = \sigma(W_fh_{t-1} + U_f x_{t} + b_f)$
- 输入门:决定了哪些新信息被保留,并更新细胞状态,输入们的取值由 $h_t−1$ 和 $x_t$ 决定,通过 Sigmoid 函数得到一个 0 到 1 之间的值 $i_t$,而 $tanh$ 函数则创造了一个当前细胞状态的候选 $a_t$
- 输出:$i_{t} = \sigma(W_ih_{t-1} + U_ix_{t} + b_i)$,$\tilde{C_{t} }= tanh(W_ah_{t-1} + U_ax_{t} + b_a)$
- 细胞状态:旧细胞状态 $C_t−1$ 被更新到新的细胞状态 $C_t$ 上,
- 输出:$C_{t} = C_{t-1}\odot f_{t} + i_{t}\odot \tilde{C_{t} }$
- 输出门:决定了最后输出的信息,输出门取值由 $h_t−1$ 和 $x_t$ 决定,通过 Sigmoid 函数得到一个 0 到 1 之间的值 $o_t$,最后通过 $tanh$ 函数决定最后输出的信息
- 输出:$o_{t} = \sigma(W_oh_{t-1} + U_ox_{t} + b_o)$,$h_{t} = o_{t}\odot tanh(C_{t})$
- 预测输出:$\hat{y} _{t} = \sigma(Vh _{t}+c)$
LSTM 遗忘门值 $f_t$ 可以选择在 [0,1] 之间,让 LSTM 来改善梯度消失的情况。也可以选择接近 1,让遗忘门饱和,此时远距离信息梯度不消失;也可以选择接近 0,此时模型是故意阻断梯度流,遗忘之前信息。
另外需要强调的是LSTM搞的这么复杂,除了在结构上天然地克服了梯度消失的问题,更重要的是具有更多的参数来控制模型;通过四倍于RNN的参数量,可以更加精细地预测时间序列变量。
Attention
本质思想:从大量信息中有选择地筛选出少量重要信息并聚焦到这些重要信息上,忽略不重要的信息。
Attention 机制可以更加好的解决序列长距离依赖问题,并且具有并行计算能力。
基本思想
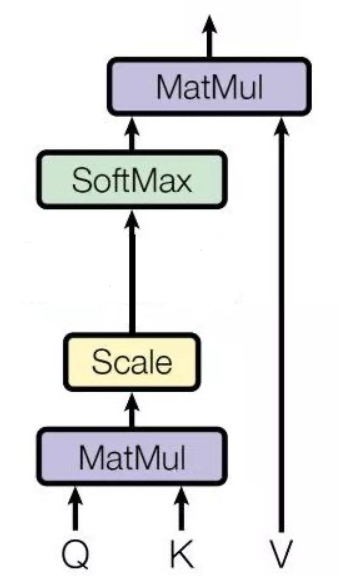
通过 Query 这个信息从 Values 中筛选出重要信息,简单点说,就是计算 Query 和 Values 中每个信息的相关程度。
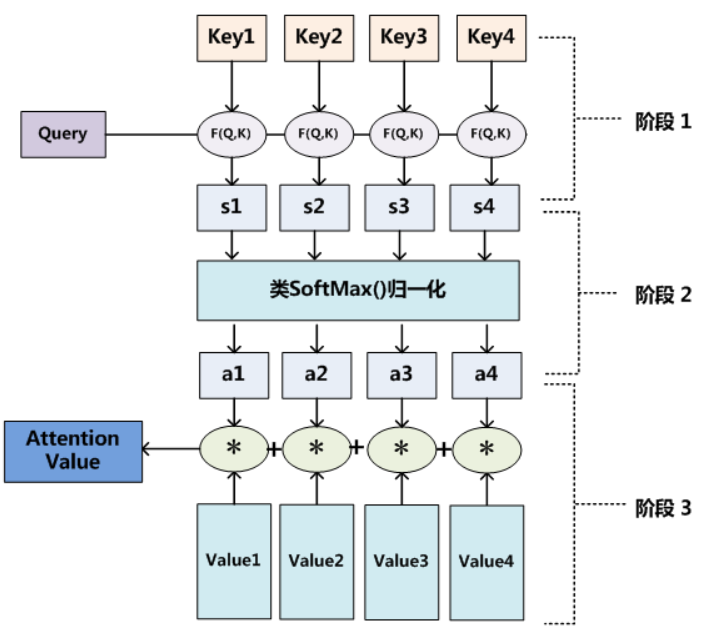
如上图,将 Query(Q) 和 key-value pairs(把 Values 拆分成了键值对的形式) 映射到输出上,其中 query、每个 key、每个 value 都是向量,输出是 V 中所有 values 的加权,其中权重是由 Query 和每个 key 计算出来的,计算方法分为三步:
- 计算比较 Q 和 K 的相似度,用 f 来表示:$f(Q,K_i)$,$i=1,2,⋯,m$,一般第一步计算方法包括四种
- 点乘(Transformer 使用):$f(Q,K_i) = Q^T K_i$
- 权重:$f(Q,K_i) = Q^TWK_i$
- 拼接权重:$f(Q,K_i) = W[Q^T;K_i]$
- 感知器:$f(Q,K_i)=V^T \tanh(WQ+UK_i)$
- 将得到的相似度进行 softmax 操作,进行归一化,$\alpha_i = softmax(\frac{f(Q,K_i)}{\sqrt{d_k}})$
- 除以$\sqrt{d_k}$的作用:假设 $Q$, $K$ 里的元素的均值为0,方差为 1,那么 $A^T=Q^TK$ 中元素的均值为 0,方差为 d。当 d 变得很大时, $A$ 中的元素的方差也会变得很大,如果 $A$ 中的元素方差很大(分布的方差大,分布集中在绝对值大的区域),在数量级较大时, softmax 将几乎全部的概率分布都分配给了最大值对应的标签,由于某一维度的数量级较大,进而会导致 softmax 未来求梯度时会消失。总结一下就是 $softmax(A)$ 的分布会和d有关。因此 $A$ 中每一个元素乘上 $\frac{1}{\sqrt{d_k}}$ 后,方差又变为 1,并且 $A$ 的数量级也将会变小。
- 针对计算出来的权重$\alpha _i$,对 $V$ 中的所有 values 进行加权求和计算,得到 Attention 向量:$Attention = \sum _{i=1}^m \alpha _i V_i$
Self Attention
基本架构
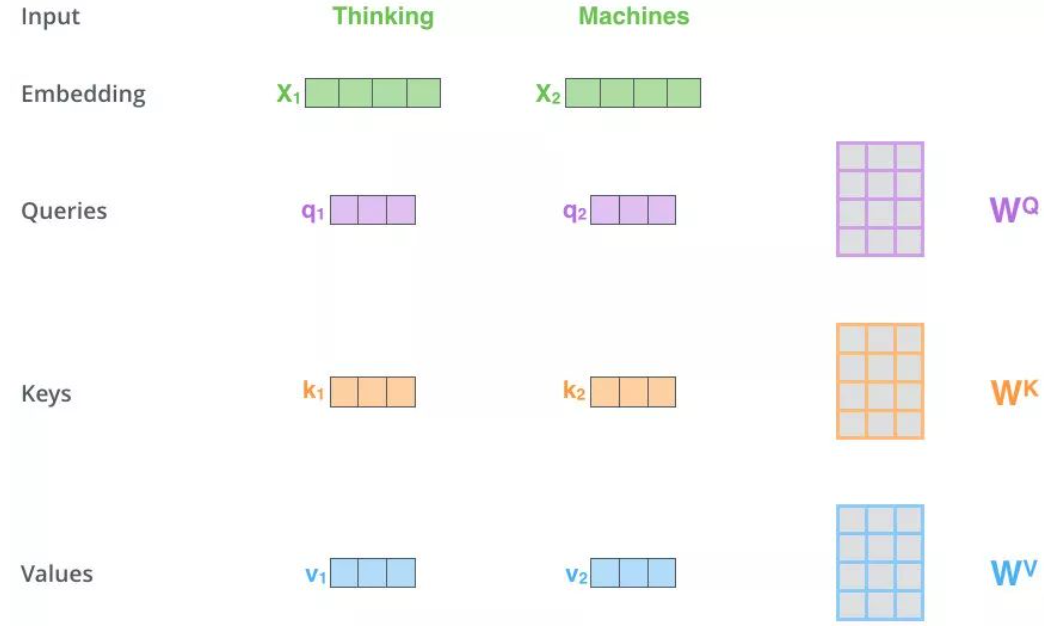
对于 Self Attention,Q、K、V 来自句子 X 的 词向量 x 的线性转化,即对于词向量 x,给定三个可学习的矩阵参数 $W_Q$,$W_k$,$W_v$,x 分别右乘上述矩阵得到 Q、K、V。
向量计算过程
Q、K、V的获取:两个单词 Thinking 和 Machines。通过线性变换,即 $x_1$ 和 $x_2$ 两个向量分别与$W_q$, $W_k$, $W_v$ 三个矩阵点乘得到 $q_1$, $q_2$, $k_1 $, $k_2$, $v_1$, $v_2$ 共 6 个向量。矩阵 Q 则是向量 $q_1$, $q_2$ 的拼接,K、V 同理。
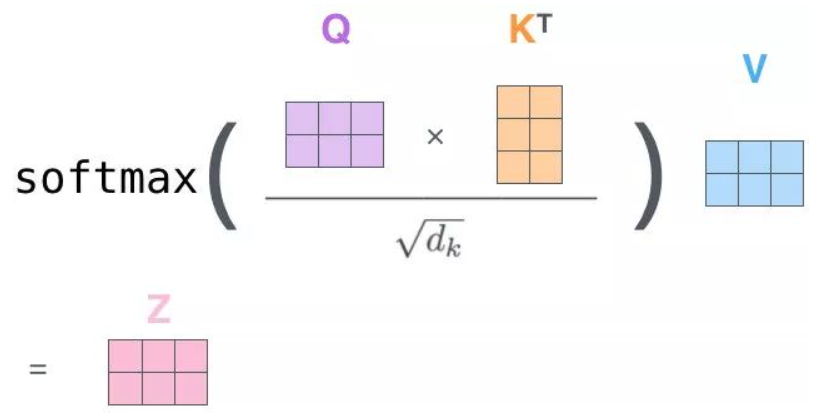
MatMual:向量 q1,k1做点乘得到得分 112, q1,k2做点乘得到得分96。注意:这里是通过 q1 这个信息找到 x1,x2 中的重要信息。
Scale + Sofatmax
MatMul:乘上V。用得分比例 [0.88,0.12] 乘以 [v1,v2] 值得到一个加权后的值,将这些值加起来得到 z1。

总结过程:用 $q_1$、$K=[k1,k2]$ 去计算一个 Thinking 相对于 Thinking 和 Machine 的权重,再用权重乘以 Thinking 和 Machine 的 $V=[v_1,v_2]$ 得到加权后的 Thinking 和 Machine 的 $V=[v_1,v_2]$,最后求和得到针对各单词的输出 $z_1$。同理可以计算出 Machine 相对于 Thinking 和 Machine 的加权输出 $z_2$,拼接 $z_1$ 和 $z_2$ 即可得到 Attention 值 $Z=[z_1,z_2]$
矩阵计算过程
$QK^T$ 其实就会组成一个 word2word 的 attention map!(加了 softmax 之后就是一个合为 1 的权重了)。比如说你的输入是一句话 “i have a dream” 总共 4 个单词,这里就会形成一张 4x4 的注意力机制的图:
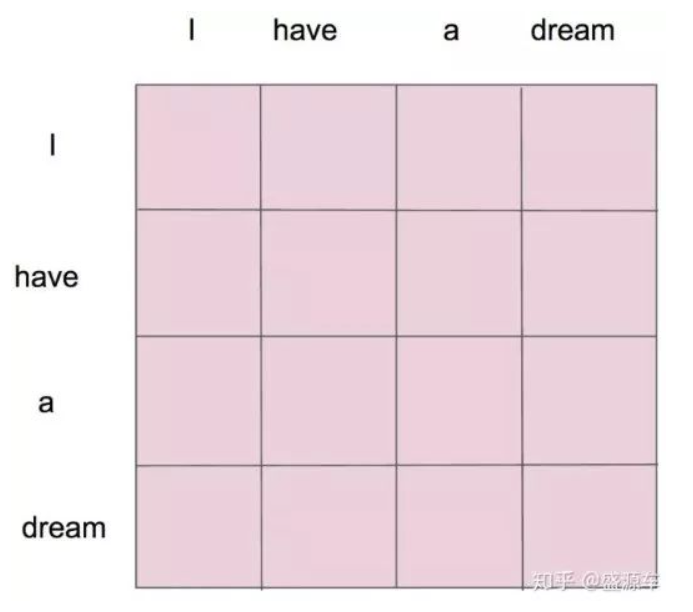
这样一来,每一个单词对应每一个单词都会有一个权重,这也是 Self Attention 名字的来源,即 Attention 的计算来源于 Source(源句) 和 Source 本身,通俗点讲就是 Q、K、V 都来源于输入 X 本身。
与RNN、LSTM的比较
- RNN、LSTM:如果是 RNN 或者 LSTM,需要依次序列计算,对于远距离的相互依赖的特征,要经过若干时间步步骤的信息累积才能将两者联系起来,而距离越远,有效捕获的可能性越小。
- Self Attention:
- 引入 Self Attention 后会更容易捕获句子中长距离的相互依赖的特征,因为 Self Attention 在计算过程中会直接将句子中任意两个单词的联系通过一个计算步骤直接联系起来,所以远距离依赖特征之间的距离被极大缩短,有利于有效地利用这些特征;
- 除此之外,Self Attention 对于一句话中的每个单词都可以单独的进行 Attention 值的计算,也就是说 Self Attention 对计算的并行性也有直接帮助作用,而对于必须得依次序列计算的 RNN 而言,是无法做到并行计算的。
无论句子序列多长,都可以充分捕获近距离上往下问中的任何依赖关系,进而可以很好的提取句法特征还可以提取语义特征;而且对于一个句子而言,每个单词的计算是可以并行处理的。
理论上 Self-Attention (Transformer 50 个左右的单词效果最好)解决了 RNN 模型的长序列依赖问题,但是由于文本长度增加时,训练时间也将会呈指数增长,因此在处理长文本任务时可能不一定比 LSTM(200 个左右的单词效果最好) 等传统的 RNN 模型的效果好。
Masked Self Attention
基本结构如下:
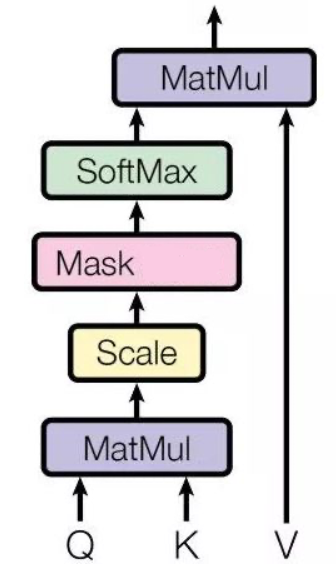
通过 scale 之前的步骤得到一个 attention map,而 mask 就是沿着对角线把灰色的区域用0覆盖掉,不给模型看到未来的信息,如下图所示:
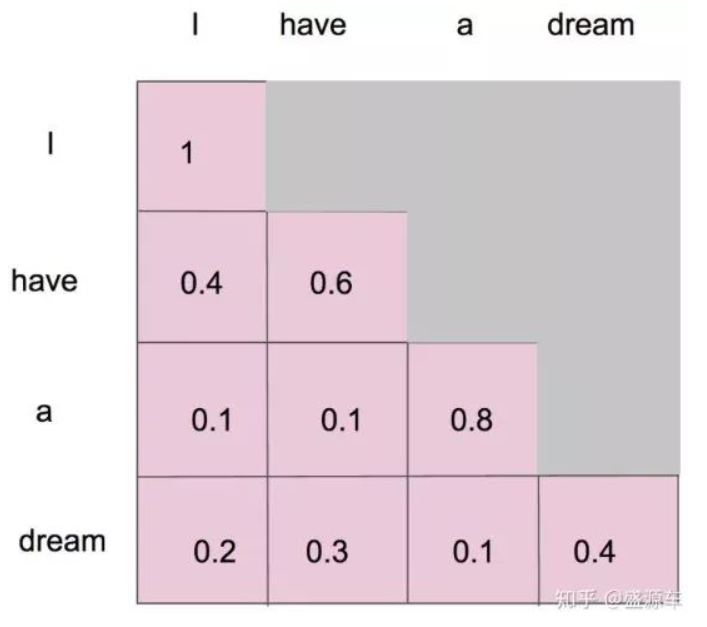
详细来说:
- “i” 作为第一个单词,只能有和 “i” 自己的 attention;
- “have” 作为第二个单词,有和 “i、have” 前面两个单词的 attention;
- “a” 作为第三个单词,有和 “i、have、a” 前面三个单词的 attention;
- “dream” 作为最后一个单词,才有对整个句子 4 个单词的 attention。
并且在做完 softmax 之后,横轴结果合为 1。
Multi-head Self Attention
Multi-Head Attention 就是把 Self Attention 得到的注意力值 $Z$ 切分成 $n$ 个 $Z_1,Z_2,⋯,Z_n$,然后通过全连接层获得新的 $Z′$.
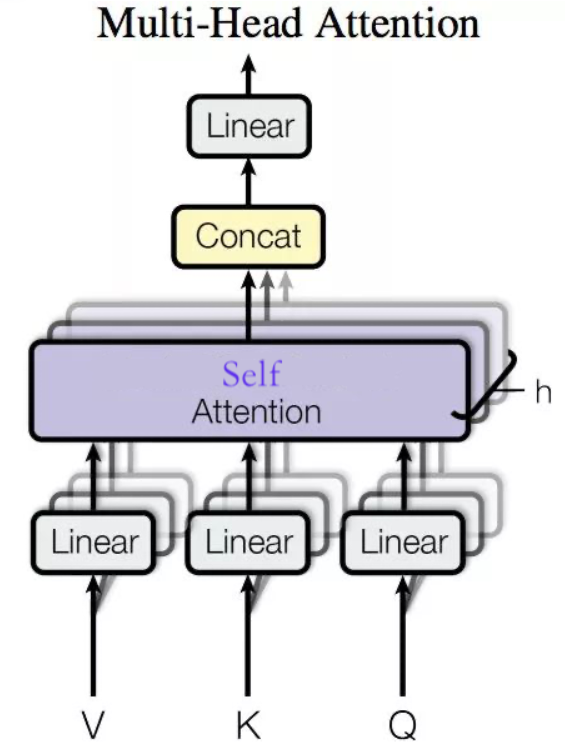
过程如下:
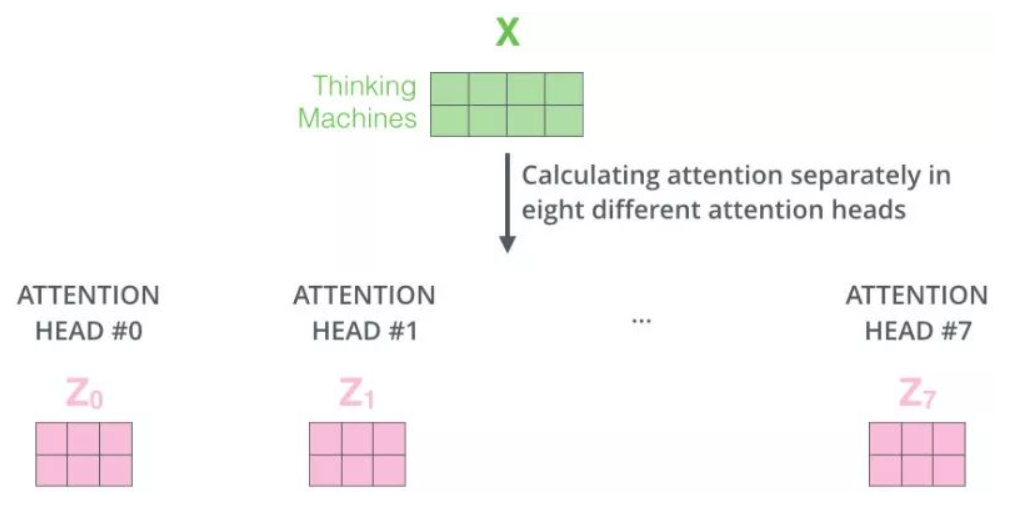
为了使得输出与输入结构相同,拼接矩阵 $Z_i$ 后乘以一个线性 $W_0$ 得到最终的Z

多头相当于把原始信息 Source 放入了多个子空间中,也就是捕捉了多个信息,对于使用 multi-head(多头) attention 的简单回答就是,多头保证了 attention 可以注意到不同子空间的信息,捕捉到更加丰富的特征信息。
Position Embedding
why need position embedding?
Self Attention 的 Q、K、V 三个矩阵是由同一个输入 $X1=(x_1,x_2,⋯,x_n)$线性转换而来,也就是说对于这样的一个被打乱序列顺序的 $X2=(x_2,x_1,⋯,x_n)$ 而言,由于 Attention 值的计算最终会被加权求和,也就是说两者最终计算的 Attention 值都是一样的,进而也就表明了 Attention 丢掉了 $X1$ 的序列顺序信息。
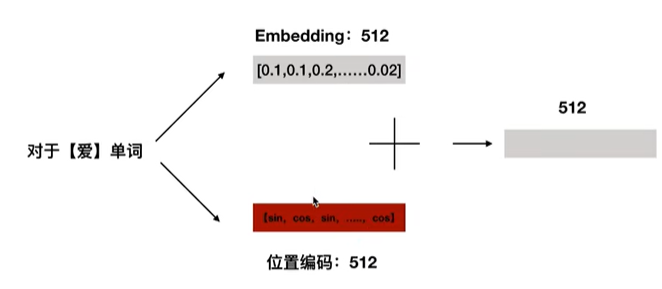
为了解决 Attention 丢失的序列顺序信息,Transformer 作者提出了 Position Embedding,也就是对于输入 $X$ 进行 Attention 计算之前,在 $X$ 的词向量中加上位置信息,也就是说 $X$ 的词向量为$X_{final _embedding}=Embedding+Positional Embedding$
计算方法:
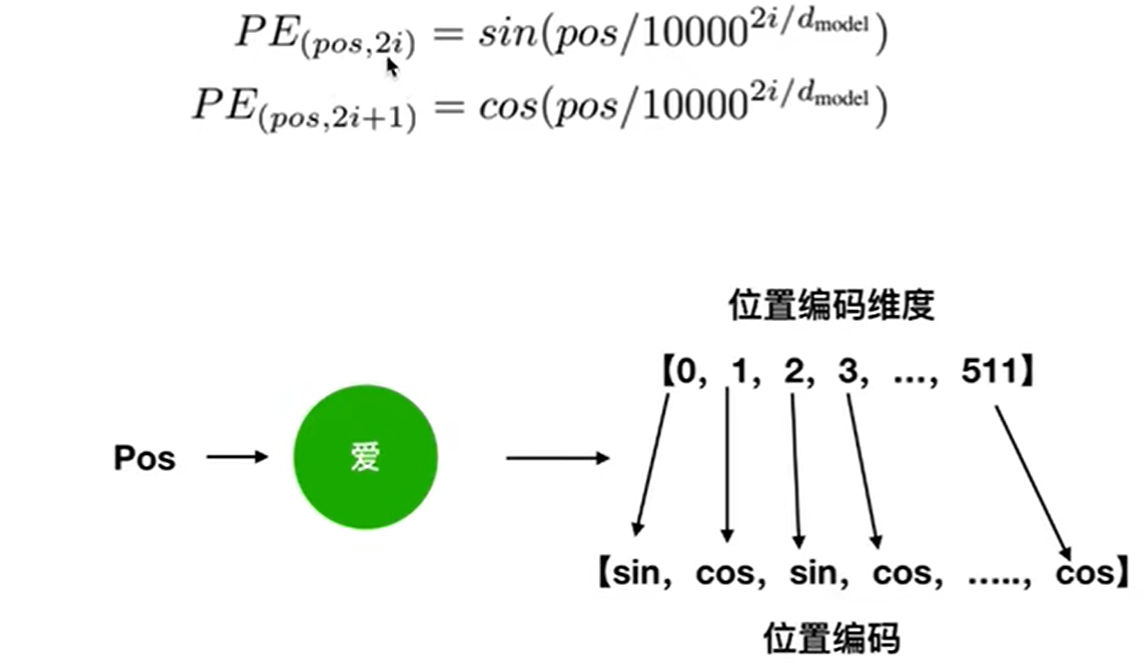
其中 pos 表示位置、i 表示维度、$d_{model}$表示位置向量的向量维度 、$2i$、$2i+1$ 表示的是奇偶数(奇偶维度),上图所示就是偶数位置使用 $sin$ 函数,奇数位置使用 $cos$ 函数。

假设 $pos=1=$我、$k=2=$爱、$pos+k=$3=吃,也就是说 $pos+k=3$ 位置的位置向量的某一维可以通过 $pos=1$ 位置的位置向量的某一维线性组合加以线性表示,通过该线性表示可以得出 “吃” 的位置编码信息蕴含了相对于前两个字 “我” 的位置编码信息。
总而言之就是,某个单词的位置信息是其他单词位置信息的线性组合,这种线性组合就意味着位置向量中蕴含了相对位置信息。
ELMo
很多机器学习任务都需要带标签的数据集作为输入完成。但是我们身边存在大量没有标注的数据,例如文本、图片、代码等等。标注这些数据需要花费大量的人力和时间,标注的速度远远不及数据产生的速度,所以带有标签的数据往往只占有总数据集很小的一部分。随着算力的不断提高,计算机能够处理的数据量逐渐增大。如果不能很好利用这些无标签的数据就显得很浪费。
所以半监督学习和预训练+微调的二阶段模式整变得越来越受欢迎。最常见的二阶段方法就是Word2Vec,使用大量无标记的文本训练出带有一定语义信息的词向量,然后将这些词向量作为下游机器学习任务的输入,就能够大大提高下游模型的泛化能力。
预训练
但是Word2Vec有一个问题,就是单个单词只能有一个Embedding。这样一来,一词多义就不能很好地进行表示。在实际使用 Word Embedding 的时候,单词已经具备了特定的上下文了,这个时候我可以根据上下文单词的语义再去调整单词的 Word Embedding 表示,这样经过调整后的 Word Embedding 更能表达在这个上下文中的具体含义,自然也就解决了多义词的问题了。所以 ELMo 本身是个根据当前上下文对 Word Embedding 动态调整的思路。
ELMo 采用了典型的两阶段过程:
- 第一个阶段是利用语言模型进行预训练;
- 第二个阶段是在做下游任务时,从预训练网络中提取对应单词的网络各层的 Word Embedding 作为新特征补充到下游任务中。
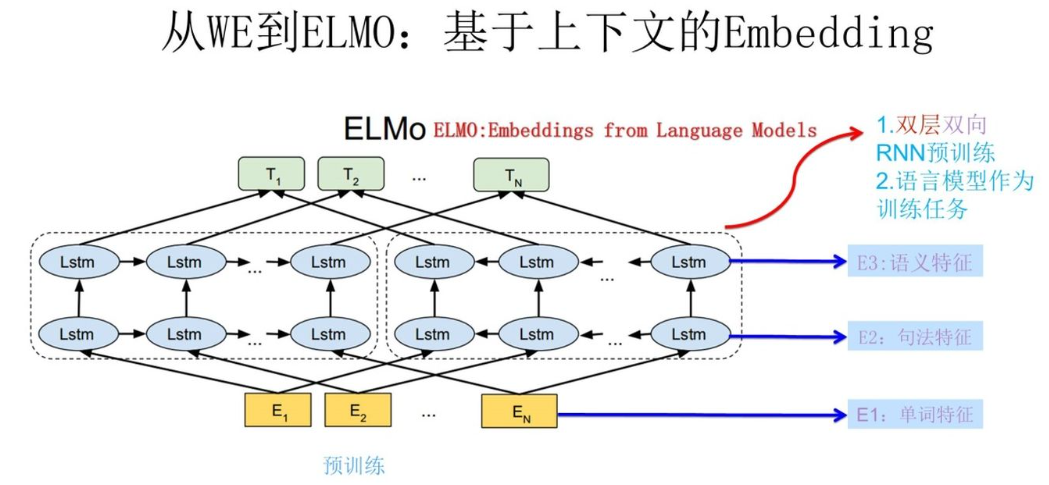
上图展示的是其第一阶段预训练过程,它的网络结构采用了双层双向 LSTM,目前语言模型训练的任务目标是根据单词 $w_i$ 的上下文去正确预测单词 $w_i$,$w_i$ 之前的单词序列 Context-before 称为上文,之后的单词序列 Context-after 称为下文。
图中左端的前向双层 LSTM 代表正方向编码器,输入的是从左到右顺序的除了预测单词外 $W_i$ 的上文 Context-before;右端的逆向双层 LSTM 代表反方向编码器,输入的是从右到左的逆序的句子下文Context-after;每个编码器的深度都是两层 LSTM 叠加。
这个网络结构其实在 NLP 中是很常用的。使用这个网络结构利用大量语料做语言模型任务就能预先训练好这个网络,如果训练好这个网络后,输入一个新句子 $s_{new}$ ,句子中每个单词都能得到对应的三个 Embedding:
- 最底层是单词的 Word Embedding;
- 往上走是第一层双向 LSTM 中对应单词位置的 Embedding,这层编码单词的句法信息更多一些;
- 再往上走是第二层 LSTM 中对应单词位置的 Embedding,这层编码单词的语义信息更多一些。
也就是说,ELMo 的预训练过程不仅仅学会单词的 Word Embedding,还学会了一个双层双向的 LSTM 网络结构,而这两者后面都有用。
Feature-based Pre-Training
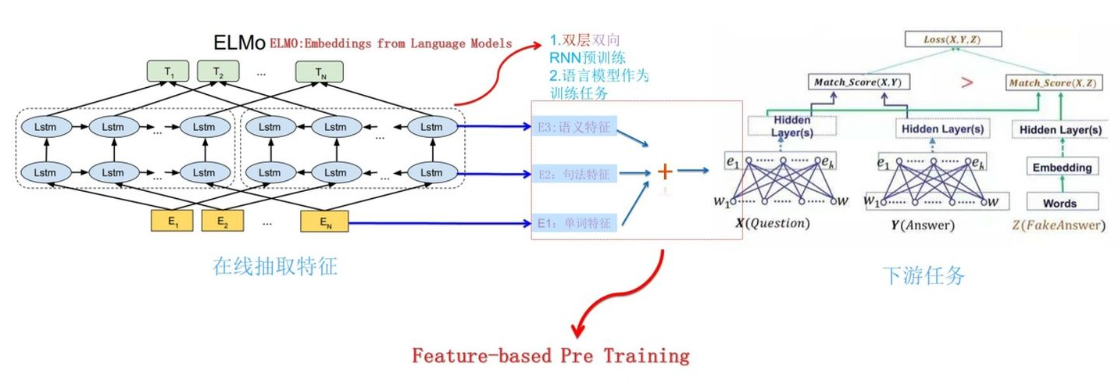
上图展示了下游任务的使用过程,比如我们的下游任务仍然是 QA 问题,此时对于问句 X:
- 我们可以先将句子 X 作为预训练好的 ELMo 网络的输入,这样句子 X 中每个单词在 ELMO 网络中都能获得对应的三个 Embedding;
- 之后给予这三个 Embedding 中的每一个 Embedding 一个权重 a,这个权重可以学习得来,根据各自权重累加求和,将三个 Embedding 整合成一个;
- 然后将整合后的这个 Embedding 作为 X 句在自己任务的那个网络结构中对应单词的输入,以此作为补充的新特征给下游任务使用。
- 对于上图所示下游任务 QA 中的回答句子 Y 来说也是如此处理。
因为 ELMo 给下游提供的是每个单词的特征形式,所以这一类预训练的方法被称为 “Feature-based Pre-Training”。
至于为何这么做能够达到区分多义词的效果,原因在于在训练好 ELMo 后,在特征提取的时候,每个单词在两层 LSTM 上都会有对应的节点,这两个节点会编码单词的一些句法特征和语义特征,并且它们的 Embedding 编码是动态改变的,会受到上下文单词的影响,周围单词的上下文不同应该会强化某种语义,弱化其它语义,进而就解决了多义词的问题。
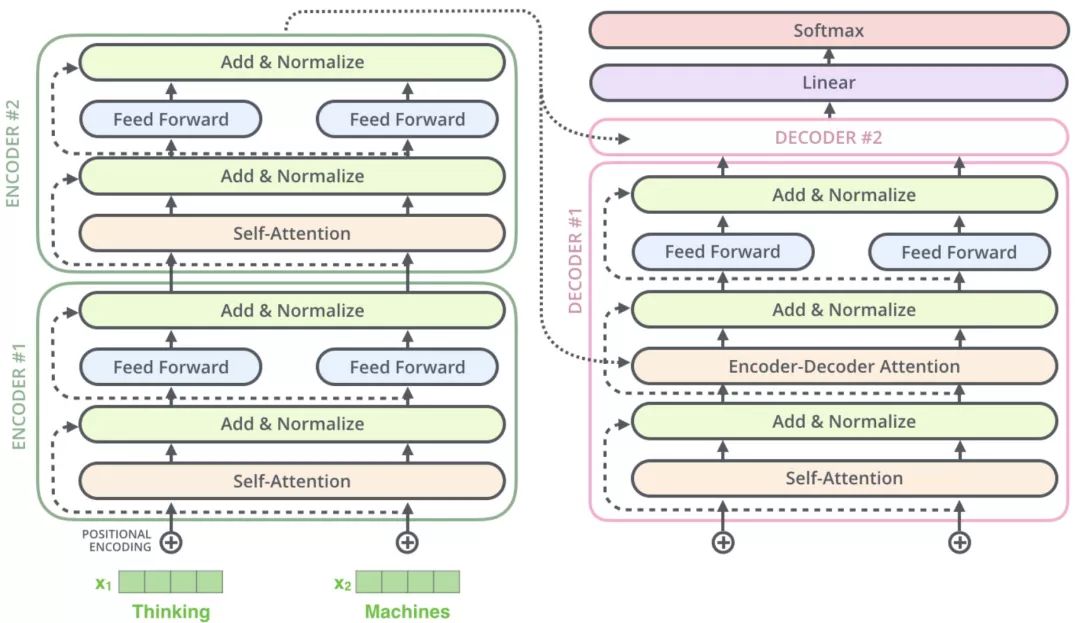
Transformer
全局
有N个encoder和N个decoder,所有encoder的结构一样但是参数不一样,decoder同理,就是所有都在一起训练。
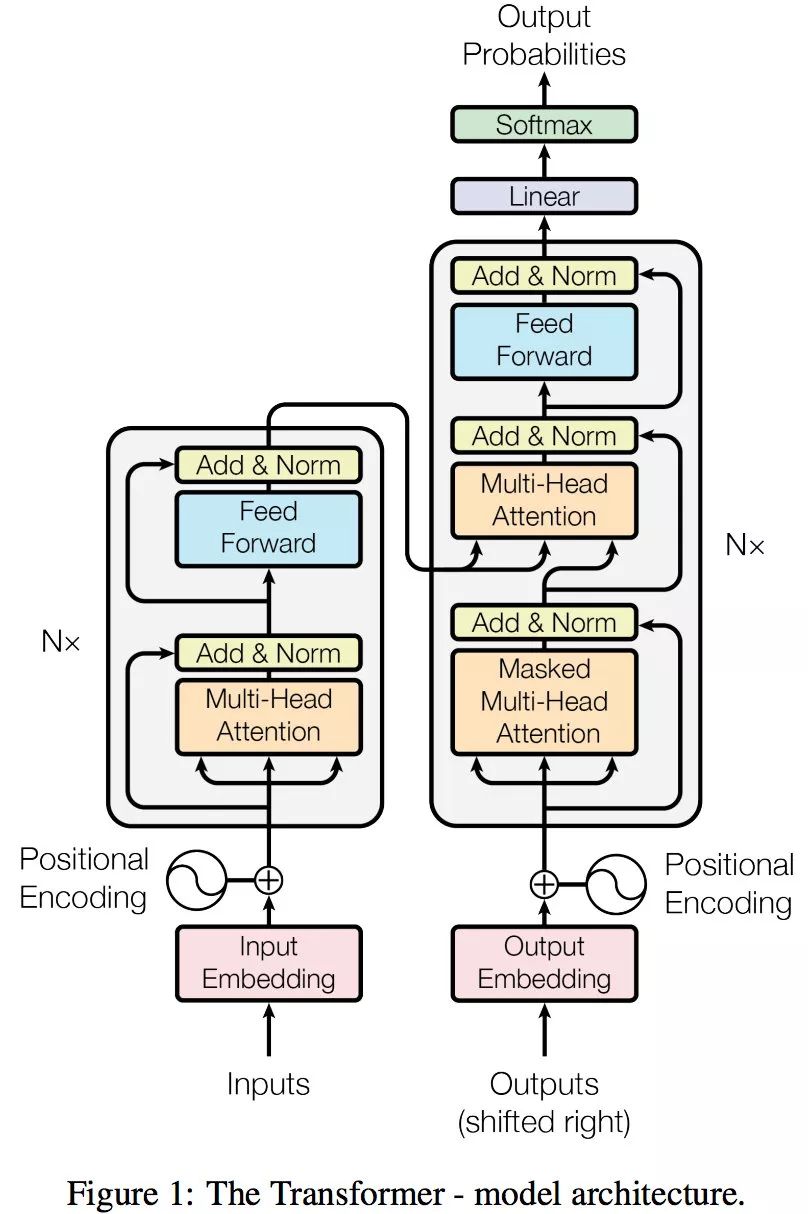
decoder比encoder多出了一个masked multi-head attention的结构,被掩盖的多头注意力机制。
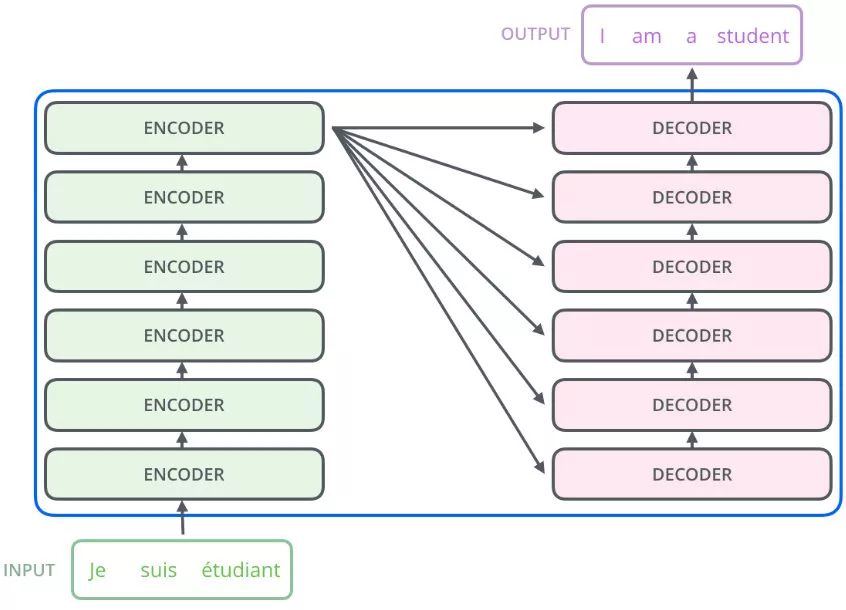
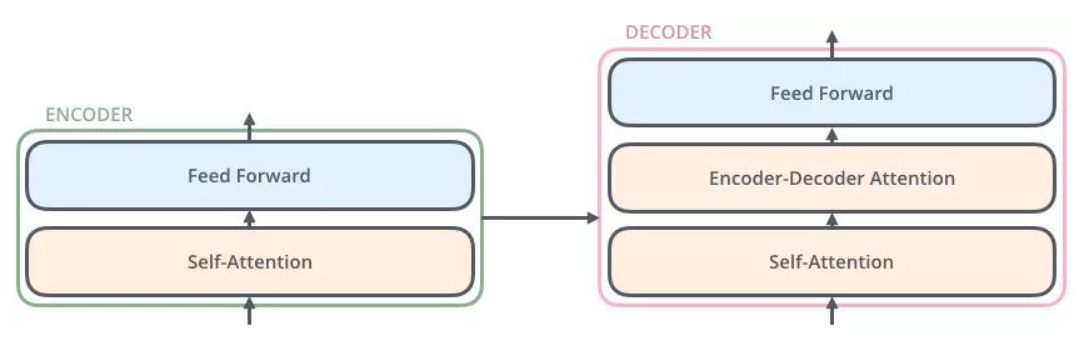
Encoder
Encoder包含两个sub-layers:
- multi-head self-attention,计算输入的self-attention
- 前馈神经网络feed- forward
每个sub-layer都模拟了残差网络,其输出是 $LayerNorm(x + SubLayer(x))$。第一层就是 $o _1 = LayerNorm(x + Attention(x))$,第二层就是 $o_2 = LayerNorm(o_1 + FeedForward(o_1))$
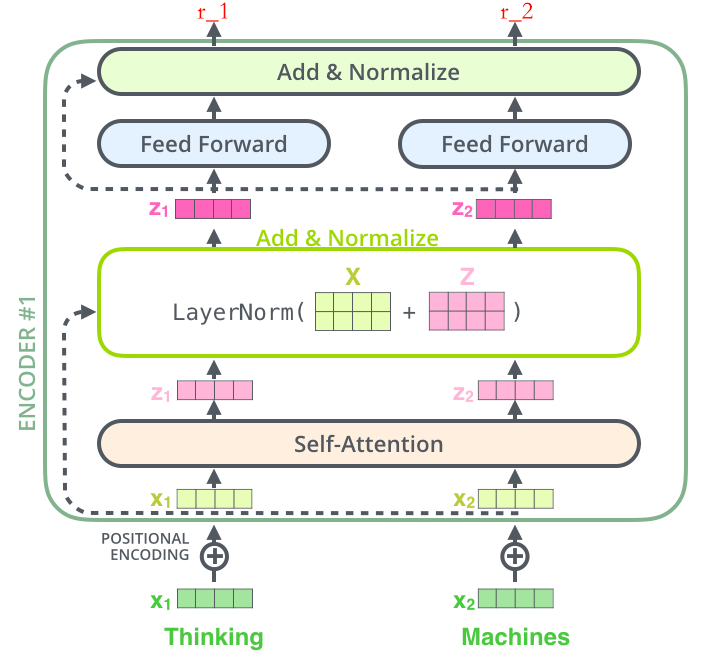
- 深绿色的 x1 表示 Embedding 层的输出,加上代表 Positional Embedding 的向量之后,得到最后输入 Encoder 中的特征向量,也就是浅绿色向量 x1;
- 浅绿色向量 x1 表示单词 “Thinking” 的特征向量,其中 x1 经过 Self-Attention 层,变成浅粉色向量 z1;
- x1 作为残差结构的直连向量,直接和 z1 相加,之后进行 Layer Norm 操作,得到粉色向量 z1;
- 残差结构的作用:避免出现梯度消失的情况
- LayerNorm 的作用:为了保证数据特征分布的稳定性,并且可以加速模型的收敛
- 为什么不用BN:BN适用于CNN和RNN等传统的神经网络结构,而LN更适用于Transformer模型这种基于自注意力机制的结构,在Transformer中,每个位置的特征都是相互独立的,因此逐位置的归一化更加合理。
- z1 经过前馈神经网络层,经过残差结构与自身相加,之后经过 LN 层,得到一个输出向量 r1;
- 该前馈神经网络包括两个线性变换和一个ReLU激活函数$FFN(x)=max(0,xW_1+b_1)W_2+b_2$
- 由于 Transformer 的 Encoders 具有 6 个 Encoder,r1也将会作为下一层 Encoder 的输入,代替 x1 的角色,如此循环,直至最后一层 Encoder。
Decoder
Decoder包含三个sub-layers:
- Masked multi-head self-attention,也是计算输入的 self-attention
- Encoder-Decoder Attention 计算,对 Encoder 的输入和 Decoder 的Masked multi-head self-attention 的输出进行 attention 计算;
- 前馈神经网络层,与 Encoder 相同。
Mask的作用
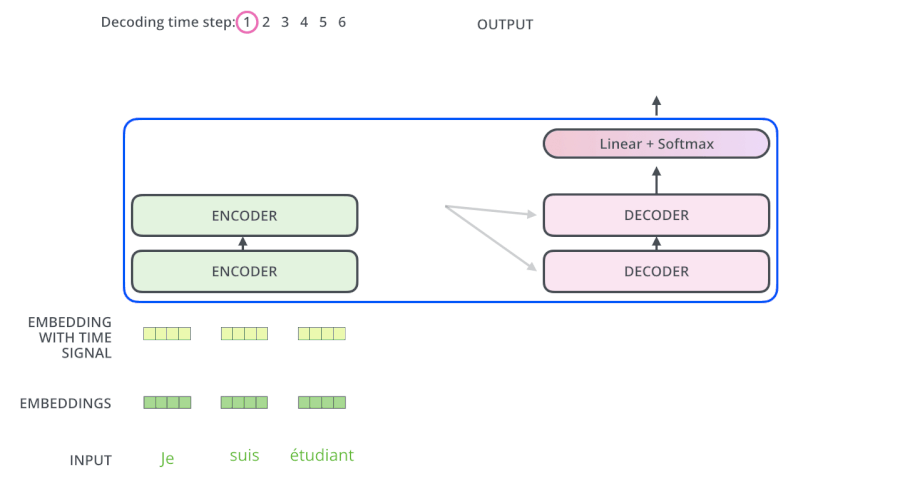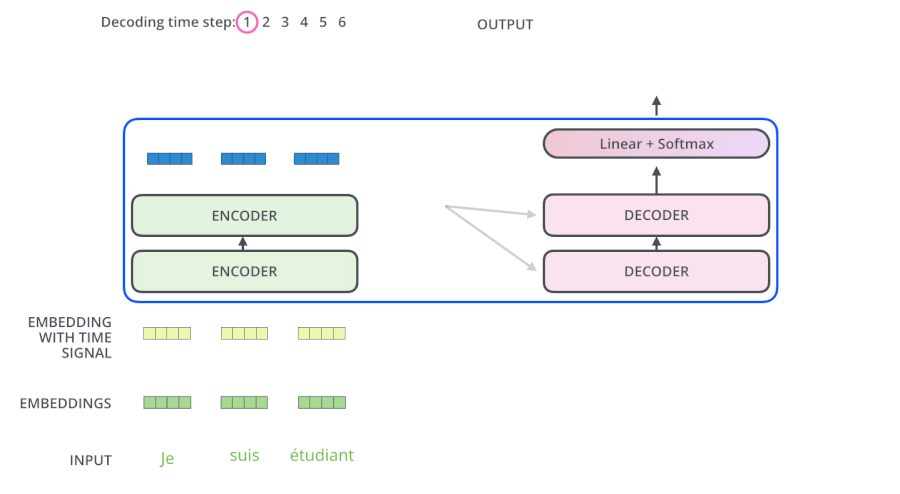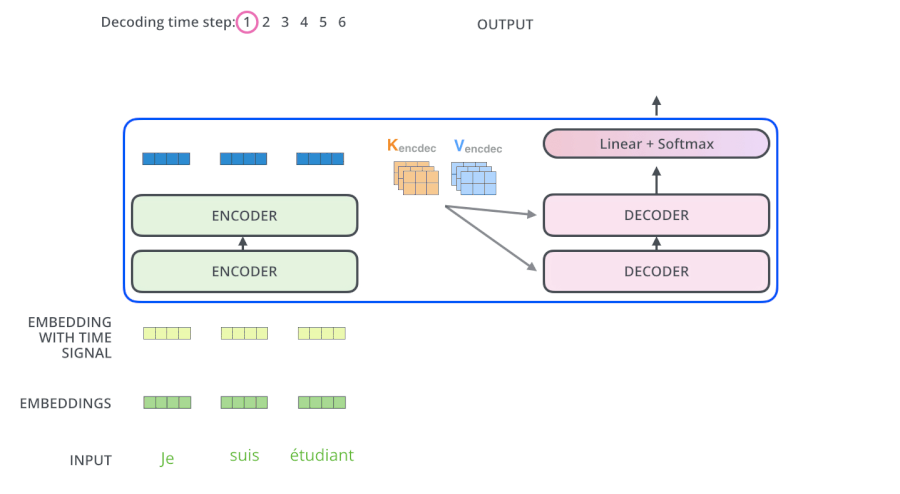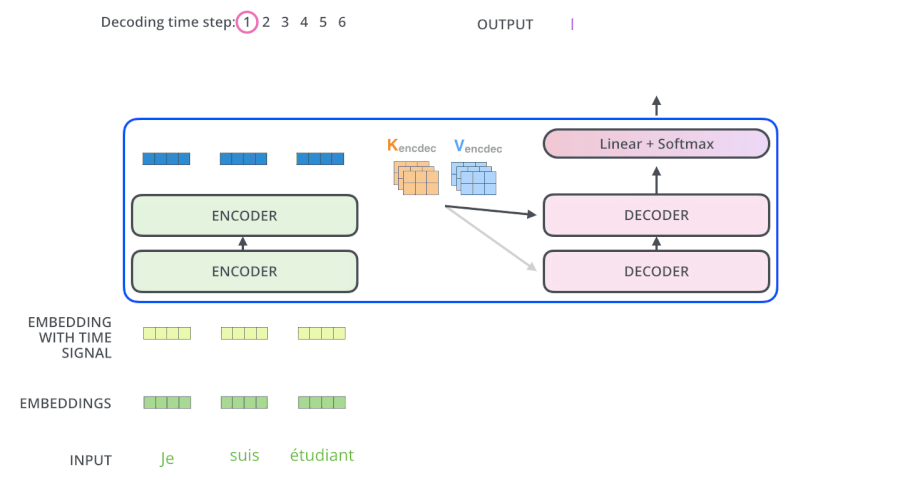
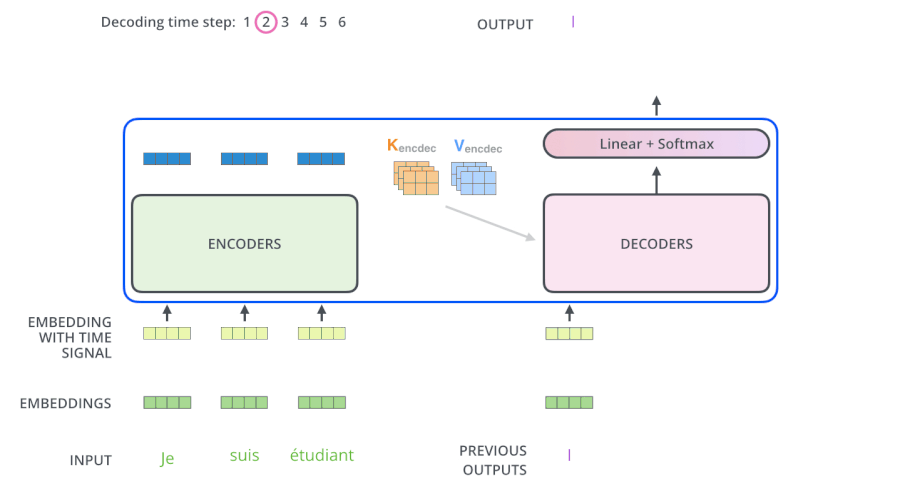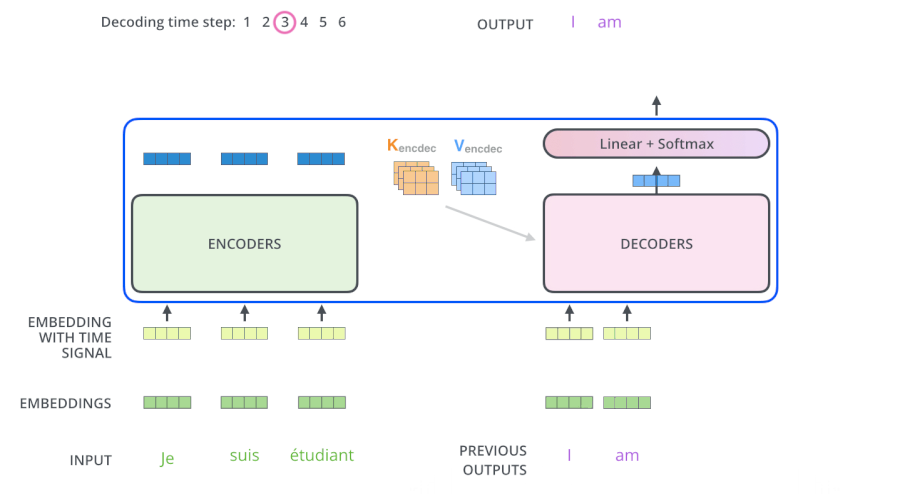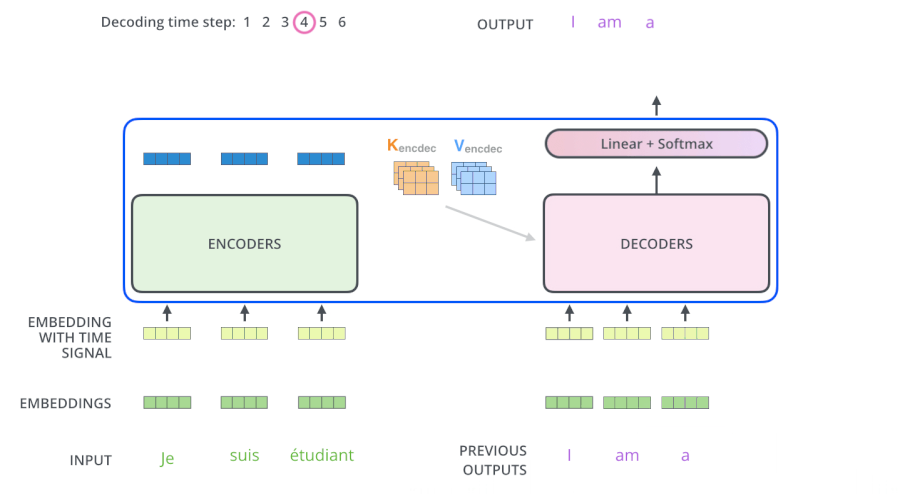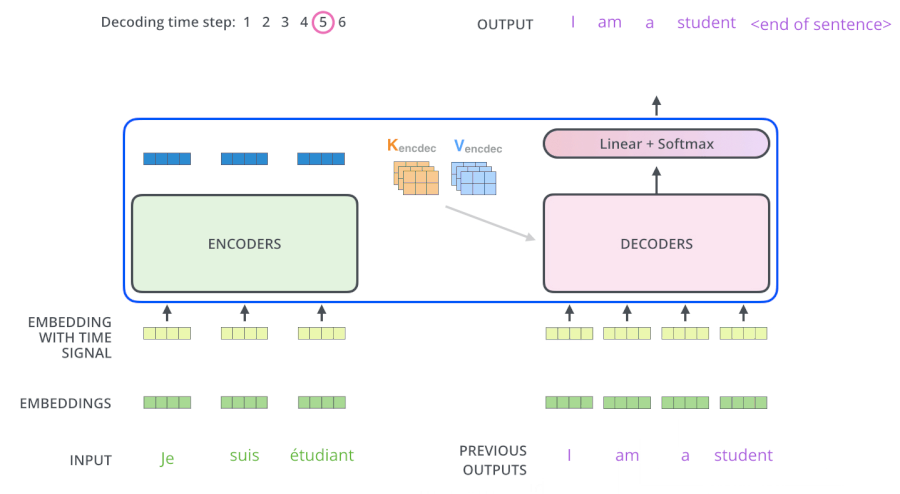
- 训练阶段:我们知道 “je suis etudiant” 的翻译结果为 “I am a student”,我们把 “I am a student” 的 Embedding 输入到 Decoders 里面,翻译第一个词 “I” 时
- 如果对 “I am a student” attention 计算不做 mask,“am,a,student” 对 “I” 的翻译将会有一定的贡献
- 如果对 “I am a student” attention 计算做 mask,“am,a,student” 对 “I” 的翻译将没有贡献
- 测试阶段:我们不知道 “我爱中国” 的翻译结果为 “I love China”,我们只能随机初始化一个 Embedding 输入到 Decoders 里面,翻译第一个词 “I” 时:
- 无论是否做 mask,“love,China” 对 “I” 的翻译都不会产生贡献
- 但是翻译了第一个词 “I” 后,随机初始化的 Embedding 有了 “I” 的 Embedding,也就是说在翻译第二词 “love” 的时候,“I” 的 Embedding 将有一定的贡献,但是 “China” 对 “love” 的翻译毫无贡献,随之翻译的进行,已经翻译的结果将会对下一个要翻译的词都会有一定的贡献,这就和做了 mask 的训练阶段做到了一种匹配
总结下就是:Decoder 做 Mask,是为了让训练阶段和测试阶段行为一致,不会出现间隙,避免过拟合。
为什么Decoder使用来自于Encoder的K、V矩阵
Query 的目的是借助它从一堆信息中找到重要的信息。
现在 Encoder 提供了 $K_e$、$V_e$ 矩阵,Decoder 提供了 $Q_d$ 矩阵,通过 “我爱中国” 翻译为 “I love China” 这句话详细解释下。
当我们翻译 “I” 的时候,由于 Decoder 提供了 $Q_d$ 矩阵,通过与 $K_e$、$V_e$ 矩阵的计算,它可以在 “我爱中国” 这四个字中找到对 “I” 翻译最有用的单词是哪几个,并以此为依据翻译出 “I” 这个单词,这就很好的体现了注意力机制想要达到的目的,把焦点放在对自己而言更为重要的信息上。
最后输出
Transformer 最后的工作是让解码器的输出通过线性层 Linear 后接上一个 softmax
- 其中线性层是一个简单的全连接神经网络,它将解码器产生的向量 A 投影到一个更高维度的向量 B 上,假设我们模型的词汇表是10000个词,那么向量 B 就有10000个维度,每个维度对应一个惟一的词的得分。
- 之后的softmax层将这些分数转换为概率。选择概率最大的维度,并对应地生成与之关联的单词作为此时间步的输出就是最终的输出
动态过程
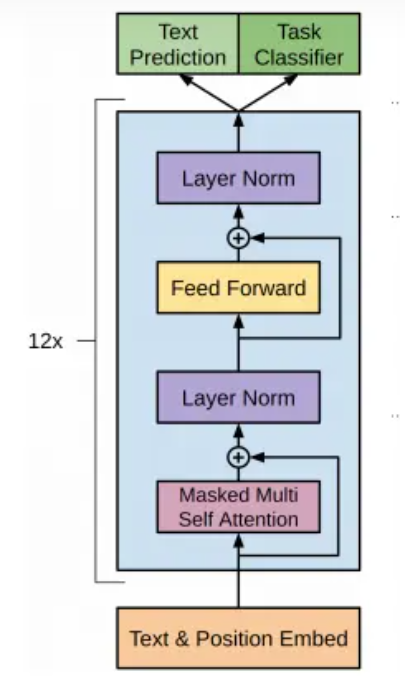
GPT
Generative Pre-Training Transformer
使用了单向的Transformer。在Transformer的文章中,提到了Encoder与Decoder使用的Transformer Block是不同的。在Decoder Block中,使用了Masked Self-Attention,即句子中的每个词,都只能对包括自己在内的前面所有词进行Attention,这就是单向Transformer。GPT使用的Transformer结构就是将Encoder中的Self-Attention替换成了Masked Self-Attention
预训练
除了以 ELMo 为代表的这种基于特征融合的预训练方法外,NLP 里还有一种典型做法,这种做法和图像领域的方式就是看上去一致的了,一般将这种方法称为 “基于Fine-tuning的模式”,而 GPT 就是这一模式的典型开创者。
GPT也采用两阶段过程:
- 第一个阶段:利用语言模型进行预训练;
- 第二个阶段:通过 Fine-tuning 的模式解决下游任务。
上图展示了 GPT 的预训练过程,其实和 ELMo 是类似的,主要不同在于两点:
- 首先,特征抽取器用的不是 RNN,而是用的 Transformer,它的特征抽取能力要强于RNN,这个选择很明显是很明智的;
- 其次,
- GPT 的预训练虽然仍然是以语言模型作为目标任务,但是采用的是单向的语言模型,所谓 “单向” 的含义是指:语言模型训练的任务目标是根据 $w_i$单词的上下文去正确预测单词 $w_i$ 。
- ELMo 在做语言模型预训练的时候,预测单词 $w_i$ 同时使用了上文和下文,而 GPT 则只采用 Context-before 这个单词的上文来进行预测,而抛开了下文。
- GPT 这个选择现在看不是个太好的选择,原因很简单,它没有把单词的下文融合进来,这限制了其在更多应用场景的效果,比如阅读理解这种任务,在做任务的时候是可以允许同时看到上文和下文一起做决策的。如果预训练时候不把单词的下文嵌入到 Word Embedding 中,是很吃亏的,白白丢掉了很多信息。
Fine-tuning
- 首先,对于不同的下游任务来说,本来可以任意设计自己的网络结构,现在不行了,你要向 GPT 的网络结构看齐,把任务的网络结构改造成和 GPT 一样的网络结构。
- 然后,在做下游任务的时候,利用第一步预训练好的参数初始化 GPT 的网络结构,这样通过预训练学到的语言学知识就被引入到你手头的任务里来了。
- 再次,你可以用手头的任务去训练这个网络,对网络参数进行 Fine-tuning,使得这个网络更适合解决手头的问题。
BERT
Bidirectional Encoder Representations from Transformers
一个真正的集大成者:参考了 ELMO 模型的双向编码思想、借鉴了 GPT 用 Transformer 作为特征提取器的思路、采用了 word2vec 所使用的 CBOW $^{[1]}$方法
$[1]$ Word2Vec 有两种训练方法:
- 第一种叫 CBOW,核心思想是从一个句子里面把一个词抠掉,用这个词的上文和下文去预测被抠掉的这个词;
- 第二种叫做 Skip-gram,和 CBOW 正好反过来,输入某个单词,要求网络预测它的上下文单词。
- BERT 和 GPT 之间的区别:
- GPT:GPT 使用 Transformer Decoder 作为特征提取器、具有良好的文本生成能力,然而当前词的语义只能由其前序词决定,并且在语义理解上不足
- BERT:使用了 Transformer Encoder 作为特征提取器,并使用了与其配套的掩码训练方法。虽然使用双向编码让 BERT 不再具有文本生成能力,但是 BERT 的语义信息提取能力更强
- 单向编码和双向编码的差异,以该句话举例 “今天天气很{},我们不得不取消户外运动”,分别从单向编码和双向编码的角度去考虑 {} 中应该填什么词:
- 单向编码:单向编码只会考虑 “今天天气很”,以人类的经验,大概率会从 “好”、“不错”、“差”、“糟糕” 这几个词中选择,这些词可以被划为截然不同的两类
- 双向编码:双向编码会同时考虑上下文的信息,即除了会考虑 “今天天气很” 这五个字,还会考虑 “我们不得不取消户外运动” 来帮助模型判断,则大概率会从 “差”、“糟糕” 这一类词中选择
结构
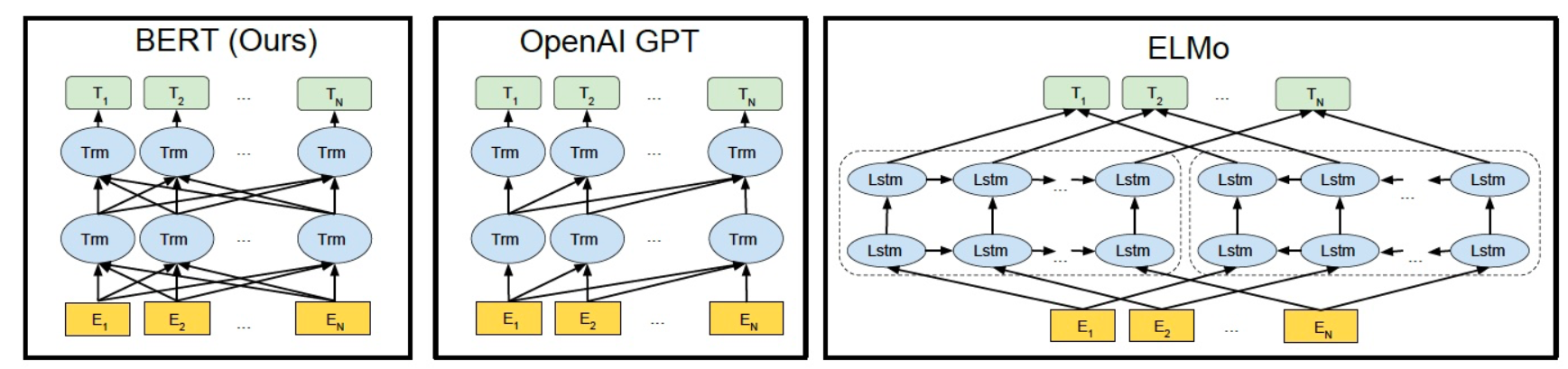
ELMo 使用自左向右编码和自右向左编码的两个 LSTM 网络,分别以$ P(w_i|w_1,⋯,w_{i−1})$ 和 $P(w_i|w_{i+1},⋯,w_n)$为目标函数独立训练,将训练得到的特征向量以拼接的形式实现双向编码,本质上还是单向编码,只不过是两个方向上的单向编码的拼接而成的双向编码。
GPT 使用 Transformer Decoder 作为 Transformer Block,以 $ P(w_i|w_1,⋯,w_{i−1})$ 为目标函数进行训练,用 Transformer Block 取代 LSTM 作为特征提取器,实现了单向编码,是一个标准的预训练语言模型,即使用 Fine-Tuning 模式解决下游任务。
BERT 也是一个标准的预训练语言模型,
它以 $P(w_i|w_1,⋯,w_{i−1},w_{i+1},⋯,w_n)$为目标函数进行训练,BERT 使用的编码器属于双向编码器。
- BERT 和 ELMo 的区别在于使用 Transformer Block 作为特征提取器,加强了语义特征提取的能力;
- BERT 和 GPT 的区别在于使用 Transformer Encoder 作为Transformer Block,并且将 GPT 的单向编码改成双向编码,也就是说 BERT 舍弃了文本生成能力,换来了更强的语义理解能力。
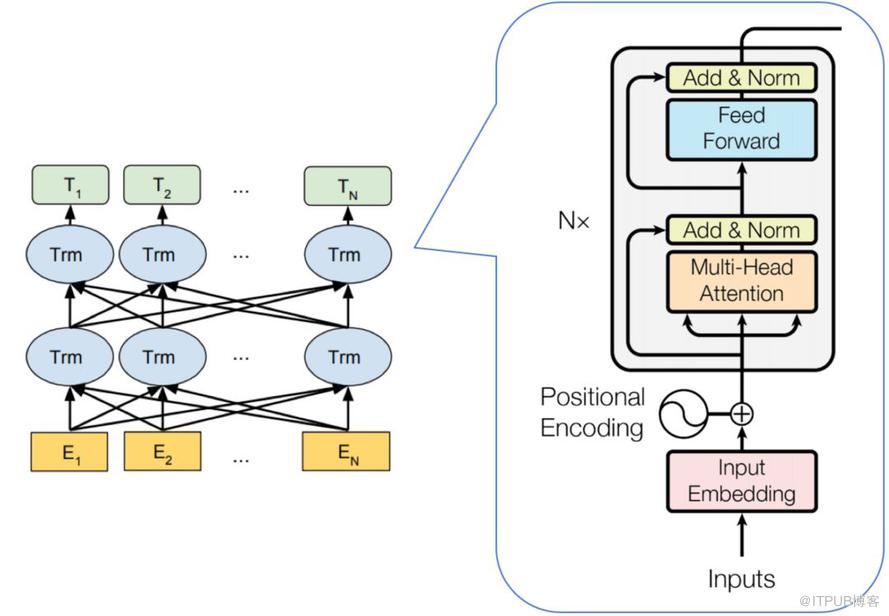
无监督训练
和 GPT 一样,BERT 也采用二段式训练方法:
- 第一阶段:使用易获取的大规模无标签余料,来训练基础语言模型;
- 第二阶段:根据指定任务的少量带标签训练数据进行微调训练。
不同于 GPT 等标准语言模型使用 $ P(w_i|w_1,⋯,w_{i−1})$ 为目标函数进行训练,能看到全局信息的 BERT 使用 $P(w_i|w_1,⋯,w_{i−1},w_{i+1},⋯,w_n)$ 为目标函数进行训练。
BERT 用语言掩码模型(MLM)方法训练词的语义理解能力;用下句预测(NSP)方法训练句子之间的理解能力,从而更好地支持下游任务。
MLM
MLM 方法也就是随机去掉句子中的部分 token(单词),然后模型来预测被去掉的 token 是什么。这样实际上已经不是传统的神经网络语言模型(类似于生成模型)了,而是单纯作为分类问题,根据这个时刻的 hidden state 来预测这个时刻的 token 应该是什么,而不是预测下一个时刻的词的概率分布了。
随机去掉的 token 被称作掩码词,在训练中,掩码词将以 15% 的概率被替换成 [MASK],也就是说随机 mask 语料中 15% 的 token,这个操作则称为掩码操作。注意:在CBOW 模型中,每个词都会被预测一遍。
但是这样设计 MLM 的训练方法会引入弊端:在模型微调训练阶段或模型推理(测试)阶段,输入的文本中将没有 [MASK],进而导致产生由训练和预测数据偏差导致的性能损失。
考虑到上述的弊端,BERT 并没有总用 [MASK] 替换掩码词,而是按照一定比例选取替换词。在选择 15% 的词作为掩码词后这些掩码词有三类替换选项:
- 80% 练样本中:将选中的词用 [MASK] 来代替
1 | “地球是[MASK]八大行星之一” |
- 10% 的训练样本中:选中的词不发生变化,该做法是为了缓解训练文本和预测文本的偏差带来的性能损失
1 | “地球是太阳系八大行星之一” |
- 10% 的训练样本中:将选中的词用任意的词来进行代替,该做法是为了让 BERT 学会根据上下文信息自动纠错
1 | “地球是苹果八大行星之一” |
NSP
单词预测粒度的训练到不了句子关系这个层级,为了学会捕捉句子之间的语义联系,BERT 采用了下句预测(NSP )作为无监督预训练的一部分。
NSP 的具体做法是,BERT 输入的语句将由两个句子构成,其中,50% 的概率将语义连贯的两个连续句子作为训练文本(连续句对一般选自篇章级别的语料,以此确保前后语句的语义强相关),另外 50% 的概率将完全随机抽取两个句子作为训练文本。
1 | 连续句对:[CLS]今天天气很糟糕[SEP]下午的体育课取消了[SEP] |
其中 [SEP] 标签表示分隔符。 [CLS] 表示标签用于类别预测,结果为 1,表示输入为连续句对;结果为 0,表示输入为随机句对。
通过训练 [CLS] 编码后的输出标签,BERT 可以学会捕捉两个输入句对的文本语义,在连续句对的预测任务中,BERT 的正确率可以达到 97%-98%。
BERT的输入
BERT 在预训练阶段使用了前文所述的两种训练方法,在真实训练中一般是两种方法混合使用。
由于 BERT 通过 Transformer 模型堆叠而成,所以 BERT 的输入需要两套 Embedding 操作:
- 一套为 One-hot 词表映射编码(对应下图的 Token Embeddings);
- 另一套为位置编码(对应下图的 Position Embeddings),不同于 Transformer 的位置编码用三角函数表示,BERT 的位置编码将在预训练过程中训练得到(训练思想类似于Word Embedding 的 Q 矩阵)
- 由于在 MLM 的训练过程中,存在单句输入和双句输入的情况,因此 BERT 还需要一套区分输入语句的分割编码(对应下图的 Segment Embeddings),BERT 的分割编码也将在预训练过程中训练得到
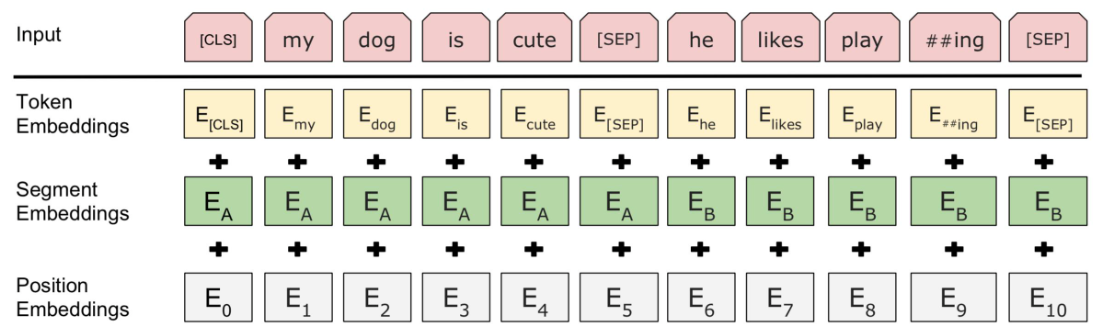
对于分割编码,Segment Embeddings 层只有两种向量表示。前一个向量是把 0 赋给第一个句子中的各个 token,后一个向量是把 1 赋给第二个句子中的各个 token ;如果输入仅仅只有一个句子,那么它的 segment embedding 就是全 0,下面我们简单举个例子描述下:
[CLS]I like dogs[SEP]I like cats[SEP] 对应编码 0 0 0 0 0 1 1 1 1
[SEP]I Iike dogs and cats[SEP] 对应编码 0 0 0 0 0 0 0
下游任务改造
句对分类
给定两个句子,判断它们的关系,称为句对分类,例如判断句对是否相似、判断后者是否为前者的答案。
针对句对分类任务,BERT 在预训练过程中就使用了 NSP 训练方法获得了直接捕获句对语义关系的能力。
如下图所示,句对用 [SEP] 分隔符拼接成文本序列,在句首加入标签 [CLS],将句首标签所对应的输出值作为分类标签,计算预测分类标签与真实分类标签的交叉熵,将其作为优化目标,在任务数据上进行微调训练。
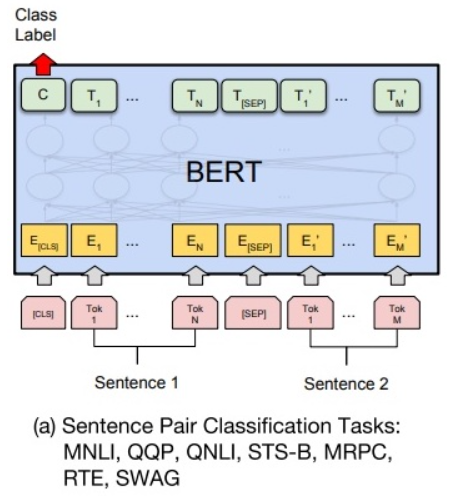
针对二分类任务,BERT 不需要对输入数据和输出数据的结构做任何改动,直接使用与 NSP 训练方法一样的输入和输出结构就行。
针对多分类任务,需要在句首标签 [CLS] 的输出特征向量后接一个全连接层和 Softmax 层,保证输出维数与类别数目一致,最后通过 arg max 操作(取最大值时对应的索引序号)得到相对应的类别结果。
下面给出句对分相似性任务的实例:
任务:判断句子 “我很喜欢你” 和句子 “我很中意你” 是否相似
输入改写:“[CLS]我很喜欢你[SEP]我很中意你”
取 “[CLS]” 标签对应输出:[0.02, 0.98]
通过 arg max 操作得到相似类别为 1(类别索引从 0 开始),即两个句子相似
单句分类
给定一个句子,判断该句子的类别,统称为单句分类,例如判断情感类别、判断是否为语义连贯的句子。
针对单句二分类任务,也无须对 BERT 的输入数据和输出数据的结构做任何改动。
如下图所示,单句分类在句首加入标签 [CLS],将句首标签所对应的输出值作为分类标签,计算预测分类标签与真实分类标签的交叉熵,将其作为优化目标,在任务数据上进行微调训练。
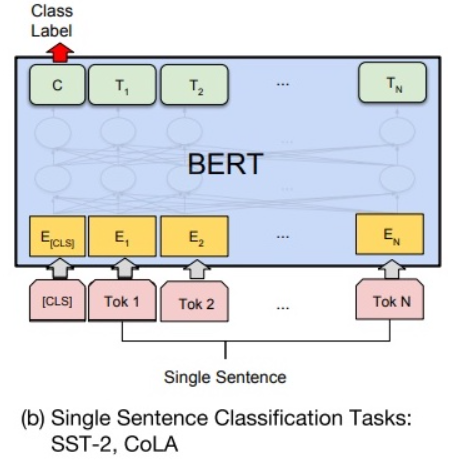
同样,针对多分类任务,需要在句首标签 [CLS] 的输出特征向量后接一个全连接层和 Softmax 层,保证输出维数与类别数目一致,最后通过 argmax 操作得到相对应的类别结果。
下面给出语义连贯性判断任务的实例:
任务:判断句子“海大球星饭茶吃” 是否为一句话
输入改写:“[CLS]海大球星饭茶吃”
取 “[CLS]” 标签对应输出:[0.99, 0.01]
通过 arg max 操作得到相似类别为 0,即这个句子不是一个语义连贯的句子
文本回答
给定一个问句和一个蕴含答案的句子,找出答案在后这种的位置,称为文本问答,例如给定一个问题(句子 A),在给定的段落(句子 B)中标注答案的其实位置和终止位置。
文本问答任何和前面讲的其他任务有较大的差别,无论是在优化目标上,还是在输入数据和输出数据的形式上,都需要做一些特殊的处理。
为了标注答案的起始位置和终止位置,BERT 引入两个辅助向量 s(start,判断答案的起始位置) 和 e(end,判断答案的终止位置)。
如下图所示,BERT 判断句子 B 中答案位置的做法是,将句子 B 中的每一个次得到的最终特征向量 $T′_i$ 经过全连接层(利用全连接层将词的抽象语义特征转化为任务指向的特征)后,分别与向量 s 和 e 求内积,对所有内积分别进行 softmax 操作,即可得到词 Tok m(m∈[1,M])作为答案其实位置和终止位置的概率。最后,去概率最大的片段作为最终的答案。
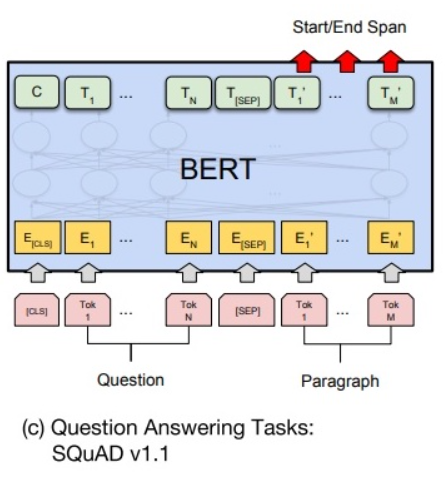
文本回答任务的微调训练使用了两个技巧:
- 用全连接层把 BERT 提取后的深层特征向量转化为用于判断答案位置的特征向量
- 引入辅助向量 s 和 e 作为答案其实位置和终止位置的基准向量,明确优化目标的方向和度量方法
下面给出文本问答任务的实例:
任务:给定问句 “今天的最高温度是多少”,在文本 “天气预报显示今天最高温度 37 摄氏度” 中标注答案的起始位置和终止位置
输入改写:“[CLS]今天的最高温度是多少[SEP]天气预报显示今天最高温度 37 摄氏度”
BERT Softmax 结果:
篇章文本 天气 预报 显示 今天 最高温 37 摄氏度 起始位置概率 0.01 0.01 0.01 0.04 0.10 0.80 0.03 终止位置概率 0.01 0.01 0.01 0.03 0.04 0.10 0.80 对 Softmax 的结果取 arg max,得到答案的起始位置为 6,终止位置为 7,即答案为 “37 摄氏度”
单句标注
给定一个句子,标注每个次的标签,称为单句标注。例如给定一个句子,标注句子中的人名、地名和机构名。
单句标注任务和 BERT 预训练任务具有较大差异,但与文本问答任务较为相似。
如下图所示,在进行单句标注任务时,需要在每个词的最终语义特征向量之后添加全连接层,将语义特征转化为序列标注任务所需的特征,单句标注任务需要对每个词都做标注,因此不需要引入辅助向量,直接对经过全连接层后的结果做 Softmax 操作,即可得到各类标签的概率分布。
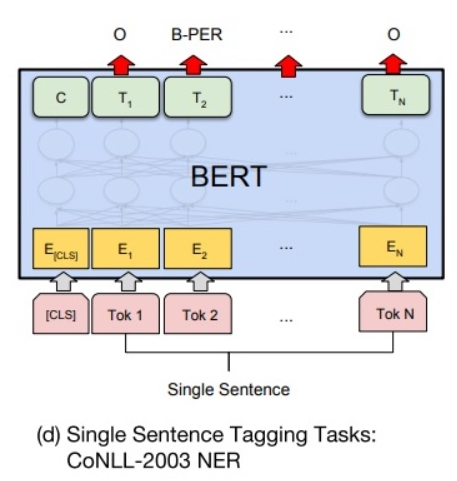
由于 BERT 需要对输入文本进行分词操作,独立词将会被分成若干子词,因此 BERT 预测的结果将会是 5 类(细分为 13 小类):
- O(非人名地名机构名,O 表示 Other)
- B-PER/LOC/ORG(人名/地名/机构名初始单词,B 表示 Begin)
- I-PER/LOC/ORG(人名/地名/机构名中间单词,I 表示 Intermediate)
- E-PER/LOC/ORG(人名/地名/机构名终止单词,E 表示 End)
- S-PER/LOC/ORG(人名/地名/机构名独立单词,S 表示 Single)
将 5 大类的首字母结合,可得 IOBES,这是序列标注最常用的标注方法。
下面给出命名实体识别(NER)任务的示例:
任务:给定句子 “爱因斯坦在柏林发表演讲”,根据 IOBES 标注 NER 结果
输入改写:“[CLS]爱 因 斯坦 在 柏林 发表 演讲”
BERT Softmax 结果:
BOBES 爱 因 斯坦 在 柏林 发表 演讲 O 0.01 0.01 0.01 0.90 0.01 0.90 0.90 B-PER 0.90 0.01 0.01 0.01 0.01 0.01 0.01 I-PER 0.01 0.90 0.01 0.01 0.01 0.01 0.01 E-PER 0.01 0.01 0.90 0.01 0.01 0.01 0.01 S-LOC 0.01 0.01 0.01 0.01 0.01 0.01 0.01 对 Softmax 的结果取 arg max,得到最终地 NER 标注结果为:“爱因斯坦” 是人名;“柏林” 是地名