周志华西瓜书学习笔记
二周目补充版
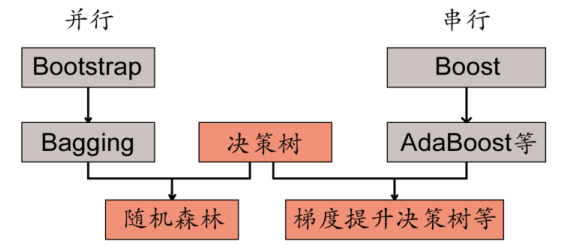
Bagging:训练多个分类器(并行,分类器之间关系弱)取平均
- $f(x) = \frac{1}{M} \sum \limits _{m=1} ^{M} f _m(x)$
Boosting:提升算法,从弱学习器开始加强,通过加权来进行训练(串行)。
- $F _m(x) = F _{m-1}(x) + argmin _h \sum \limits _{i=1} ^{n} L(y_i, F _{m-1}(x_i) + h(x_i))$
Stacking:聚合多个分类或回归模型(可以分阶段做)
Bagging
全称:bootstrap aggregation
介绍
最典型的就是随机/森林 Random Forest,并行和独立地去建立树
- 随机:数据采样随机,特征选择随机;
- 数据要好而不同,需要多样性,增加泛化能力 => 改变输入数据
- 数据随机采样:比如有100条数据,每棵树都随机取80个(80%)
- 特征选择随机:多个特征,每次也随机采样部分(60%)
- 森林:很多个决策树并行放在一起
- 分类任务:少数服从多数,第一棵树=>A,第二棵树=>B,第三棵树=>A,随后投票取A;
- 回归任务:值取平均。
优势
- 能够处理很高维度(Feature多)的数据,并且不用做特征选择
- 训练完后能够给出哪些feature比较重要(集成学习的优点)
- B特征存在的时候算出目前的错误率,然后破坏掉B特征加入噪声什么的,保证ACD特征一样的情况下算出B‘特征下的特征率,如果err1和err2近似,说明B不重要,反之
- 容易做成并行化方法,处理速度快
- 可以进行可视化展示,便于分析
Boosting
介绍
$$F _m(x) = F _{m-1}(x) + argmin _h \sum \limits _{i=1} ^{n} L(y_i, F _{m-1}(x_i) + h(x_i))$$
$F _{m-1}(x)$是前一轮,后面是当前这一轮,加一棵新的树的时候是有要求的:每加入一棵树,这棵要比前面的强,因此去计算他的loss看loss有没有下降
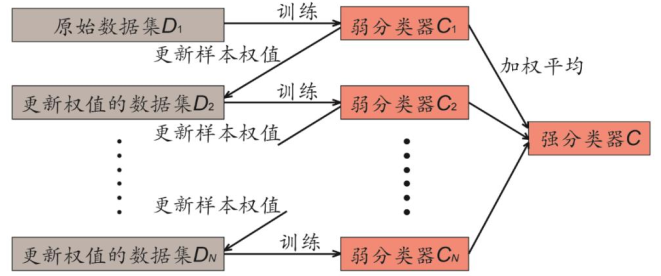
AdaBoost
基本介绍
AdaBoost会根据前一次的分类效果调整数据权重,如果一个数据在某次分错了,那么就在下一次给他更大的权重。
每次自适应地改变样本权重并训练弱分类器,最终,每个弱分类器都可以计算出它的加权训练样本分类错误率,将全部弱分类器按一定权值进行组合得到强分类器,错误率越低的弱分类器所占权重越高。
主要参数
| 参数类别 | 参数 | 说明 |
|---|---|---|
| 框架参数 | n_estimators | 最大的弱学习器的个数。一般来说 n_estimators 太小,容易欠拟合, n_estimators 太大,又容易过拟合,在实际调参的过程中,常常将 n_estimators 和 learning_rate 一起考虑。 |
| 框架参数 | learning_rate | 每个弱学习器的权重缩减系数 ν,也称作步长, ν 的取值范围为 0<ν≤1。 对于同样的训练集拟合效果,较小的 ν 意味着需要更多的弱学习器的 迭代次数。 |
| 弱学习器参数 | max_features | 决策树划分时考虑的最大特征数,默认考虑全部特征,如果特征数非 常多,可以取部分特征,以控制决策树的生成时间。 |
| 弱学习器参数 | max_depth | 决策树最大深度,如果模型样本量多,特征也多的情况下,推荐限制 这个最大深度。 |
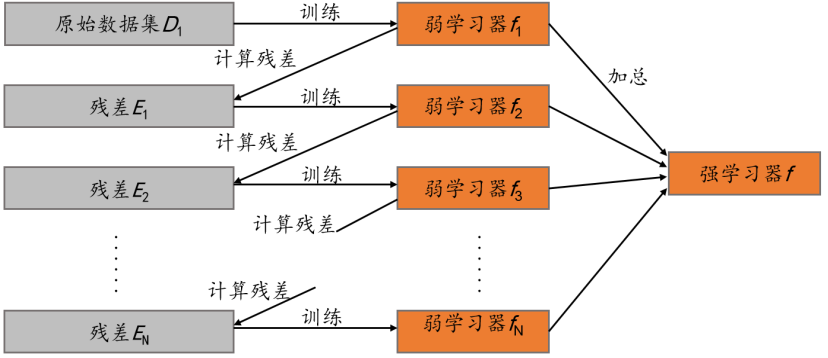
GBDT
基本介绍
梯度提升决策树 GBDT 是一种 Boosting 集成学习算法,但是却和传统的 AdaBoost 有很大的不同,且弱学习器限定了只能使用 CART 回归树模型。在 GBDT 的迭代中,假设前一轮迭代得到的强学习器是$𝑓_{t-1}(x)$, 损失函数是 $L(y, 𝑓_{t-1}(x))$, 本轮迭代的目标是得到一个 CART 回归树(基于基尼系数)模型的弱学习器ℎ𝑡(𝑥),使得本轮的损失 $L(y_i, F _{m-1}(x_i) + h(x_i))$ 最小。也就是说,本轮迭代得到的决策树,要让样本的损失尽量变得更小。
1 | A -> B -> C |
主要参数
| 参数类别 | 参数 | 说明 |
|---|---|---|
| 框架参数 | n_estimators | 最大的弱学习器的个数。一般来说 n_estimators 太小,容易欠拟合, n_estimators 太大,又容易过拟合,在实际调参的过程中,常常将 n_estimators 和 learning_rate 一起考虑。 |
| 框架参数 | learning_rate | 每个弱学习器的权重缩减系数 ν,也称作步长, ν 的取值范围为 0<ν≤1。 对于同样的训练集拟合效果,较小的 ν 意味着需要更多的弱学习器的 迭代次数。 |
| 框架参数 | subsample | 子采样率,取值为(0,1],如果取值为 1,则全部样本都使用,等于没 有使用子采样。如果取值小于 1,则只有一部分样本会去做 GBDT 的 决策树拟合。选择小于 1 的比例可以减少方差,即防止过拟合,但是 会增加样本拟合的偏差,因此取值不能太低。 |
| 弱学习器参数 | max_features | 决策树划分时考虑的最大特征数,默认考虑全部特征,如果特征数非 常多,可以取部分特征,以控制决策树的生成时间。 |
| 弱学习器参数 | max_depth | 决策树最大深度,如果模型样本量多,特征也多的情况下,推荐限制 这个最大深度。 |
XgBoost
基本介绍
GBDT的一种高效实现。相比于传统的 GBDT 算法, XGBoost 在损失函数、正则化、切分点查找和并行化设计等方面进行了改进,使得其在计算速度上比常见工具包快 5 倍以上。例如,GBDT 算法在训练第 n 棵树时需要用到第 n-1 棵树的残差,从而导致算法较难实现并行;而 XGBoost 通过对目标函数做二阶泰勒展开,使得最终的目标函数只依赖每个数据点上损失函数的一阶导和二阶导,进而容易实现并行。
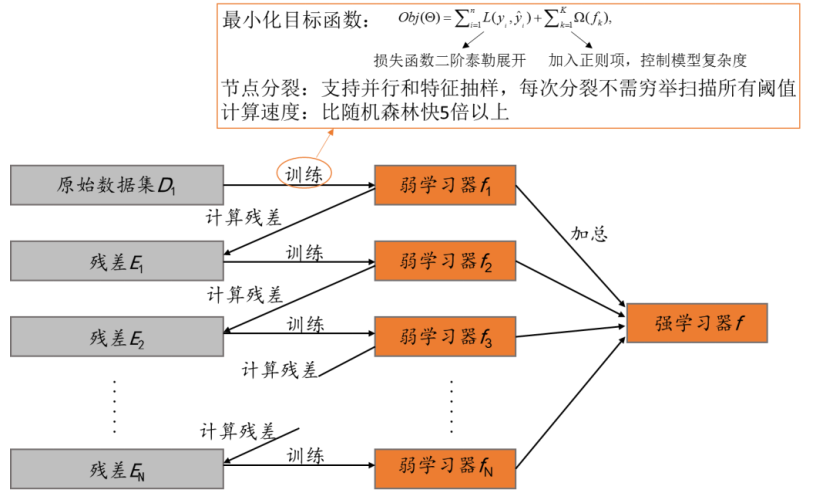
相比GBDT的优势
(1) 传统 GBDT 在优化时只用到了损失函数的一阶导数信息, XGBoost 则对损失函数进行了二阶泰勒展开,用到了一阶和二阶导数信息。并且 XGBoost 可以自定义损失函数,只要损失函数一阶和二阶可导。
(2) XGBoost 在损失函数里加入了正则项,用于控制模型的复杂度。从方差和偏差权衡的角度来讲,正则项降低了模型的方差,使训练得出的模型更加简单,能防止过拟合,这也是XGBoost 优于传统 GBDT 的一个特性。
(3) 传统 GBDT以 CART树作为弱分类器, XGBoost还支持线性分类器作为弱分类器,此时 XGBoost 相当于包含了 L1 和 L2 正则项的 Logistic 回归(分类问题)或者线性回归(回归问题)。
(4) XGBoost 借鉴了随机森林的做法,支持特征抽样,在训练弱学习器时,只使用抽样出来的部分特征。这样不仅能降低过拟合,还能减少计算。
(5) XGBoost 支持并行。但是 XGBoost 的并行不是指能够并行地训练决策树,XGBoost 也是训练完一棵决策树再训练下一棵决策树的。 XGBoost 是在处理特征的层面上实现并行的。我们知道,训练决策树最耗时的一步就是对各个特征的值进行排序(为了确定最佳分割点)并计算信息增益, XGBoost 对于各个特征的信息增益计算就可以在多线程中进行
主要参数
| 参数类别 | 参数 | 说明 |
|---|---|---|
| 框架参数 | n_estimators | 最大的弱学习器的个数。一般来说 n_estimators 太小,容易欠拟合, n_estimators 太大,又容易过拟合,在实际调参的过程中,常常将 n_estimators 和 learning_rate 一起考虑。 |
| 框架参数 | learning_rate | 每个弱学习器的权重缩减系数 ν,也称作步长, ν 的取值范围为 0<ν≤1。 对于同样的训练集拟合效果,较小的 ν 意味着需要更多的弱学习器的 迭代次数。 |
| 框架参数 | subsample | 子采样率,取值为(0,1],如果取值为 1,则全部样本都使用,等于没 有使用子采样。如果取值小于 1,则只有一部分样本会去做 GBDT 的 决策树拟合。选择小于 1 的比例可以减少方差,即防止过拟合,但是 会增加样本拟合的偏差,因此取值不能太低。 |
| 弱学习器参数 | max_features | 决策树划分时考虑的最大特征数,默认考虑全部特征,如果特征数非 常多,可以取部分特征,以控制决策树的生成时间。 |
| 弱学习器参数 | colsample_bytree | 构建树时的列抽样比例 |
| 弱学习器参数 | colsample_bylevel | 决策树每层分裂时的列抽样比例 |