周志华西瓜书学习笔记
间隔与支持向量
超平面 $(w, b)$,样本空间任意一点 $x$ 到超平面的距离公式:
$$r = \frac{|w^\top x + b|}{||w||}$$
分子表示点到超平面的有向距离,分母表示超平面法向量 $w$ 的范数(长度)。
对于二分类问题,给定一个训练样本集 $D ={ (x_1, y_1), (x_2, y_2), \dots, (x_m, y_m) }, y_i \in { -1, +1 }$. 假设超平面能够将训练样本正确分类,即对于 $(x _i, y _i) \in D$,若 $y_i=+1$,则有 $w ^\top x_i + b > 0$;反之则小于0. 令
$$w^\top x_i + b \geq +1, y_i = +1$$
$$w ^\top x_i + b \leq -1, y_i = -1$$
满足约束条件的距离超平面最近的这几个训练样本点被称为“支持向量” ;
两个边界之间的距离是 $\Gamma = \frac{2}{||w||}$,称为间隔。
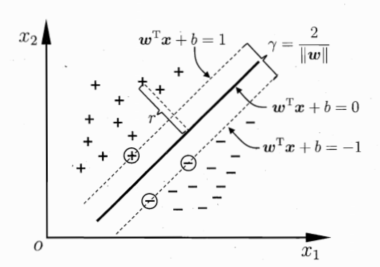
我们要做的事情是找到满足约束条件的 $w$ 和 $b$ 参数,使得对应的间隔最大来划分超平面,根据间隔公式,我们只需要最大化 $||w|| ^{-1}$,即最小化 $||w|| ^2$,即:
$$\min \limits _{w, b} \frac{1}{2} ||w|| ^2 \space$$
$$s.t. y_i(\omega ^\top x_i + b) \geq 1, i=1, 2, \dots, m.$$
使用拉格朗日乘子法得到其对偶问题,即为上述式子的每条约束添加拉格朗日乘子 $\alpha _i \geq 0$,则问题可以改写为:
$$L(\omega, b, \alpha) = \frac{1}{2} ||\omega|| ^2 + \sum \limits _{i=1} ^m \alpha _i (1-y _i(\omega ^\top x _i + b))$$
其中 $\alpha = (\alpha_1; \alpha _2; \dots ;\alpha _m)$,对 $\omega$ 和 $b$ 求偏导并令偏导为0,可得到:
$$\omega = \sum \limits _{i=1} ^m \alpha _i y_i x_i$$
$$0 = \sum \limits _{i=1} ^m \alpha _i y_i$$
将第一个式子代入拉格朗日函数消去w和b,再考虑第二个式子的约束条件,可得到原问题的对偶问题:
$$\max \limits _{\alpha} \sum \limits _{i=1} ^{m} \alpha _i - \frac{1}{2} \sum \limits _{i=1} ^{m} \sum \limits _{j=1} ^{m} \alpha _i \alpha _j y_i y_j x ^\top _{i} x_j$$
$$s.t. \sum \limits _{i=1} ^{m} \alpha _i y_i = 0, \alpha _i \geq 0, i = 1, 2, \dots, m.$$