数据结构-查找

算法查找

字数统计: 1.2k阅读时长: 4 min

 2021/04/15 

数据结构-查找

平均查找长度：一次查找的长度是指需要比较的关键字次数，平均查找长度则是所有查找过程中进行关键字的比较次数的平均值。

$$ASL = \sum \limits _ {i=1} ^ {n} P _i C _i$$

$n$是查找表的长度；$P _i$是查找第$i$个数据元素的概率；$C _i$是找到第$i$个数据元素所需进行的比较次数

查找表：

静态查找表：顺序查找、折半查找、散列查找；

动态查找表：二叉排序树的查找、散列查找。

顺序查找

一般线性表

线性表的第一个元素作为哨兵，作用是：哪怕该线性表没有命中查找元素最终也一定会在索引为0（即哨兵处）查找成功，代码可以简写成
1
for (int i = t.size() - 1; t[i] != key; --i) ;
这样就不必判断数组是否越界，若返回的索引值为0则直接就代表了查找失败。
对于一个有n个元素的线性表，给定一个key值与表中的第i个元素相等，需要进行 $n-i+1$ 次比较。即 $C_i = n-i+1$.查找成功时，平均查找长度为：

$$ASL _{success} = \sum \limits _{i=1} ^{n} P_i(n-i+1)$$

若每个元素的查找概率相等，即$P_i =\frac{1}{n}$时，则有：

$$ASL _{success} = \sum \limits _{i=1} ^{n} P _i(n-i+1) = \frac{n+1}{2}$$

若不存在就需要全扫一遍，因此：

$$ASL _{failure} = n + 1$$

有序线性表

解释一下下图。圆形结点表示有序线性表中存在的元素，如果用二叉树的结构来理解的话，10所在的层数为第一层，那么60在第六层；矩形结点表示失败结点，分别从第二层到第七层，第七层即最后一层有两个失败结点。

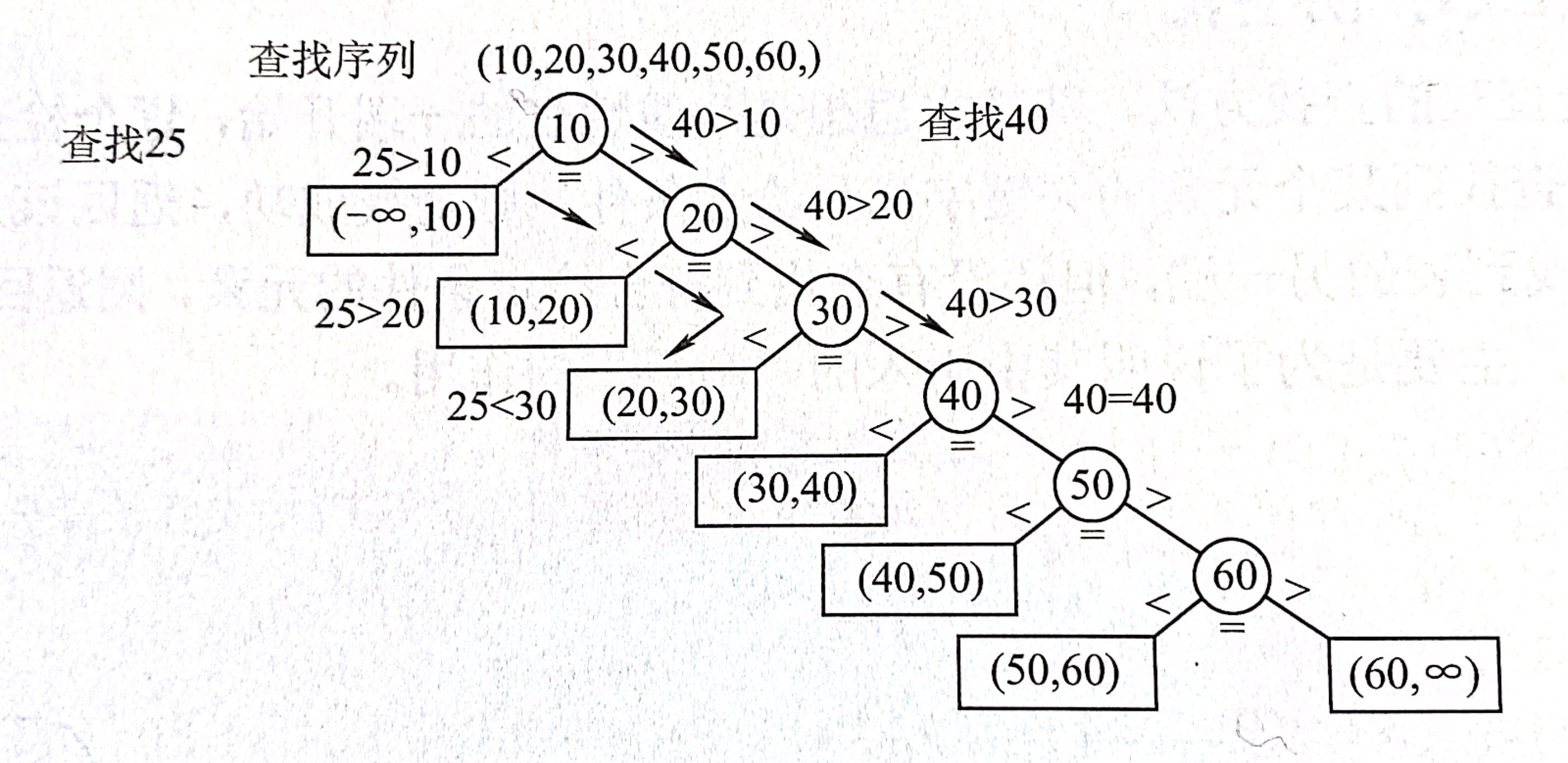
有序线性表的顺序查找成功的平均查找长度和一般情况相同；
失败的情况下略有不同，因为不用全扫一遍才能知道失败，上图的失败结点是虚构的，因此到达失败结点时所查找的长度等于他上面一个圆形结点所在的层数，因此分别是第一层到第六层和第六层。在查找概率相等的情况下，$q_j = \frac{1}{n+1}$，$l_j$是第$j$个失败结点所在的层数。

$$ASL _{failure} = \sum \limits _{j=1} ^{n} = q_j (l_i - 1) = \frac{1+2+…+n+n}{n+1} = \frac{n}{2} + \frac{n}{n+1}$$

二分/折半查找

老经典了，直接上模板。

// 非递归
int binary_search(vector<int> t, int key) {
  int low = 0, high = t.size() - 1, mid;
  while (low <= high) {
    mid = (low + high) / 2;
    if (t[mid] == key) {
      return mid;
    } else if (t[mid] > key) {
      high = mid - 1;
    } else {
      low = mid + 1;
    }
  }
  return -1;
}

// 递归
int binary_search(vector<int> t, int low, int high, int key) {
  if (low > high)	return -1;
  int mid = (low + high) / 2;
  if (t[mid] == key) {
    return mid;
  } else if (t[mid] > key) {
    return binary_search(t, low, mid - 1, key);
  } else {
    return binary_search(t, mid + 1, high, key);
  }
}

整个查找过程可以抽象成一颗二叉树，称为判定树，每个结点的值均大于其左子结点值，小于其右子结点值。若有序序列有n个元素，则对应的判定树有n个非叶结点和n+1个叶结点。而树的高度为$\lceil h = log_2(n+1) \rceil$

所以查找成功的平均查找长度为：

$$ASL_{success} = \frac{1}{n} \sum \limits _{i=1} ^{n} l _i = \frac{1}{n}(1 \times 2^{0}+2\times2^{1}+…+h \times 2^{h-1})$$

化简完为：

$$ASL_{success} = \frac{n+1}{n}log_2(n+1)-1 \approx log_2(n+1) - 1$$

时间复杂度为$O(log_2n)$，相比顺序查找更为高效

分块/索引顺序查找

将查找表分为若干个块，块内的元素可以无序，但是块间的元素是有序的，即第一个块中最大关键字需要小于第二个块中的最小关键字。建立一个索引表，记录每个块的最大关键字大小以及每个块的入口地址，索引表按照关键字的有序排列。

分块查找的平均长度为索引查找和块内查找的平均长度之和。设索引查找和块内查找的平均查找长度分别为$L_I, L_S$，则：

$$ASL_{success} = L_I + L_S$$

假设一共有$b$块，每块有$s$个记录record，等概率情况下，得：

$$ASL_{success} = L_I + L_S = \frac{b+1}{2} + \frac{s+1}{2} = \frac{s^2 + 2s + n}{2s}$$

树型查找

二叉排序树

平衡二叉树

红黑树

Next Post

机器学习-线性模型
Previous Post

虚拟机/服务器基础环境配置

CATALOG

1. 顺序查找
1. 1.1. 一般线性表
2. 1.2. 有序线性表
2. 二分/折半查找
3. 分块/索引顺序查找
4. 树型查找